Casimir invariant
Encyclopedia
In mathematics
, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra
of a Lie algebra
. A prototypical example is the squared angular momentum operator
, which is a Casimir invariant of the three-dimensional rotation group
.
The Casimir invariant is named after Hendrik Casimir
, who identified them in his description of rigid body dynamics in 1931.
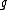is an 
-dimensional semisimple Lie algebra.
Let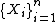
be any basis
of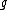
, and
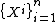
be the dual basis of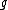
with respect to a fixed invariant bilinear form (e.g. the Killing form
) on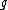
. The Casimir element 
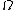is an element of the universal enveloping algebra 
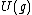given by the formula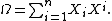
Although the definition of the Casimir element refers to a particular choice of basis in the Lie algebra, it is easy to show that the resulting element Ω is independent of this choice. Moreover, the invariance of the bilinear form used in the definition implies that the Casimir element commutes with all elements of the Lie algebra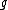
, and hence lies in the center of the universal enveloping algebra 
.
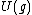Given any representation ρ of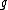
on a vector space V, possibly infinite-dimensional, the corresponding Casimir invariant is ρ(Ω), the linear operator on V given by the formula
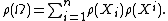
A special case of this construction plays an important role in differential geometry and global analysis. Suppose that a connected Lie group G with the Lie algebra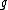
acts on a differentiable manifold M, then elements of 
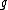are represented by first order differential operators on M. The representation ρ is on the space of smooth functions on M. In this situation the Casimir invariant is the G-invariant second order differential operator on M defined by the above formula.
More general Casimir invariants may also be defined, commonly occurring in the study of pseudo-differential operators in Fredholm theory.
of the universal enveloping algebra
of the Lie algebra. In other words, it is a member of the algebra of all differential operators that commutes with all the generators in the Lie algebra.
The number of independent elements of the center of the universal enveloping algebra is also the rank
in the case of a semisimple Lie algebra. The Casimir operator gives the concept of the Laplacian on a general semisimple Lie group; but this way of counting shows that there may be no unique analogue of the Laplacian, for rank > 1.
By definition any member of the center of the universal enveloping algebra commutes with all other elements in the algebra. By Schur's Lemma
, in any irreducible representation of the Lie algebra, the Casimir operator is thus proportional to the identity. This constant of proportionality can be used to classify the representations of the Lie algebra (and hence, also of its Lie group
). Physical mass and spin are examples of these constants, as are many other quantum number
s found in quantum mechanics
. Superficially, topological quantum number
s form an exception to this pattern; although deeper theories hint that these are two facets of the same phenomenon.
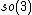is the Lie algebra of SO(3), the rotation group
for three-dimensional Euclidean space
. It is semisimple of rank 1, and so it has a single independent Casimir. The Killing form for the rotation group is just the Kronecker delta, and so the Casimir invariant is simply the sum of the squares of the generators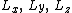
of the algebra. That is, the Casimir invariant is given by
In an irreducible representation, the invariance of the Casimir operator implies that it is a multiple of the identity element e of the algebra, so that
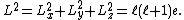
In quantum mechanics
, the scalar value
is referred to as the total angular momentum. For finite-dimensional matrix-valued representations
of the rotation group,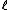
always takes on integer values (for bosonic representation
s) or half-integer values (for fermionic representation
s).
For a given value of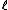
, the matrix representation is 
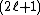-dimensional. Thus, for example, the three-dimensional representation for so(3) corresponds to 
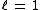, and is given by the generators
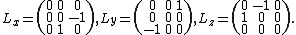
The quadratic Casimir invariant is then
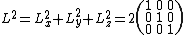
as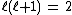
when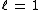 
. Similarly, the two dimensional representation has a basis given by the Pauli matrices
, which correspond to spin
1/2.
is central in the enveloping algebra, it acts on simple modules by a scalar. Let 
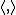be our favorite bilinear symmetric non-degenerate form, by which we define 
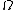. Let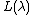 
be the finite dimensional highest weight module of weight 
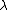. Then the Casimir element 
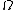acts on 
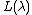by the constant 
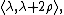where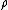 
is the weight defined by half the sum of the positive roots.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. A prototypical example is the squared angular momentum operator
Angular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
, which is a Casimir invariant of the three-dimensional rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
.
The Casimir invariant is named after Hendrik Casimir
Hendrik Casimir
Hendrik Brugt Gerhard Casimir FRS was a Dutch physicist best known for his research on the two-fluid model of superconductors in 1934 and the Casimir effect Hendrik Brugt Gerhard Casimir FRS (July 15, 1909 in The Hague, Netherlands – May 4, 2000 in Heeze) was a Dutch physicist best known...
, who identified them in his description of rigid body dynamics in 1931.
Definition
Suppose that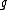 is an -dimensional semisimple Lie algebra.Let
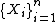
be any basis
Basis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
of
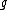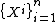
, andbe the dual basis of
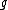with respect to a fixed invariant bilinear form (e.g. the Killing formKilling form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
) on
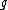. The Casimir element is an element of the universal enveloping algebra given by the formulaAlthough the definition of the Casimir element refers to a particular choice of basis in the Lie algebra, it is easy to show that the resulting element Ω is independent of this choice. Moreover, the invariance of the bilinear form used in the definition implies that the Casimir element commutes with all elements of the Lie algebra
, and hence lies in the center of the universal enveloping algebra 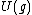.Given any representation ρ of
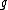on a vector space V, possibly infinite-dimensional, the corresponding Casimir invariant is ρ(Ω), the linear operator on V given by the formula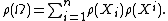A special case of this construction plays an important role in differential geometry and global analysis. Suppose that a connected Lie group G with the Lie algebra
acts on a differentiable manifold M, then elements of 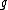are represented by first order differential operators on M. The representation ρ is on the space of smooth functions on M. In this situation the Casimir invariant is the G-invariant second order differential operator on M defined by the above formula.More general Casimir invariants may also be defined, commonly occurring in the study of pseudo-differential operators in Fredholm theory.
Properties
The Casimir operator is a distinguished element of the centerCenter (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of the Lie algebra. In other words, it is a member of the algebra of all differential operators that commutes with all the generators in the Lie algebra.
The number of independent elements of the center of the universal enveloping algebra is also the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
in the case of a semisimple Lie algebra. The Casimir operator gives the concept of the Laplacian on a general semisimple Lie group; but this way of counting shows that there may be no unique analogue of the Laplacian, for rank > 1.
By definition any member of the center of the universal enveloping algebra commutes with all other elements in the algebra. By Schur's Lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
, in any irreducible representation of the Lie algebra, the Casimir operator is thus proportional to the identity. This constant of proportionality can be used to classify the representations of the Lie algebra (and hence, also of its Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
). Physical mass and spin are examples of these constants, as are many other quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s found in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Superficially, topological quantum number
Topological quantum number
In physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...
s form an exception to this pattern; although deeper theories hint that these are two facets of the same phenomenon.
Example: so(3)
The Lie algebra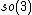 is the Lie algebra of SO(3), the rotation groupRotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
for three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. It is semisimple of rank 1, and so it has a single independent Casimir. The Killing form for the rotation group is just the Kronecker delta, and so the Casimir invariant is simply the sum of the squares of the generators
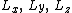of the algebra. That is, the Casimir invariant is given byIn an irreducible representation, the invariance of the Casimir operator implies that it is a multiple of the identity element e of the algebra, so that
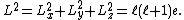
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the scalar value
is referred to as the total angular momentum. For finite-dimensional matrix-valued representationsGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the rotation group,
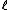always takes on integer values (for bosonic representationBoson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s) or half-integer values (for fermionic representation
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s).
For a given value of
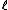, the matrix representation is 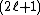-dimensional. Thus, for example, the three-dimensional representation for so(3) corresponds to 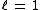, and is given by the generators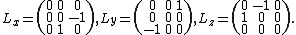The quadratic Casimir invariant is then
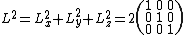
as
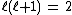when 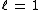. Similarly, the two dimensional representation has a basis given by the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
, which correspond to spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
1/2.
Eigenvalues
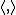Given that is central in the enveloping algebra, it acts on simple modules by a scalar. Let be our favorite bilinear symmetric non-degenerate form, by which we define 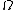. Let 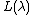be the finite dimensional highest weight module of weight 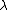. Then the Casimir element 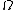acts on 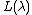by the constant 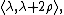where 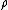is the weight defined by half the sum of the positive roots.