In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

, two square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

s, and one hexagon on each vertex

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

. It has Schläfli symbol of t_0,2{3, 6}.

Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

 calls it a rhombihexadeltille. It can be considered a cantellated or expanded

Expansion (geometry)

In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...

 hexagonal tiling by Johnson's operational language.

There are 3 regular and 8 semiregular tilings in the plane.

Uniform colorings

There is only one uniform coloring

Uniform coloring

In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...

 in a rhombitrihexagonal tiling. (Naming the colors by indices around a vertex (3.4.6.4): 1232.)

Related polyhedra and tilings

This tiling is topologically related as a part of sequence of cantellated

Cantellation (geometry)

In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...

 polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane

Hyperbolic space

In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...

. These vertex-transitive

Vertex-transitive

In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...

 figures have (*n32) reflectional symmetry.

(3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... (*332)	(3.4.4.4) Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... (*432)	(3.4.5.4) Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... (*532)
(3.4.6.4) (*632)	(3.4.7.4) (*732)	(3.4.8.4) (*832)

Gallery

An ornamental version

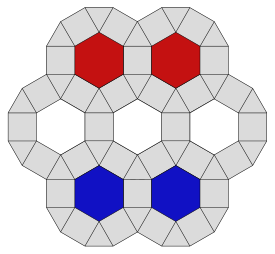The game Kensington Kensington (game) thumb|275px|Kensington game board illustration, showing [[rhombitrihexagonal tiling]]Kensington is a board game devised by Brian Taylor and Peter Forbes in 1979, named after an affluent borough of London...