
Supergroup (physics)
Encyclopedia
The concept of supergroup is a generalization
of that of group
. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them.
However the functions may have even and odd parts. Moreover a supergroup has a super Lie algebra which plays a role similar to that of a Lie algebra
for Lie groups in that they determine most of the representation theory and which is the starting point for classification.
More formally, a Lie supergroup is a supermanifold
G together with a multiplication morphism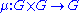 , an inversion morphism
, an inversion morphism 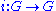 and a unit morphism
and a unit morphism  which makes G a group object
which makes G a group object
in the category
of supermanifolds. This means that, formulated as commutative diagrams, the usual associativity and inversion axioms of a group continue to hold. Since every manifold is a super manifold, a Lie supergroup generalises the notion of a Lie group
.
There are many possible supergroups. The ones of most interest in theoretical physics are the ones which extend the Poincaré group
or the conformal group
. Of particular interest are the orthosymplectic groups Osp(N/M) and the superconformal groups SU(N/M).
An equivalent algebraic approach starts from the observation that a super manifold is determined by its ring of supercommutative smooth functions, and that a morphism of super manifolds corresponds one to one with an algebra homomorphism between their functions in the opposite direction, i.e. that the category of supermanifolds is opposite to the category of algebras of smooth graded commutative functions. Reversing all the arrows in the commutative diagrams that define a Lie supergroup then shows that functions over the supergroup have the structure of a Z2-graded Hopf algebra
. Likewise the representations of this Hopf algebra turn out to be Z2-graded comodule
s. This Hopf algebra gives the global properties of the supergroup.
There is another related Hopf algebra which is the dual of the previous Hopf algebra. It can be identified with the Hopf algebra of graded differential operators at the origin. It only gives the local properties of the symmetries i.e., it only gives information about infinitesimal supersymmetry transformations. The representations of this Hopf algebra are module
s. Like in the non graded case, this Hopf algebra can be described purely algebraically as the universal enveloping algebra
of the Lie superalgebra
.
In a similar way one can define an affine algebraic supergroup as a group object in the category of super algebraic affine varieties. An affine algebraic supergroup has a similar one to one relation
to its Hopf algebra of super Polynomials. Using the language of schemes, which combines the geometric and algebraic point of view, algebraic supergroup schemes can be defined including super Abelian varieties.
Generalization
A generalization of a concept is an extension of the concept to less-specific criteria. It is a foundational element of logic and human reasoning. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements. As such, it...
of that of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them.
However the functions may have even and odd parts. Moreover a supergroup has a super Lie algebra which plays a role similar to that of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
for Lie groups in that they determine most of the representation theory and which is the starting point for classification.
More formally, a Lie supergroup is a supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
G together with a multiplication morphism
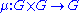 , an inversion morphism
, an inversion morphism 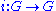 and a unit morphism
and a unit morphism  which makes G a group object
which makes G a group objectGroup object
In category theory, a branch of mathematics, group objects are certain generalizations of groups which are built on more complicated structures than sets...
in the category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of supermanifolds. This means that, formulated as commutative diagrams, the usual associativity and inversion axioms of a group continue to hold. Since every manifold is a super manifold, a Lie supergroup generalises the notion of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
There are many possible supergroups. The ones of most interest in theoretical physics are the ones which extend the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
or the conformal group
Conformal group
In mathematics, the conformal group is the group of transformations from a space to itself that preserve all angles within the space. More formally, it is the group of transformations that preserve the conformal geometry of the space. Several specific conformal groups are particularly important:*...
. Of particular interest are the orthosymplectic groups Osp(N/M) and the superconformal groups SU(N/M).
An equivalent algebraic approach starts from the observation that a super manifold is determined by its ring of supercommutative smooth functions, and that a morphism of super manifolds corresponds one to one with an algebra homomorphism between their functions in the opposite direction, i.e. that the category of supermanifolds is opposite to the category of algebras of smooth graded commutative functions. Reversing all the arrows in the commutative diagrams that define a Lie supergroup then shows that functions over the supergroup have the structure of a Z2-graded Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
. Likewise the representations of this Hopf algebra turn out to be Z2-graded comodule
Comodule
In mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.-Formal definition:...
s. This Hopf algebra gives the global properties of the supergroup.
There is another related Hopf algebra which is the dual of the previous Hopf algebra. It can be identified with the Hopf algebra of graded differential operators at the origin. It only gives the local properties of the symmetries i.e., it only gives information about infinitesimal supersymmetry transformations. The representations of this Hopf algebra are module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s. Like in the non graded case, this Hopf algebra can be described purely algebraically as the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of the Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
.
In a similar way one can define an affine algebraic supergroup as a group object in the category of super algebraic affine varieties. An affine algebraic supergroup has a similar one to one relation
to its Hopf algebra of super Polynomials. Using the language of schemes, which combines the geometric and algebraic point of view, algebraic supergroup schemes can be defined including super Abelian varieties.

