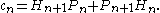Pell number
Encyclopedia
In mathematics
, the Pell numbers are an infinite sequence
of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2
. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell-Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82.
Both the Pell numbers and the companion Pell numbers may be calculated by means of a recurrence relation
similar to that for the Fibonacci number
s, and both sequences of numbers grow exponentially
, proportionally to powers of the silver ratio
1 + √2. As well as being used to approximate the square root of two, Pell numbers can be used to find square triangular number
s, to construct integer approximations to the right isosceles triangle, and to solve certain combinatorial enumeration problems.
As with Pell's equation
, the name of the Pell numbers stems from Leonhard Euler's
mistaken attribution of the equation and the numbers derived from it to John Pell
. The Pell-Lucas numbers are also named after Édouard Lucas
, who studied sequences defined by recurrences of this type; the Pell and companion Pell numbers are Lucas sequence
s.
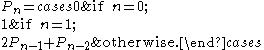
In words, the sequence of Pell numbers starts with 0 and 1, and then each Pell number is the sum of twice the previous Pell number and the Pell number before that. The first few terms of the sequence are
The Pell numbers can also be expressed by the closed form formula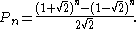
For large values of n, the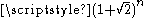 term dominates this expression, so the Pell numbers are approximately proportional to powers of the silver ratio
term dominates this expression, so the Pell numbers are approximately proportional to powers of the silver ratio
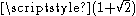 , analogous to the growth rate of Fibonacci numbers as powers of the golden ratio
, analogous to the growth rate of Fibonacci numbers as powers of the golden ratio
.
A third definition is possible, from the matrix
formula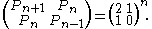
Many identities can be derived or proven from these definitions; for instance an identity analogous to Cassini's identity for Fibonacci numbers,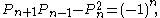
is an immediate consequence of the matrix formula (found by considering the determinant
s of the matrices on the left and right sides of the matrix formula).
 Pell numbers arise historically and most notably in the rational approximation
Pell numbers arise historically and most notably in the rational approximation
to the square root of 2
. If two large integers x and y form a solution to the Pell equation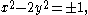
then their ratio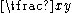 provides a close approximation to
provides a close approximation to 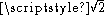 . The sequence of approximations of this form is
. The sequence of approximations of this form is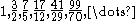
where the denominator of each fraction is a Pell number and the numerator is the sum of a Pell number and its predecessor in the sequence. That is, the solutions have the form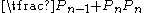 . The approximation
. The approximation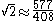
of this type was known to Indian mathematicians in the third or fourth century B.C. The Greek mathematicians of the fifth century B.C. also knew of this sequence of approximations; they called the denominators and numerators of this sequence side and diameter numbers and the numerators were also known as rational diagonals or rational diameters.
These approximations can be derived from the continued fraction
expansion of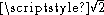 :
: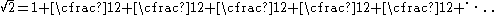
Truncating this expansion to any number of terms produces one of the Pell-number-based approximations in this sequence; for instance,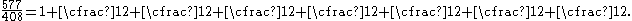
As Knuth (1994) describes, the fact that Pell numbers approximate allows them to be used for accurate rational approximations to a regular octagon with vertex coordinates
allows them to be used for accurate rational approximations to a regular octagon with vertex coordinates 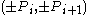 and
and 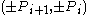 . All vertices are equally distant from the origin, and form nearly uniform angles around the origin. Alternatively, the points
. All vertices are equally distant from the origin, and form nearly uniform angles around the origin. Alternatively, the points 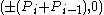 ,
, 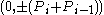 , and
, and 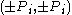 form approximate octagons in which the vertices are nearly equally distant from the origin and form uniform angles.
form approximate octagons in which the vertices are nearly equally distant from the origin and form uniform angles.
. The first few Pell primes are
As with the Fibonacci numbers, a Pell number can only be prime if n itself is prime.
can only be prime if n itself is prime.
The only Pell numbers that are squares, cubes, or any higher power of an integer are 0, 1, and 169 = 132.
However, despite having so few squares or other powers, Pell numbers have a close connection to square triangular number
s. Specifically, these numbers arise from the following identity of Pell numbers: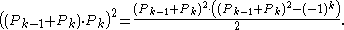
The left side of this identity describes a square number
, while the right side describes a triangular number
, so the result is a square triangular number.
Santana and Diaz-Barrero (2006) prove another identity relating Pell numbers to squares and showing that the sum of the Pell numbers up to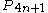 is always a square:
is always a square: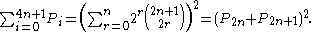
For instance, the sum of the Pell numbers up to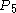 ,
, 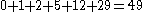 , is the square of
, is the square of 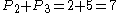 . The numbers
. The numbers 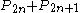 forming the square roots of these sums,
forming the square roots of these sums,
are known as the Newman–Shanks–Williams (NSW) numbers.
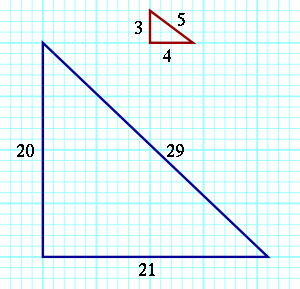 If a right triangle
If a right triangle
has integer side lengths a, b, c (necessarily satisfying the Pythagorean theorem
a2+b2=c2), then (a,b,c) is known as a Pythagorean triple
. As Martin (1875) describes, the Pell numbers can be used to form Pythagorean triples in which a and b are one unit apart, corresponding to right triangles that are nearly isosceles. Each such triple has the form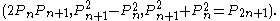
The sequence of Pythagorean triples formed in this way is, (20,21,29), (120,119,169), (696,697,985), ....
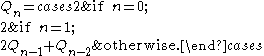
In words: the first two numbers in the sequence are both 2, and each successive number is formed by adding twice the previous Pell-Lucas number to the Pell-Lucas number before that, or equivalently, by adding the next Pell number to the previous Pell number: thus, 82 is the companion to 29, and 82 = 2 * 34 + 14 = 70 + 12. The first few terms of the sequence are : 2, 2, 6, 14
, 34
, 82
, 198
, 478...
The companion Pell numbers can be expressed by the closed form formula
These numbers are all even; each such number is twice the numerator in one of the rational approximations to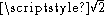 discussed above.
discussed above.
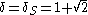 and its conjugate
and its conjugate 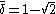 .
.
The coefficients are the Half companion Pell numbers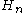 and The Pell numbers
and The Pell numbers 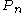 which are the (non-negative) solutions to
which are the (non-negative) solutions to
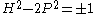 . A Square triangular number
. A Square triangular number
is a number which is both the
which is both the  th triangular number and the
th triangular number and the  th square number. A near isosceles Pythagorean triple is an integer solution to
th square number. A near isosceles Pythagorean triple is an integer solution to 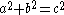 where
where  .
.
The next table shows that splitting the odd number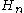 into nearly equal halves gives a square triangular number when n is even and a near isosceles Pythagorean triple when n is odd. All solutions arise in this manner.
into nearly equal halves gives a square triangular number when n is even and a near isosceles Pythagorean triple when n is odd. All solutions arise in this manner.
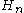 and the Pell numbers
and the Pell numbers 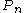
can be derived in a number of easily equivalent ways:
Raising to powers:
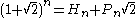
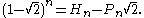
From this it follows that there are closed forms:
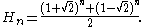
and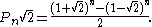
Paired recurrences:
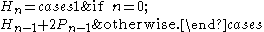

and matrix formulations:
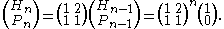
So
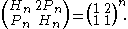
 and
and  is
is 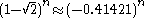 which goes rapidly to zero. So
which goes rapidly to zero. So
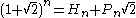 is extremely close
is extremely close  .
.
From this last observation it follows that the integer ratios rapidly approach
rapidly approach 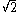 while
while 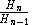 and
and 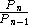 rapidly approach
rapidly approach 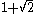 .
.
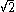 is irrational, we can't have
is irrational, we can't have 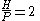 i.e.
i.e. 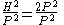 . The best we can achieve is either
. The best we can achieve is either 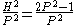 or
or 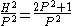 .
.
The (non-negative) solutions to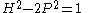 are exactly the pairs
are exactly the pairs  even and the solutions to
even and the solutions to 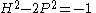 are exactly the pairs
are exactly the pairs  odd. To see this, note first that
odd. To see this, note first that
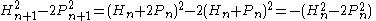
so that these differences, starting with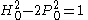 are alternately
are alternately
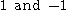 . Then note that every positive solution comes in this way from a solution with smaller integers since
. Then note that every positive solution comes in this way from a solution with smaller integers since
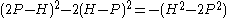 . The smaller solution also has positive integers with the one exception
. The smaller solution also has positive integers with the one exception
 which comes from
which comes from 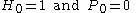 .
.
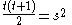 is equivalent to
is equivalent to 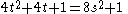 which becomes
which becomes
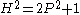 with the substitutions
with the substitutions 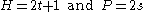 . Hence the nth solution is
. Hence the nth solution is 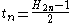 and
and 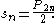
Observe that and
and 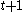 are relatively prime so that
are relatively prime so that 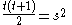 happens exactly when they are adjacent integers, one a square
happens exactly when they are adjacent integers, one a square  and the other twice a square
and the other twice a square 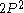 . Since we know all solutions of that equation, we also have
. Since we know all solutions of that equation, we also have
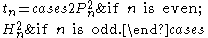
and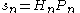
This alternate expression is seen in the next table.
 occurs exactly when
occurs exactly when 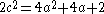 which becomes
which becomes 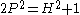 with the substitutions
with the substitutions
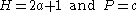 . Hence the nth solution is
. Hence the nth solution is 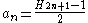 and
and 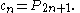
The table above shows that, in one order or the other,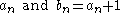 are
are 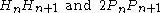 while
while 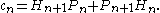
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Pell numbers are an infinite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell-Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82.
Both the Pell numbers and the companion Pell numbers may be calculated by means of a recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
similar to that for the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s, and both sequences of numbers grow exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
, proportionally to powers of the silver ratio
Silver ratio
In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
1 + √2. As well as being used to approximate the square root of two, Pell numbers can be used to find square triangular number
Square triangular number
In mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
s, to construct integer approximations to the right isosceles triangle, and to solve certain combinatorial enumeration problems.
As with Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
, the name of the Pell numbers stems from Leonhard Euler's
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
mistaken attribution of the equation and the numbers derived from it to John Pell
John Pell
-Early life:He was born at Southwick in Sussex. He was educated at Steyning Grammar School, and entered Trinity College, Cambridge, at the age of thirteen. During his university career he became an accomplished linguist, and even before he took his B.A. degree corresponded with Henry Briggs and...
. The Pell-Lucas numbers are also named after Édouard Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
, who studied sequences defined by recurrences of this type; the Pell and companion Pell numbers are Lucas sequence
Lucas sequence
In mathematics, the Lucas sequences Un and Vn are certain integer sequences that satisfy the recurrence relationwhere P and Q are fixed integers...
s.
Pell numbers
The Pell numbers are defined by the recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
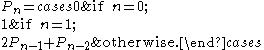
In words, the sequence of Pell numbers starts with 0 and 1, and then each Pell number is the sum of twice the previous Pell number and the Pell number before that. The first few terms of the sequence are
- , 1, 2, 5, 1212 (number)12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten...
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, 7070 (number)70 is the natural number following 69 and preceding 71.-In mathematics:Its factorization makes it a sphenic number. 70 is a Pell number and a generalized heptagonal number, one of only two numbers to be both. Also, it is the seventh pentagonal number and the fourth 13-gonal number, as well as the...
, 169169 (number)169 is the natural number following 168 and preceding 170.-In mathematics:* 169 is an odd number* 169 is a square number. 13 x 13 = 169, and the reverse 31 x 31 = 961...
, 408, 985, 2378... .
The Pell numbers can also be expressed by the closed form formula
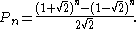
For large values of n, the
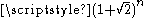 term dominates this expression, so the Pell numbers are approximately proportional to powers of the silver ratio
term dominates this expression, so the Pell numbers are approximately proportional to powers of the silver ratioSilver ratio
In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
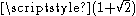 , analogous to the growth rate of Fibonacci numbers as powers of the golden ratio
, analogous to the growth rate of Fibonacci numbers as powers of the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
A third definition is possible, from the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
formula
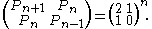
Many identities can be derived or proven from these definitions; for instance an identity analogous to Cassini's identity for Fibonacci numbers,
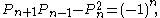
is an immediate consequence of the matrix formula (found by considering the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s of the matrices on the left and right sides of the matrix formula).
Approximation to the square root of two

Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
to the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
. If two large integers x and y form a solution to the Pell equation
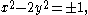
then their ratio
 provides a close approximation to
provides a close approximation to  . The sequence of approximations of this form is
. The sequence of approximations of this form is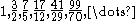
where the denominator of each fraction is a Pell number and the numerator is the sum of a Pell number and its predecessor in the sequence. That is, the solutions have the form
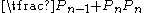 . The approximation
. The approximation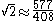
of this type was known to Indian mathematicians in the third or fourth century B.C. The Greek mathematicians of the fifth century B.C. also knew of this sequence of approximations; they called the denominators and numerators of this sequence side and diameter numbers and the numerators were also known as rational diagonals or rational diameters.
These approximations can be derived from the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion of
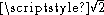 :
: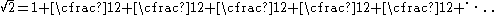
Truncating this expansion to any number of terms produces one of the Pell-number-based approximations in this sequence; for instance,
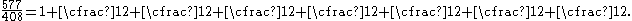
As Knuth (1994) describes, the fact that Pell numbers approximate
 allows them to be used for accurate rational approximations to a regular octagon with vertex coordinates
allows them to be used for accurate rational approximations to a regular octagon with vertex coordinates  and
and  . All vertices are equally distant from the origin, and form nearly uniform angles around the origin. Alternatively, the points
. All vertices are equally distant from the origin, and form nearly uniform angles around the origin. Alternatively, the points 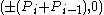 ,
, 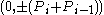 , and
, and 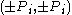 form approximate octagons in which the vertices are nearly equally distant from the origin and form uniform angles.
form approximate octagons in which the vertices are nearly equally distant from the origin and form uniform angles.Primes and squares
A Pell prime is a Pell number that is primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. The first few Pell primes are
- 2, 5, 29, 5741, ... .
As with the Fibonacci numbers, a Pell number
 can only be prime if n itself is prime.
can only be prime if n itself is prime.The only Pell numbers that are squares, cubes, or any higher power of an integer are 0, 1, and 169 = 132.
However, despite having so few squares or other powers, Pell numbers have a close connection to square triangular number
Square triangular number
In mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
s. Specifically, these numbers arise from the following identity of Pell numbers:
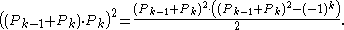
The left side of this identity describes a square number
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, while the right side describes a triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
, so the result is a square triangular number.
Santana and Diaz-Barrero (2006) prove another identity relating Pell numbers to squares and showing that the sum of the Pell numbers up to
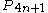 is always a square:
is always a square: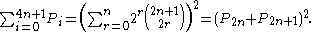
For instance, the sum of the Pell numbers up to
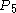 ,
, 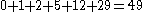 , is the square of
, is the square of 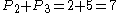 . The numbers
. The numbers 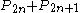 forming the square roots of these sums,
forming the square roots of these sums,
- 1, 7, 41, 239, 1393, 8119, 47321, ... ,
are known as the Newman–Shanks–Williams (NSW) numbers.
Pythagorean triples

Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
has integer side lengths a, b, c (necessarily satisfying the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
a2+b2=c2), then (a,b,c) is known as a Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
. As Martin (1875) describes, the Pell numbers can be used to form Pythagorean triples in which a and b are one unit apart, corresponding to right triangles that are nearly isosceles. Each such triple has the form
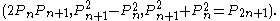
The sequence of Pythagorean triples formed in this way is, (20,21,29), (120,119,169), (696,697,985), ....
Pell-Lucas numbers
The companion Pell numbers or Pell-Lucas numbers are defined by the recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
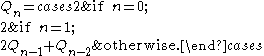
In words: the first two numbers in the sequence are both 2, and each successive number is formed by adding twice the previous Pell-Lucas number to the Pell-Lucas number before that, or equivalently, by adding the next Pell number to the previous Pell number: thus, 82 is the companion to 29, and 82 = 2 * 34 + 14 = 70 + 12. The first few terms of the sequence are : 2, 2, 6, 14
14 (number)
14 is the natural number following 13 and preceding 15.In speech, the numbers 14 and 40 are often confused. When carefully enunciated, they differ in which syllable is stressed: 14 vs 40...
, 34
34 (number)
34 is the natural number following 33 and preceding 35.-In mathematics:34 is the ninth distinct semiprime and has four divisors including unity and itself. Its neighbors, 33 and 35, also are distinct semiprimes, having four divisors each, and 34 is the smallest number to be surrounded by numbers...
, 82
82 (number)
82 is the natural number following 81 and preceding 83.-In mathematics:Eighty-two is the twenty-third biprime and the twelfth of the form...
, 198
198 (number)
198 is the natural number following 197 and preceding 199.-In mathematics:* 198 is an even number* 198 is an abundant number, as 270 is greater than 198* 198 is a composite number* 198 is a Harshad number, divisible by the sum of its digits...
, 478...
The companion Pell numbers can be expressed by the closed form formula

These numbers are all even; each such number is twice the numerator in one of the rational approximations to
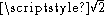 discussed above.
discussed above.Computations and connections
The following table gives the first few powers of the silver ratioSilver ratio
In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
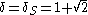 and its conjugate
and its conjugate 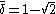 .
.
 |
 |
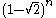 |
|---|---|---|
| 0 | 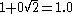 |
 |
| 1 | 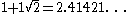 |
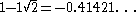 |
| 2 | 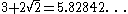 |
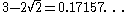 |
| 3 | 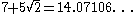 |
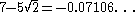 |
| 4 | 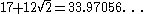 |
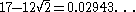 |
| 5 | 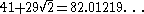 |
 |
| 6 | 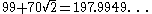 |
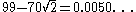 |
| 7 | 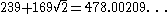 |
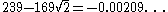 |
| 8 |  |
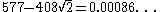 |
| 9 | 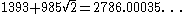 |
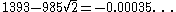 |
| 10 | 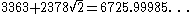 |
 |
| 11 | 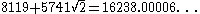 |
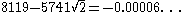 |
| 12 | 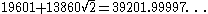 |
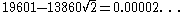 |
The coefficients are the Half companion Pell numbers
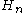 and The Pell numbers
and The Pell numbers 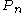 which are the (non-negative) solutions to
which are the (non-negative) solutions to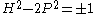 . A Square triangular number
. A Square triangular numberSquare triangular number
In mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
is a number
 which is both the
which is both the  th triangular number and the
th triangular number and the 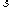 th square number. A near isosceles Pythagorean triple is an integer solution to
th square number. A near isosceles Pythagorean triple is an integer solution to 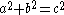 where
where 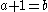 .
.The next table shows that splitting the odd number
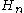 into nearly equal halves gives a square triangular number when n is even and a near isosceles Pythagorean triple when n is odd. All solutions arise in this manner.
into nearly equal halves gives a square triangular number when n is even and a near isosceles Pythagorean triple when n is odd. All solutions arise in this manner.  |
 |
 |
t | t+1 | s | a | b | c |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | |||
| 1 | 1 | 1 | 0 | 1 | 1 | |||
| 2 | 3 | 2 | 1 | 2 | 1 | |||
| 3 | 7 | 5 | 3 | 4 | 5 | |||
| 4 | 17 | 12 | 8 | 9 | 6 | |||
| 5 | 41 | 29 | 20 | 21 | 29 | |||
| 6 | 99 | 70 | 49 | 50 | 35 | |||
| 7 | 239 | 169 | 119 | 120 | 169 | |||
| 8 | 577 | 408 | 288 | 289 | 204 | |||
| 9 | 1393 | 985 | 696 | 697 | 985 | |||
| 10 | 3363 | 2378 | 1681 | 1682 | 1189 | |||
| 11 | 8119 | 5741 | 4059 | 4060 | 5741 | |||
| 12 | 19601 | 13860 | 9800 | 9801 | 6930 |
Definitions
The half companion Pell Numbers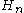 and the Pell numbers
and the Pell numbers 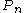
can be derived in a number of easily equivalent ways:
Raising to powers:
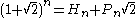
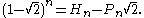
From this it follows that there are closed forms:
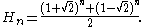
and
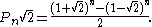
Paired recurrences:
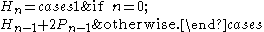

and matrix formulations:
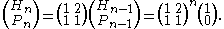
So
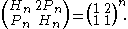
Approximations
The difference between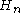 and
and 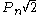 is
is 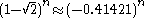 which goes rapidly to zero. So
which goes rapidly to zero. So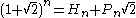 is extremely close
is extremely close 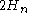 .
.From this last observation it follows that the integer ratios
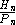 rapidly approach
rapidly approach 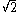 while
while 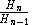 and
and 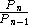 rapidly approach
rapidly approach 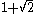 .
.H2 − 2P2 = ±1
Since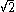 is irrational, we can't have
is irrational, we can't have 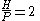 i.e.
i.e. 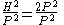 . The best we can achieve is either
. The best we can achieve is either 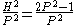 or
or 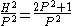 .
.The (non-negative) solutions to
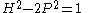 are exactly the pairs
are exactly the pairs  even and the solutions to
even and the solutions to 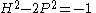 are exactly the pairs
are exactly the pairs  odd. To see this, note first that
odd. To see this, note first that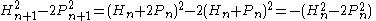
so that these differences, starting with
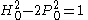 are alternately
are alternately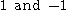 . Then note that every positive solution comes in this way from a solution with smaller integers since
. Then note that every positive solution comes in this way from a solution with smaller integers since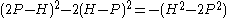 . The smaller solution also has positive integers with the one exception
. The smaller solution also has positive integers with the one exception which comes from
which comes from 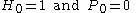 .
.Square triangular numbers
The required equation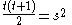 is equivalent to
is equivalent to 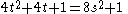 which becomes
which becomes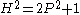 with the substitutions
with the substitutions 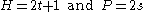 . Hence the nth solution is
. Hence the nth solution is 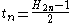 and
and 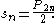
Observe that
 and
and 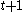 are relatively prime so that
are relatively prime so that 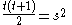 happens exactly when they are adjacent integers, one a square
happens exactly when they are adjacent integers, one a square  and the other twice a square
and the other twice a square 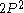 . Since we know all solutions of that equation, we also have
. Since we know all solutions of that equation, we also have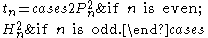
and
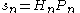
This alternate expression is seen in the next table.
 |
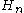 |
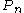 |
t | t+1 | s | a | b | c | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | ||||||||
| 1 | 1 | 1 | 1 | 2 | 1 | 1 | 0 | 1 | ||
| 2 | 3 | 2 | 8 | 9 | 6 | 3 | 4 | 5 | ||
| 3 | 7 | 5 | 49 | 50 | 35 | 21 | 20 | 29 | ||
| 4 | 17 | 12 | 288 | 289 | 204 | 119 | 120 | 169 | ||
| 5 | 41 | 29 | 1681 | 1682 | 1189 | 697 | 696 | 985 | ||
| 6 | 99 | 70 | 9800 | 9801 | 6930 | 4059 | 4060 | 5741 |
Pythagorean triples
The equality occurs exactly when
occurs exactly when 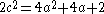 which becomes
which becomes 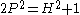 with the substitutions
with the substitutions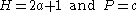 . Hence the nth solution is
. Hence the nth solution is 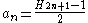 and
and 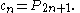
The table above shows that, in one order or the other,
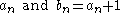 are
are 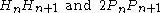 while
while