Errett Bishop
Encyclopedia
Errett Albert Bishop was an American
mathematician
known for his work on analysis. He is the father of constructive analysis, because of his 1967 Foundations of Constructive Analysis, where he proved
most of the important theorem
s in real analysis
by constructive
methods.
at West Point, ending his career as professor of mathematics at Wichita State University
in Kansas. Although he died when Errett was only 5 years old, he influenced Errett's eventual career by the math texts he left behind, which is how Errett discovered mathematics. Errett grew up in Newton, Kansas
. He and his sister were apparent math prodigies.
Bishop entered the University of Chicago
in 1944, obtaining both the BS and MS in 1947. The doctoral studies he began in that year were interrupted by two years in the US Army, 1950–52, doing mathematical research at the National Bureau of Standards. He completed his Ph.D. in 1954 under Paul Halmos
; his thesis was titled Spectral Theory for Operations on Banach Spaces.
Bishop taught at the University of California
, 1954–65. He spent the 1964–65 academic year at the Miller Institute for Basic Research in Berkeley
. From 1965 until his death, he was professor at the University of California at San Diego.
In 1972, Bishop (with Henry Cheng) published Constructive Measure Theory.
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
known for his work on analysis. He is the father of constructive analysis, because of his 1967 Foundations of Constructive Analysis, where he proved
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
most of the important theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
by constructive
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
methods.
Life
Errett Bishop's father, Albert T Bishop, graduated from the United States Military AcademyUnited States Military Academy
The United States Military Academy at West Point is a four-year coeducational federal service academy located at West Point, New York. The academy sits on scenic high ground overlooking the Hudson River, north of New York City...
at West Point, ending his career as professor of mathematics at Wichita State University
Wichita State University
Wichita State University is a NCAA Division I public university in Wichita, Kansas with selective admissions. WSU is one of six state universities governed by the Kansas Board of Regents. The current president is Dr. Donald Beggs....
in Kansas. Although he died when Errett was only 5 years old, he influenced Errett's eventual career by the math texts he left behind, which is how Errett discovered mathematics. Errett grew up in Newton, Kansas
Newton, Kansas
Newton is a city in and the county seat of Harvey County, Kansas, United States. As of the 2010 census, the city population was 19,132. Newton is located north of Wichita and is included in the Wichita metropolitan statistical area...
. He and his sister were apparent math prodigies.
Bishop entered the University of Chicago
University of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
in 1944, obtaining both the BS and MS in 1947. The doctoral studies he began in that year were interrupted by two years in the US Army, 1950–52, doing mathematical research at the National Bureau of Standards. He completed his Ph.D. in 1954 under Paul Halmos
Paul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
; his thesis was titled Spectral Theory for Operations on Banach Spaces.
Bishop taught at the University of California
University of California
The University of California is a public university system in the U.S. state of California. Under the California Master Plan for Higher Education, the University of California is a part of the state's three-tier public higher education system, which also includes the California State University...
, 1954–65. He spent the 1964–65 academic year at the Miller Institute for Basic Research in Berkeley
Berkeley, California
Berkeley is a city on the east shore of the San Francisco Bay in Northern California, United States. Its neighbors to the south are the cities of Oakland and Emeryville. To the north is the city of Albany and the unincorporated community of Kensington...
. From 1965 until his death, he was professor at the University of California at San Diego.
Work
Bishop's wide-ranging work falls into five categories:- Polynomial and rational approximation. Examples are extensions of Mergelyan's approximation theorem and the theorem of Frigyes RieszFrigyes RieszFrigyes Riesz was a mathematician who was born in Győr, Hungary and died in Budapest, Hungary. He was rector and professor at University of Szeged...
and Marcel RieszMarcel RieszMarcel Riesz was a Hungarian mathematician who was born in Győr, Hungary . He moved to Sweden in 1908 and spent the rest of his life there, dying in Lund, where he was a professor from 1926 at Lund University...
concerning measures on the unit circle orthogonal to polynomials. - The general theory of function algebras. Here Bishop worked on uniform algebraUniform algebraA uniform algebra A on a compact Hausdorff topological space X is a closed subalgebra of the C*-algebra C with the following properties:As a closed subalgebra of the commutative Banach algebra C a uniform algebra is itself a unital commutative Banach algebra A uniform algebra A on a compact...
s (commutative Banach algebraBanach algebraIn mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s with unit whose norms are the spectral norms) proving results such as antisymmetric decomposition of a uniform algebra, the Bishop-DeLeeuw theorem, and the proof of existence of Jensen measures. Bishop wrote a 1965 survey "Uniform algebras," examining the interaction between the theory of uniform algebras and that of several complex variables. - Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s and operator theoryOperator theoryIn mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, the subject of his thesis. He introduced what is now called the Bishop condition, useful in the theory of decomposable operators. - The theory of functions of several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. An example is his 1962 "Analyticity in certain Banach spaces." He proved important results in this area such as the biholomorphic embedding theorem for a Stein manifoldStein manifoldIn mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
as a closed submanifoldSubmanifoldIn mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
in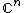
, and a new proof of RemmertReinhold RemmertReinhold Remmert is a German mathematician born in Osnabrück, Germany. He studied mathematics, mathematical logic and physics in Münster. He established and developed the theory of complex spaces in joint work with Hans Grauert...
's proper mapping theorem. - Constructive mathematics. Bishop become interested in foundational issues while at the Miller Institute. His now-famous Foundations of Constructive Analysis (1967) aimed to show that a constructive treatment of analysis is feasible, something about which WeylHermann WeylHermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
had been pessimistic. A 1985 revision, called Constructive Analysis, was completed with the assistance of Douglas Bridges.
In 1972, Bishop (with Henry Cheng) published Constructive Measure Theory.
Quotes
- (A) "Mathematics is common sense";
- (B) "Do not ask whether a statement is true until you know what it means";
- (C) "A proof is any completely convincing argument";
- (D) "Meaningful distinctions deserve to be preserved".
- "The primary concern of mathematics is number, and this means the positive integers. . . . In the words of Kronecker, the positive integers were created by God. Kronecker would have expressed it even better if he had said that the positive integers were created by God for the benefit of man (and other finite beings). Mathematics belongs to man, not to God. We are not interested in properties of the positive integers that have no descriptive meaning for finite man. When a man proves a positive integer to exist, he should show how to find it. If God has mathematics of his own that needs to be done, let him do it himself." (Bishop 1967, Chapter 1, A Constructivist Manifesto, page 2)
- "We are not contending that idealistic mathematics is worthless from the constructive point of view. This would be as silly as contending that unrigorous mathematics is worthless from the classical point of view. Every theorem proved with idealistic methods presents a challenge: to find a constructive version, and to give it a constructive proof." (Bishop 1967, Preface, page x)
- "Theorem 1 is the famous theorem of Cantor, that the real numbers are uncountable. The proof is essentially Cantor's 'diagonal' proof. Both Cantor's theorem and his method of proof are of great importance." (Bishop 1967, Chapter 2, Calculus and the Real Numbers, page 25)
- "The real numbers, for certain purposes, are too thin. Many beautiful phenomena become fully visible only when the complex numbers are brought to the fore." (Bishop 1967, Chapter 5, Complex Analysis, page 113)
- "It is clear that many of the results in this book could be programmed for a computer, by some such procedure as that indicated above. In particular, it is likely that most of the results of Chaps. 2, 4, 5, 9, 10, and 11 could be presented as computer programs. As an example, a complete separable metric space X can be described by a sequence of real numbers, and therefore by a sequence of integers, simply by listing the distances between each pair of elements of a given countable dense set. . . . As written, this book is person-oriented rather than computer-oriented. It would be of great interest to have a computer-oriented version." (Bishop 1967, Appendix B, Aspects of Constructive Truth, pages 356 and 357)
- "Very possibly classical mathematics will cease to exist as an independent discipline” (Bishop, 1970, p. 54)
- “Brouwer’s criticisms of classical mathematics were concerned with what I shall refer to as ‘the debasement of meaning’ ” (Bishop in Rosenblatt, 1985, p. 1)
See also
- Constructive analysis
- Constructivism (mathematics)Constructivism (mathematics)In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
- Criticism of non-standard analysisCriticism of non-standard analysisNon-standard analysis and its offshoot, non-standard calculus, have been criticized by several authors. The evaluation of non-standard analysis in the literature has varied greatly...