Spin network - AbsoluteAstronomy.com

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, a spin network is a type of diagram which can be used to represent states and interactions between particles

Particle physics

Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...

and fields

Quantum field theory

Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...

in quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

. From a mathematical perspective, the diagrams are a concise way to represent multilinear functions and functions between representations

Representation theory

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...

of matrix group

Matrix group

In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...

s. The diagrammatic notation often simplifies calculation because simple diagrams may be used to represent complicated functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

. Roger Penrose

Roger Penrose

Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...

is credited with the invention of spin networks in 1971, although similar diagrammatic techniques existed before that time.

Spin networks have been applied to the theory of quantum gravity

Quantum gravity

Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...

by Carlo Rovelli

Carlo Rovelli

Carlo Rovelli is an Italian physicist who has worked in Italy, the USA, and France. His work is mainly in the field of quantum gravity. He is among the founders of the Loop Quantum Gravity theory.-Life and career:...

, Lee Smolin

Lee Smolin

Lee Smolin is an American theoretical physicist, a researcher at the Perimeter Institute for Theoretical Physics, and an adjunct professor of physics at the University of Waterloo. He is married to Dina Graser, a communications lawyer in Toronto. His brother is David M...

, Jorge Pullin

Jorge Pullin

Jorge Pullin is the Horace Hearne Chair in theoretical Physics at the Louisiana State University, known for his work on black hole collisions and quantum gravity.-Biography:...

and others. They can also be used to construct a particular functional

Functional (mathematics)

In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...

on the space of connections

Connection (mathematics)

In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...

which is invariant under local gauge transformations.

Penrose's original definition

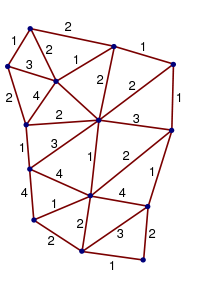
A spin network, as described in Penrose 1971, is a kind of diagram in which each line segment represents the world line

World line

In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...

of a "unit" (either an elementary particle

Elementary particle

In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...

or a compound system of particles). Three line segments join at each vertex. A vertex may be interpreted as an event in which either a single unit splits into two or two units collide and join into a single unit. Diagrams whose line segments are all joined at vertices are called closed spin networks. Time may be viewed as going in one direction, such as from the bottom to the top of the diagram, but for closed spin networks the direction of time is irrelevant to calculations.

Each line segment is labeled with an integer called a spin number. A unit with spin number n is called an n-unit and has angular momentum

Angular momentum

In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...

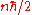, where

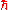is the reduced Planck constant

Planck constant

The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...

. For boson

Boson

In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....

s, such as photon

Photon

In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...

s and gluon

Gluon

Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....

s, n is an even number. For fermion

Fermion

In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....

s, such as electron

Electron

The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...

s and quark

Quark

A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...

s, n is odd.

Given any closed spin network, a non-negative integer can be calculated which is called the norm of the spin network. Norms can be used to calculate the probabilities of various spin values. A network whose norm is zero has zero probability of occurrence. The rules for calculating norms and probabilities are beyond the scope of this article. However, they imply that for a spin network to have nonzero norm, two requirements must be met at each vertex. Suppose a vertex joins three units with spin numbers a, b, and c. Then, these requirements are stated as:

Triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....

: a must be less than or equal to b+c, b less than or equal to a+c, and c less than or equal to a+b.
Fermion conservation: a+b+c must be an even number.

For example, a=3, b=4, c=6 is impossible since 3+4+6=13 is odd, and a=3, b=4, c=9 is impossible since 3+4<9. However, a=3, b=4, c=5 is possible since 3+4+5=12 is even and the triangle inequality is satisfied.
Some conventions use labellings by half-integers, with the condition that the sum a+b+c must be a whole number.

Formal definition

More formally, a spin network is a (directed) graph

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

whose edges

Graph theory

are associated with irreducible representations of a compact

Compact group

In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

and whose vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

are associated with intertwiners of the edge representations adjacent to it.

A spin network, immersed into a manifold, can be used to define a functional

Functional (mathematics)

on the space of connections on this manifold. One computes holonomies

Holonomy

In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...

of the connection along every link of the graph, determines representation matrices corresponding to every link, multiplies all matrices and intertwiners together, and contracts indices in a prescribed way. A remarkable feature of the resulting functional is that it is invariant under local gauge transformations.

In the context of loop quantum gravity

In loop quantum gravity

Loop quantum gravity

Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...

(LQG), a spin network represents a "quantum state" of the gravitational field

Gravitational field

The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...

on a 3-dimensional hypersurface

Hypersurface

In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...

. The set of all possible spin networks (or, more accurately, "s-knot

S-knot

In loop quantum gravity, an s-knot is an equivalence class of spin networks under diffeomorphisms. In this formalism, s-knots represent the quantum states of the gravitational field.- External links :* Living Reviews in Relativity:...

s" - that is, equivalence classes of spin networks under diffeomorphisms) is countable; it constitutes a basis

Basis

Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...

of LQG Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

.

One of the key results of loop quantum gravity is quantization

Quantization (physics)

In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...

of areas: the operator of the area

of a two-dimensional surface

should have a discrete spectrum

Spectrum (disambiguation)

A spectrum is a condition or value that is not limited to a specific set of values but can vary infinitely within a continuum.Spectrum may also refer to:-Physical science:* Electromagnetic spectrum...

. Every spin network is an eigenstate of each such operator, and the area eigenvalue equals

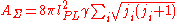
where the sum goes over all intersections

with the spin network. In this formula,

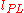is the Planck Length,
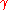is the Immirzi parameter
Immirzi parameter
The Immirzi parameter is a numerical coefficient appearing in loop quantum gravity, a nonperturbative theory of quantum gravity. The Immirzi parameter measures the size of the quantum of area in Planck units...

and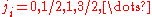
is the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...

associated with the link of the spin network. The two-dimensional area is therefore "concentrated" in the intersections with the spin network.

According to this formula, the lowest possible non-zero eigenvalue of the area operator corresponds to a link that carries spin 1/2 representation. Assuming an Immirzi parameter

Immirzi parameter

The Immirzi parameter is a numerical coefficient appearing in loop quantum gravity, a nonperturbative theory of quantum gravity. The Immirzi parameter measures the size of the quantum of area in Planck units...

on the order of 1, this gives the smallest possible measurable area of ~10⁻⁶⁶ cm².

The formula for area eigenvalues becomes somewhat more complicated if the surface is allowed to pass through the nodes (it is not yet clear if these situations are physically meaningful.)

Similar quantization applies to the volume operator. The volume of 3-d submanifold that contains part of spin network is given by a sum of contributions from each node inside it. One can think that every node in a spin network is an elementary "quantum of volume" and every link is a "quantum of area" surrounding this volume.

More general gauge theories

Similar constructions can be made for general gauge theories with a compact Lie group G and a connection form

Connection form

In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....

. This is actually an exact duality

Duality (mathematics)

In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...

over a lattice. Over a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

however, assumptions like diffeomorphism invariance are needed to make the duality exact (smearing Wilson loop

Wilson loop

In gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...

s is tricky). Later, it was generalized by Robert Oeckl to representations of quantum group

Quantum group

In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...

s in 2 and 3 dimensions using the Tannaka-Krein duality

Tannaka-Krein duality

In mathematics, Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. Its natural extension to the non-Abelian case is the Grothendieck duality theory....

.

Michael A. Levin and Xiao-Gang Wen have also defined string-nets using tensor categories that are objects very similar to spin networks. However the exact connection with spin networks is not clear yet. String-net condensation produces topologically ordered

Topological order

In physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...

states in condensed matter.

Usage in mathematics