Penrose graphical notation
Encyclopedia
In mathematics
and physics
, Penrose graphical notation or tensor diagram notation is a (usually handwritten) visual depiction of multilinear functions or tensor
s proposed by Roger Penrose
. A diagram in the notation consists of several shapes linked together by lines, much like tinker toys. The notation has been studied extensively by Predrag Cvitanović
, who used it to classify the classical Lie groups
. It has also been generalized using representation theory
to spin networks in physics, and with the presence of matrix group
s to trace diagram
s in linear algebra.
, each shape represents a multilinear function. The lines attached to shapes represent the inputs or outputs of a function, and attaching shapes together in some way is essentially the composition of functions.
, a particular tensor is associated with a particular shape with many lines projecting upwards and downwards, corresponding to abstract
upper and lower indices of tensors respectively. Connecting lines between two shapes corresponds to contraction of indices
. One advantage of this notation
is that one does not have to invent new letters for new indices. This notation is also explicitly basis
-independent
is done horizontally, and matrix multiplication
is done vertically.
is represented by a U-shaped loop or an upside-down U-shaped loop, depending on the type of tensor that is used.
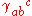) of a Lie algebra
are represented by a small triangle with one line pointing upwards and two lines pointing downwards.
of indices is conveniently represented by joining the index lines together.
(
) is represented by a circle around the tensor(s) to be differentiated and a line joined from the circle pointing downwards to represent the lower index of the derivative.
" of tensor manipulations.
For example,
, where n is the number of dimensions, is a common "identity".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Penrose graphical notation or tensor diagram notation is a (usually handwritten) visual depiction of multilinear functions or tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s proposed by Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
. A diagram in the notation consists of several shapes linked together by lines, much like tinker toys. The notation has been studied extensively by Predrag Cvitanović
Predrag Cvitanovic
Predrag Cvitanović, is currently an endowed Professor of Physics at the Georgia Institute of Technology. He is highly regarded for his work in nonlinear dynamics, particularly his contributions to periodic orbit theory...
, who used it to classify the classical Lie groups
. It has also been generalized using representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
to spin networks in physics, and with the presence of matrix group
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
s to trace diagram
Trace diagram
In mathematics, trace diagrams are a graphical means of performing computations in linear and multilinear algebra. They can be represented as graphs in which some edges are labeled by matrices. The simplest trace diagrams represent the trace and determinant of a matrix...
s in linear algebra.
Multilinear algebra
In the language of multilinear algebraMultilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
, each shape represents a multilinear function. The lines attached to shapes represent the inputs or outputs of a function, and attaching shapes together in some way is essentially the composition of functions.
Tensors
In the language of tensor algebraTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, a particular tensor is associated with a particular shape with many lines projecting upwards and downwards, corresponding to abstract
Abstract index notation
Abstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any fixed basis and, in particular, are non-numerical...
upper and lower indices of tensors respectively. Connecting lines between two shapes corresponds to contraction of indices
Tensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
. One advantage of this notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
is that one does not have to invent new letters for new indices. This notation is also explicitly basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
-independent
Matrices
Each shape represents a matrix, and tensor multiplicationTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
is done horizontally, and matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
is done vertically.
Metric tensor
The metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is represented by a U-shaped loop or an upside-down U-shaped loop, depending on the type of tensor that is used.
 |
 |
Levi-Civita tensor
The Levi-Civita antisymmetric tensor is represented by a thick horizontal bar with sticks pointing downwards or upwards, depending on the type of tensor that is used. |
 |
 |
Structure constant
The structure constants (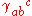) of a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
are represented by a small triangle with one line pointing upwards and two lines pointing downwards.
 |
Contraction of indices
ContractionTensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
of indices is conveniently represented by joining the index lines together.
Symmetrization
Symmetrization of indices is represented by a thick zig-zag or wavy bar crossing the index lines horizontally. |
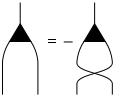
Antisymmetrization
Antisymmetrization of indices is represented by a thick straight line crossing the index lines horizontally. |
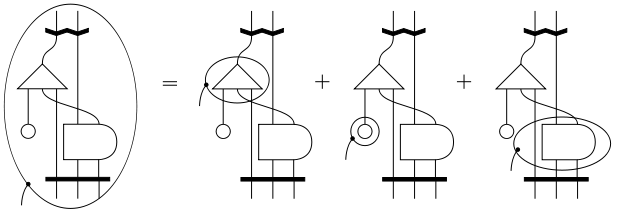
Covariant derivative
The covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
(
) is represented by a circle around the tensor(s) to be differentiated and a line joined from the circle pointing downwards to represent the lower index of the derivative.
 |
Tensor manipulation
The diagrammatic notation is very useful in manipulating tensor algebra. It usually involves a few simple "identitiesIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
" of tensor manipulations.
For example,
, where n is the number of dimensions, is a common "identity".See also
- Braided monoidal category
- Spin networks
- Trace diagramTrace diagramIn mathematics, trace diagrams are a graphical means of performing computations in linear and multilinear algebra. They can be represented as graphs in which some edges are labeled by matrices. The simplest trace diagrams represent the trace and determinant of a matrix...
- Abstract index notationAbstract index notationAbstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any fixed basis and, in particular, are non-numerical...