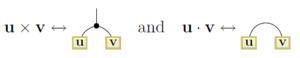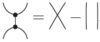In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, trace diagrams are a graphical means of performing computations in linear

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

 and multilinear algebra

Multilinear algebra

In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...

. They can be represented as (slightly modified) graphs

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

 in which some edges are labeled by matrices

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

. The simplest trace diagrams represent the trace

Trace (linear algebra)

In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...

 and determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 of a matrix. Several results in linear algebra, such as Cramer's Rule

Cramer's rule

In linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...

 and the Cayley–Hamilton theorem

Cayley–Hamilton theorem

In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....

, have simple diagrammatic proofs. They are closely related to Penrose's graphical notation.

Formal definition

Let V be a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 of dimension

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 n over a field F (with n≥2), and let Fun(V,V) denote the linear transformations on V. An n-trace diagram is a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

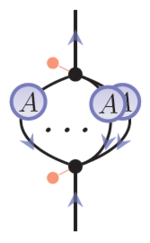
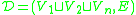 , where the sets V_i (i = 1, 2, n) are composed of vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 of degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

 i, together with the following additional structures:

• a ciliation at each vertex in the graph, which is an explicit ordering of the adjacent edges at that vertex;
• a labeling V₂ → Fun(V,V) associating each degree-2 vertex to a linear transformation.

Note that V₂ and V_n should be considered as distinct sets in the case n = 2. A framed trace diagram is a trace diagram together with a partition of the degree-1 vertices V₁ into two disjoint ordered collections called the inputs and the outputs.

The "graph" underlying a trace diagram may have the following special features, which are not always included in the standard definition of a graph:

• Loops
  Loop (graph theory)
  In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
  
   are permitted (a loop is an edges that connects a vertex to itself).
• Edges that have no vertices are permitted, and are represented by small circles.
• Multiple edges between the same two vertices are permitted.

Drawing conventions

• When trace diagrams are drawn, the ciliation on an n-vertex is commonly represented by a small mark between two of the incident edges (in the figure above, a small red dot); the specific ordering of edges follows by proceeding counter-clockwise from this mark.
• The ciliation and labeling at a degree-2 vertex are combined into a single directed node that allows one to differentiate the first edge (the incoming edge) from the second edge (the outgoing edge).
• Framed diagrams are drawn with inputs at the bottom of the diagram and outputs at the top of the diagram. In both cases, the ordering corresponds to reading from left to right.

Correspondence with multilinear functions

Every framed trace diagram corresponds to a multilinear function between tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

 powers of the vector space V. The degree-1 vertices correspond to the inputs and outputs of the function, while the degree-n vertices correspond to the generalized Levi-Civita symbol

Levi-Civita symbol

The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...

 (which is an anti-symmetric tensor related to the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

). If a diagram has no output strands, its function maps tensor products to a scalar. If there are no degree-1 vertices, the diagram is said to be closed and its corresponding function may be identified with a scalar.

By definition, a trace diagram's function is computed using signed graph coloring. For each edge coloring

Edge coloring

In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...

 of the graph's edges by n labels, so that no two edges adjacent to the same vertex have the same label, one assigns a weight based on the labels at the vertices and the labels adjacent to the matrix labels. These weights become the coefficients of the diagram's function.

In practice, a trace diagram's function is typically computed by decomposing the diagram into smaller pieces whose functions are known. The overall function can then be computed by re-composing the individual functions.

3-Vector diagrams

Several vector identities have easy proofs using trace diagrams. This section covers 3-trace diagrams. In the translation of diagrams to functions, it can be shown that the positions of ciliations at the degree-3 vertices has no influence on the resulting function, so they may be omitted.

It can be shown that the cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

 and dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

 of 3-dimensional vectors are represented by

In this picture, the inputs to the function are shown as vectors in yellow boxes at the bottom of the diagram. The cross product diagram has an output vector, represented by the free strand at the top of the diagram. The dot product diagram does not have an output vector; hence, its output is a scalar.

As a first example, consider the scalar triple product identity


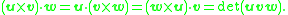
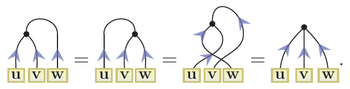
To prove this diagrammatically, note that all of the following figures are different depictions of the same 3-trace diagram (as specified by the above definition):

Combining the above diagrams for the cross product and the dot product, one can read off the three leftmost diagrams as precisely the three leftmost scalar triple products in the above identity. It can also be shown that the rightmost diagram represents det[u v w]. The scalar triple product identity follows because each is a different representation of the same diagram's function.

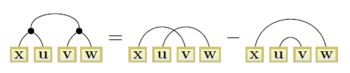
As a second example, one can show that

(where the equality indicates that the identity holds for the underlying multilinear functions). One can show that this kind of identity does not change by "bending" the diagram or attaching more diagrams, provided the changes are consistent across all diagrams in the identity. Thus, one can bend the top of the diagram down to the bottom, and attach vectors to each of the free edges, to obtain

which reads
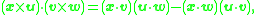
a well-known identity relating four 3-dimensional vectors.

Diagrams with matrices

The simplest closed diagrams with a single matrix label correspond to the coefficients of the characteristic polynomial

Characteristic polynomial

In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

, up to a scalar factor that depends only on the dimension of the matrix. One representation of these diagrams is shown below, where is used to indicate equality up to a scalar factor that depends only on the dimension n of the underlying vector space.

.

Properties

Let G be the group of n×n matrices. If a closed trace diagram is labeled by k different matrices, it may be interpreted as a function from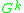 to an algebra of multilinear functions. This function is invariant

Invariant (mathematics)

In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...

 under simultaneous conjugation

Conjugacy class

In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...

, that is, the function corresponding to is the same as the function corresponding to for any invertible .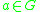

Extensions and applications

Trace diagrams may be specialized for particular Lie groups by altering the definition slightly. In this context, they are sometimes called birdtracks, tensor diagrams

Penrose graphical notation

In mathematics and physics, Penrose graphical notation or tensor diagram notation is a visual depiction of multilinear functions or tensors proposed by Roger Penrose. A diagram in the notation consists of several shapes linked together by lines, much like tinker toys...

, or Penrose graphical notation

Penrose graphical notation

In mathematics and physics, Penrose graphical notation or tensor diagram notation is a visual depiction of multilinear functions or tensors proposed by Roger Penrose. A diagram in the notation consists of several shapes linked together by lines, much like tinker toys...

.

Trace diagrams have primarily been used by physicists as a tool for studying Lie groups. The most common applications use representation theory

Representation theory

Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...

 to construct spin networks from trace diagrams. In mathematics, they have been used to study character varieties.