
Small cancellation theory
Encyclopedia
In the mathematical subject of group theory
, small cancellation theory studies groups given by group presentations
satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. It turns out that small cancellation conditions have substantial implications for algebraic, geometric and algorithmic properties of the group. Finitely presented groups satisfying sufficiently strong small cancellation conditions are word hyperbolic and have word problem
solvable by Dehn's algorithm. Small cancellation methods are also used for constructing Tarski monsters
, and for solutions of Burnside's problem
.
in 1910s. Dehn proved that fundamental groups of closed orientable surfaces of genus at least two have word problem
solvable by what is now called Dehn's algorithm. His proof involved drawing the Cayley graph
of such a group in the hyperbolic plane
and performing curvature estimates via the Gauss-Bonnet theorem for a closed loop in the Cayley graph to conclude that such a loop must contain a large portion (more than a half) of a defining relation.
A 1949 paper of Tartakovskii was an immediate precursor for small cancellation theory: this paper provided a solution of the word problem for a class of groups satisfying a complicated set of combinatorial conditions, where small cancellation type assumptions played a key role. The standard version of small cancellation theory, as it is used today, was developed by Martin Greendlinger in a series of papers in early 1960s, who primarily dealt with the "metric" small cancellation conditions. In particular, Greendlinger proved that finitely presented groups satisfying the C'(1/6) small cancellation condition have word problem solvable by Dehn's algorithm. The theory was further refined and formalized in the subsequent work of Lyndon, Schupp and Lyndon-Schupp, who also treated the case of non-metric small cancellation conditions and developed a version of small cancellation theory for amalgamated free products and HNN-extensions.
Small cancellation theory was further generalized by Alexander Ol'shanskii who developed a "graded" version of the theory where the set of defining relations comes equipped with a filtration and where a defining relator of a particular grade is allowed to have a large overlap with a defining relator of a higher grade. Olshaskii used graded small cancellation theory to construct various "monster" groups, including the Tarski monster
and also to give a new proof that free Burnside groups
of large odd exponent are infinite (this result was originally proved by Adian
and Novikov in 1968 using more combinatorial methods).
Small cancellation theory supplied a basic set of examples and ideas for the theory of word-hyperbolic groups that was put forward by Gromov in a seminal 1987 monograph "Hyperbolic groups".
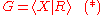
be a group presentation
where R ⊆ F(X) is a set of freely reduced and cyclically reduced words in the free group
F(X) such that R is symmetrized, that is, closed under taking cyclic permutations and inverses.
A nontrivial freely reduced word u in F(X) is called a piece with respect to (∗) if there exist two distinct elements r1, r2 in R that both have u as maximal initial segment.
Note that if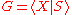 is a group presentation where the set of defining relators S is not symmetrized, we can always take the symmetrized closure R of S, where R consists of all cyclic permutations of elements of S and S−1. Then R is symmetrized and
is a group presentation where the set of defining relators S is not symmetrized, we can always take the symmetrized closure R of S, where R consists of all cyclic permutations of elements of S and S−1. Then R is symmetrized and 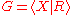 is also a presentation of G.
is also a presentation of G.
The condition C'(λ) is sometimes called a metric small cancellation condition.

where ui are pieces and where the above product is freely reduced as written, then m ≥ p. That is, no defining relator can be written as a reduced product of fewer than p pieces.
Let q ≥ 3 be an integer. A group presentation (∗) as above is said to satisfy the T(q) small cancellation condition if whenever 3 ≤ t < q and r1,...,rt in R are such that r1 ≠ r2−1,...,
rt ≠ r1−1 then at least one of the products r1r2,...,rt−1rt, rtr1 is freely reduced as written.
Geometrically, condition T(q) essentially means that if D is a reduced van Kampen diagram
over (∗) then every interior vertex of D of degree at least three actually has degree at least q.
Greendlinger's lemma:
Let (∗) be a group presentation as above satisfying the C'(λ) small cancellation condition where 0 ≤ λ ≤ 1/6. Let w ∈ F(X) be a nontrivial freely reduced word such that w = 1 in G. Then there is a subword v of w and a defining relator r ∈ R such that v is also a subword of r and such that
Note that the assumption λ ≤ 1/6 implies that (1-3λ) ≥ 1/2, so that w contains a subword more than a half of some defining relator.
Greendlinger's lemma is obtained as a corollary of the following geometric statement:
Under the assumptions of Greendlinger's lemma, let D be a reduced van Kampen diagram
over (∗) with a cyclically reduced boundary label such that D contains at least two regions. Then there exist two distinct regions D1 and D2 in D such that for j = 1,2 the region Dj intersects the boundary cycle ∂D of D in a simple arc whose length is bigger than (1-3λ)|∂Dj|.
This result in turn is proved by considering a dual diagram for D. There one defines a combinatorial notion of curvature (which, by the small cancellation assumptions, is negative at every interior vertex), and one then obtains a combinatorial version of the Gauss-Bonnet theorem. Greendlinger's lemma is proved as a consequence of this analysis and in this way the proof evokes the ideas of the original proof of Dehn for the case of surface groups.
Note that we always have
which implies that the process must terminate in at most |w| steps. Moreover all the words wj represent the same element of G as does w and hence if the process terminates with the empty word, then w represents the identity element of G.
One says that for a symmetrized presentation (∗) Dehn's algorithm solves the word problem
in G if the converse is also true, that is if for any freely reduced word w in F(X) this word represents the identity element of G if and only if Dehn's algorithm, starting from w, terminates in the empty word.
Greendlinger's lemma implies that for a C'(1/6) presentation Dehn's algorithm solves the word problem.
If a C'(1/6) presentation (∗) is finite (that is both X and R are finite), then Dehn's algorithm is an actual non-deterministic
algorithm
in the sense of recursion theory
. However, even if (∗) is an infinite C'(1/6) presentation, Dehn's algorithm, understood as an abstract procedure, still correctly decides whether or not a word in the generators X±1 represents the identity element of G.
in the following sense. Consider a minimal subset S of R such that the symmetrized closure of S is equal to R. Thus if r and s are distinct elements of S then r is not a cyclic permutation of s±1 and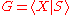 is another presentation for G. Let Y be the presentation complex
is another presentation for G. Let Y be the presentation complex
for this presentation. Then (see and Theorem 13.3 in ), under the above assumptions on (∗), Y is a classifying space
for G, that is G = π1(Y) and the universal cover of Y is contractible
. In particular, this implies that G is torsion-free and has cohomological dimension
two.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, small cancellation theory studies groups given by group presentations
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. It turns out that small cancellation conditions have substantial implications for algebraic, geometric and algorithmic properties of the group. Finitely presented groups satisfying sufficiently strong small cancellation conditions are word hyperbolic and have word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
solvable by Dehn's algorithm. Small cancellation methods are also used for constructing Tarski monsters
Tarski monster group
In mathematics, a Tarski monster group, named for Alfred Tarski, is an infinite group G, such that every proper subgroup H of G, other than the identity subgroup, is a cyclic group of order a fixed prime number p. A Tarski monster group is necessarily simple. It was shown by A. Yu...
, and for solutions of Burnside's problem
Burnside's problem
The Burnside problem, posed by William Burnside in 1902 and one of the oldest and most influential questions in group theory, asks whether a finitely generated group in which every element has finite order must necessarily be a finite group...
.
History
Some ideas underlying the small cancellation theory go back to the work of Max DehnMax Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
in 1910s. Dehn proved that fundamental groups of closed orientable surfaces of genus at least two have word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
solvable by what is now called Dehn's algorithm. His proof involved drawing the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of such a group in the hyperbolic plane
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
and performing curvature estimates via the Gauss-Bonnet theorem for a closed loop in the Cayley graph to conclude that such a loop must contain a large portion (more than a half) of a defining relation.
A 1949 paper of Tartakovskii was an immediate precursor for small cancellation theory: this paper provided a solution of the word problem for a class of groups satisfying a complicated set of combinatorial conditions, where small cancellation type assumptions played a key role. The standard version of small cancellation theory, as it is used today, was developed by Martin Greendlinger in a series of papers in early 1960s, who primarily dealt with the "metric" small cancellation conditions. In particular, Greendlinger proved that finitely presented groups satisfying the C'(1/6) small cancellation condition have word problem solvable by Dehn's algorithm. The theory was further refined and formalized in the subsequent work of Lyndon, Schupp and Lyndon-Schupp, who also treated the case of non-metric small cancellation conditions and developed a version of small cancellation theory for amalgamated free products and HNN-extensions.
Small cancellation theory was further generalized by Alexander Ol'shanskii who developed a "graded" version of the theory where the set of defining relations comes equipped with a filtration and where a defining relator of a particular grade is allowed to have a large overlap with a defining relator of a higher grade. Olshaskii used graded small cancellation theory to construct various "monster" groups, including the Tarski monster
Tarski monster group
In mathematics, a Tarski monster group, named for Alfred Tarski, is an infinite group G, such that every proper subgroup H of G, other than the identity subgroup, is a cyclic group of order a fixed prime number p. A Tarski monster group is necessarily simple. It was shown by A. Yu...
and also to give a new proof that free Burnside groups
Burnside's problem
The Burnside problem, posed by William Burnside in 1902 and one of the oldest and most influential questions in group theory, asks whether a finitely generated group in which every element has finite order must necessarily be a finite group...
of large odd exponent are infinite (this result was originally proved by Adian
Sergei Adian
Sergei Ivanovich Adian, also Adjan is one of the most prominent Soviet and Russian mathematicians. He is a professor at the Moscow State University. He is most famous for his work in group theory, especially on the Burnside problem.-Biography:...
and Novikov in 1968 using more combinatorial methods).
Small cancellation theory supplied a basic set of examples and ideas for the theory of word-hyperbolic groups that was put forward by Gromov in a seminal 1987 monograph "Hyperbolic groups".
Pieces
Let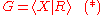
be a group presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
where R ⊆ F(X) is a set of freely reduced and cyclically reduced words in the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
F(X) such that R is symmetrized, that is, closed under taking cyclic permutations and inverses.
A nontrivial freely reduced word u in F(X) is called a piece with respect to (∗) if there exist two distinct elements r1, r2 in R that both have u as maximal initial segment.
Note that if
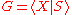 is a group presentation where the set of defining relators S is not symmetrized, we can always take the symmetrized closure R of S, where R consists of all cyclic permutations of elements of S and S−1. Then R is symmetrized and
is a group presentation where the set of defining relators S is not symmetrized, we can always take the symmetrized closure R of S, where R consists of all cyclic permutations of elements of S and S−1. Then R is symmetrized and 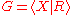 is also a presentation of G.
is also a presentation of G.Metric small cancellation conditions
Let 0 < λ < 1. Presentation (∗) as above is said to satisfy the C'(λ) small cancellation condition if whenever u is a piece with respect to (∗) and u is a subword of some r ∈ R, then |u| < λ|r|. Here |v| is the length of a word v.The condition C'(λ) is sometimes called a metric small cancellation condition.
Non-metric small cancellation conditions
Let p ≥ 3 be an integer. A group presentation (∗) as above is said to satisfy the C(p) small cancellation condition if whenever r ∈ R and
where ui are pieces and where the above product is freely reduced as written, then m ≥ p. That is, no defining relator can be written as a reduced product of fewer than p pieces.
Let q ≥ 3 be an integer. A group presentation (∗) as above is said to satisfy the T(q) small cancellation condition if whenever 3 ≤ t < q and r1,...,rt in R are such that r1 ≠ r2−1,...,
rt ≠ r1−1 then at least one of the products r1r2,...,rt−1rt, rtr1 is freely reduced as written.
Geometrically, condition T(q) essentially means that if D is a reduced van Kampen diagram
Van Kampen diagram
In the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
over (∗) then every interior vertex of D of degree at least three actually has degree at least q.
Examples
- Let
 be the standard presentation of the free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
be the standard presentation of the free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
of rank two. Then for the symmetrized closure of this presentation the only pieces are words of length 1. This symmetrized form satisfies the C(4)-T(4) small cancellation conditions and the C'(λ) condition for any 1 > λ > 1/4. - Let
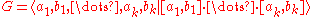 , where k ≥ 2, be the standard presentation of the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, where k ≥ 2, be the standard presentation of the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a closed orientable surface of genus k. Then for the symmetrization of this presentation the only pieces are words of length 1 and this symmetrization satisfies the C'(1/7) and C(8) small cancellation conditions. - Let
 . Then, up to inversion, every piece for the symmetrized version of this presentation, has the form biabj or bi, where 0 ≤ i,j ≤ 100. This symmetrization satisfies the C'(1/20) small cancellation condition.
. Then, up to inversion, every piece for the symmetrized version of this presentation, has the form biabj or bi, where 0 ≤ i,j ≤ 100. This symmetrization satisfies the C'(1/20) small cancellation condition. - If a symmetrized presentation satisfies the C'(1/m) condition then it also satisfies the C(m) condition.
- Let r ∈ F(X) be a nontrivial cyclically reduced word which is not a proper power in F(X) and let n ≥ 2. Then the symmetrized closure of the presentation
 satisfies the C(2n) and C'(1/n) small cancellation conditions.
satisfies the C(2n) and C'(1/n) small cancellation conditions.
Greendlinger's lemma
The main result regarding the metric small cancellation condition is the following statement (see Theorem 4.4 in Ch. V of) which is usually calledGreendlinger's lemma:
Let (∗) be a group presentation as above satisfying the C'(λ) small cancellation condition where 0 ≤ λ ≤ 1/6. Let w ∈ F(X) be a nontrivial freely reduced word such that w = 1 in G. Then there is a subword v of w and a defining relator r ∈ R such that v is also a subword of r and such that
- |v| > (1 − 3λ)|r|.
Note that the assumption λ ≤ 1/6 implies that (1-3λ) ≥ 1/2, so that w contains a subword more than a half of some defining relator.
Greendlinger's lemma is obtained as a corollary of the following geometric statement:
Under the assumptions of Greendlinger's lemma, let D be a reduced van Kampen diagram
Van Kampen diagram
In the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
over (∗) with a cyclically reduced boundary label such that D contains at least two regions. Then there exist two distinct regions D1 and D2 in D such that for j = 1,2 the region Dj intersects the boundary cycle ∂D of D in a simple arc whose length is bigger than (1-3λ)|∂Dj|.
This result in turn is proved by considering a dual diagram for D. There one defines a combinatorial notion of curvature (which, by the small cancellation assumptions, is negative at every interior vertex), and one then obtains a combinatorial version of the Gauss-Bonnet theorem. Greendlinger's lemma is proved as a consequence of this analysis and in this way the proof evokes the ideas of the original proof of Dehn for the case of surface groups.
Dehn's algorithm
For any symmetrized group presentation (∗), the following abstract procedure is called Dehn's algorithm:- Given a freely reduced word w on X±1, construct a sequence of freely reduced words w = w0, w1, w2,..., as follows.
- Suppose wj is already constructed. If it is the empty word, terminate the algorithm. Otherwise check if wj contains a subword v such that v is also a subword of some defining relator r = vu ∈ R such that |v| > |r|/2. If no, terminate the algorithm with output wj. If yes, replace v by u−1 in wj, then freely reduce, denote the resulting freely reduced word by wj+1and go to the next step of the algorithm.
Note that we always have
- |w0| > |w1| > |w2| >...
which implies that the process must terminate in at most |w| steps. Moreover all the words wj represent the same element of G as does w and hence if the process terminates with the empty word, then w represents the identity element of G.
One says that for a symmetrized presentation (∗) Dehn's algorithm solves the word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
in G if the converse is also true, that is if for any freely reduced word w in F(X) this word represents the identity element of G if and only if Dehn's algorithm, starting from w, terminates in the empty word.
Greendlinger's lemma implies that for a C'(1/6) presentation Dehn's algorithm solves the word problem.
If a C'(1/6) presentation (∗) is finite (that is both X and R are finite), then Dehn's algorithm is an actual non-deterministic
Nondeterministic algorithm
In computer science, a nondeterministic algorithm is an algorithm that can exhibit different behaviors on different runs, as opposed to a deterministic algorithm. There are several ways an algorithm may behave differently from run to run. A concurrent algorithm can perform differently on different...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
in the sense of recursion theory
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
. However, even if (∗) is an infinite C'(1/6) presentation, Dehn's algorithm, understood as an abstract procedure, still correctly decides whether or not a word in the generators X±1 represents the identity element of G.
Asphericity
Let (∗) be a C'(1/6) or, more generally, C(6) presentation where every r ∈ R is not a proper power in F(X) then G is asphericalAspherical space
In topology, a branch of mathematics, an aspherical space is a topological space with all higher homotopy groups equal to 0.If one works with CW complexes, one can reformulate this condition: an aspherical CW complex is a CW complex whose universal cover is contractible. Indeed, contractibility of...
in the following sense. Consider a minimal subset S of R such that the symmetrized closure of S is equal to R. Thus if r and s are distinct elements of S then r is not a cyclic permutation of s±1 and
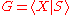 is another presentation for G. Let Y be the presentation complex
is another presentation for G. Let Y be the presentation complexPresentation complex
In geometric group theory, a presentation complex is a 2-dimensional cell complex associated to any presentation of a group G. The complex has a single vertex, and one loop at the vertex for each generator of G...
for this presentation. Then (see and Theorem 13.3 in ), under the above assumptions on (∗), Y is a classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for G, that is G = π1(Y) and the universal cover of Y is contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
. In particular, this implies that G is torsion-free and has cohomological dimension
Cohomological dimension
In abstract algebra, cohomological dimension is an invariant which measures the homological complexity of representations of a group. It has important applications in geometric group theory, topology, and algebraic number theory....
two.
More general curvature
More generally, it is possible to define various sorts of local "curvature" on any van Kampen diagram to be - very roughly - the average excess of vertices + faces - edges (which, by Euler's formula, must total 2) and, by showing, in a particular group, that this is always non-positive (or - even better - negative) internally, show that the curvature must all be on or near the boundary and thereby try to obtain a solution of the word problem. Furthermore one can restrict attention to diagrams that do not contain any of a set of "regions" such that there is a "smaller" region with the same boundary.Other basic properties of small cancellation groups
- Let (∗) be a C'(1/6) presentation. Then an element g in G has order n > 1 if and only if there is a relator r in R of the form r = sn in F(X) such that g is conjugateConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to s in G. In particular, if all elements of R are not proper powers in F(X) then G is torsion-free. - If (∗) is a finite C'(1/6) presentation, the group G is word-hyperbolic.
- If R and S are finite symmetrized subsets of F(X) with equal normal closureNormal closureThe term normal closure is used in two senses in mathematics:* In group theory, the normal closure of a subset of a group is the smallest normal subgroup that contains the subset; see conjugate closure....
s in F(X) such that both presentations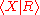 and
and 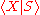 satisfy the C'(1/6) condition then R = S.
satisfy the C'(1/6) condition then R = S. - If a finite presentation (∗) satisfies one of C'(1/6), C'(1/4)–T(4), C(6), C(4)–T(4), C(3)–T(6) then the group G has solvable word problemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
and solvable conjugacy problemConjugacy problemIn abstract algebra, the conjugacy problem for a group G with a given presentation is the decision problem of determining, given two words x and y in G, whether or not they represent conjugate elements of G...
Applications
Examples of applications of small cancellation theory include:- Solution of the conjugacy problemConjugacy problemIn abstract algebra, the conjugacy problem for a group G with a given presentation is the decision problem of determining, given two words x and y in G, whether or not they represent conjugate elements of G...
for groups of alternating knotAlternating knotIn knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
s (see and Chapter V, Theorem 8.5 in ), via showing that for such knots augmented knot groups admit C(T)–T(4) presentations. - Finitely presented C'(1/6) small cancellation groups are basic examples of word-hyperbolic groups. One of the equivalent characterizations of word-hyperbolic groups is as those admitting finite presentations where Dehn's algorithm solves the word problemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
. - Finitely presented groups given by finite C(4)–T(4) presentations where every piece has length one are basic examples of CAT(0) groups: for such a presentation the universal cover of the presentation complexPresentation complexIn geometric group theory, a presentation complex is a 2-dimensional cell complex associated to any presentation of a group G. The complex has a single vertex, and one loop at the vertex for each generator of G...
is a CAT(0)CAT(k) spaceIn mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
square complex. - Early applications of small cancellation theory involve obtaining various embeddability results. Examples include a 1974 paper of Sacerdote and Schupp with a proof that every one-relator group with at least three generators is SQ-universalSQ universal groupIn mathematics, in the realm of group theory, a countable group is said to be SQ-universal if every countable group can be embedded in one of its quotient groups...
and a 1976 paper of Schupp with a proof that every countable group can be embedded into a simple groupSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
generated by an element of order two and an element of order three. - The so-called Rips construction, due to Eliyahu RipsEliyahu RipsEliyahu Rips, also Ilya Rips is a Latvian-born Israeli mathematician known for his research in geometric group theory. He became known to the general public following his coauthoring a paper on the Torah Code....
, provides a rich source of counter-examples regarding various subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
properties of word-hyperbolic groups: Given an arbitrary finitely presented group Q, the construction produces a short exact sequence where K is two-generated and where G is torsion-free and given by a finite C'(1/6)-presentation (and thus G is word-hyperbolic). The construction yields proofs of unsolvability of several algorithmic problems for word-hyperbolic groups, including the subgroup membership problem, the generation problem and the rank problem. Also, with a few exceptions, the group K in the Rips construction is not finitely presentable. This implies that there exist word-hyperbolic groups that are not coherent that is which contain subgroups that are finitely generated but not finitely presentable.
where K is two-generated and where G is torsion-free and given by a finite C'(1/6)-presentation (and thus G is word-hyperbolic). The construction yields proofs of unsolvability of several algorithmic problems for word-hyperbolic groups, including the subgroup membership problem, the generation problem and the rank problem. Also, with a few exceptions, the group K in the Rips construction is not finitely presentable. This implies that there exist word-hyperbolic groups that are not coherent that is which contain subgroups that are finitely generated but not finitely presentable. - Small cancellation methods (for infinite presentations) were used by Ol'shanskii to construct various "monster" groups, including the Tarski monsterTarski monster groupIn mathematics, a Tarski monster group, named for Alfred Tarski, is an infinite group G, such that every proper subgroup H of G, other than the identity subgroup, is a cyclic group of order a fixed prime number p. A Tarski monster group is necessarily simple. It was shown by A. Yu...
and also to give a proof that free Burnside groups of large odd exponent are infinite (a similar result was originally proved by Adian and Novikov in 1968 using more combinatorial methods). Some other "monster" groups constructed by Ol'shanskii using this methods include: an infinite simpleSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
Noetherian group; an infinite group in which every proper subgroup has prime order and any two subgroups of the same order are conjugate; a nonamenable groupAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
where every proper subgroup is cyclic; and others. - BowditchBrian BowditchBrian Hayward Bowditch is a British mathematician known for his contributions to geometry and topology, particularly in the areas of geometric group theory and low-dimensional topology. He is also known for solving the angel problem...
used infinite small cancellation presentations to prove that there exist continuumly many quasi-isometry typesQuasi-isometryIn mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
of two-generator groups. - Thomas and Velickovic used small cancellation theory to construct a finitely generated group with two non-homeomorphic asymptotic cones, thus answering a question of Gromov.
- McCammond and Wise showed how to overcome difficulties posed by the Rips construction and produce large classes of small cancellation groups that are coherent (that is where all finitely generated subgroups are finitely presented) and, moreover, locally quasiconvex (that is where all finitely generated subgroups are quasiconvex).
- Small cancellation methods play a key role in the study of various models of "generic" or "random" finitely presented groupsRandom groupIn mathematics, random groups are certain groups obtained by a probabilistic construction. They were introduced by Misha Gromov to answer questions such as "What does a typical group look like?"...
(see ). In particular, for a fixed number m ≥ 2 of generators and a fixed number t ≥ 1 of defining relations and for any λ < 1 a random m-generator t-relator group satisfies the C'(λ) small cancellation condition. Even if the number of defining relations t is not fixed but grows as (2m−1)εn (where ε ≥ 0 is the fixed density parameter in Gromov's density model of "random" groups, and where is the length of the defining relations), then an ε-random group satisfies the C'(1/6) condition provided ε < 1/12.
is the length of the defining relations), then an ε-random group satisfies the C'(1/6) condition provided ε < 1/12. - Gromov used a version of small cancellation theory with respect to a graph to prove the existence of a finitely presented group that "contains" (in the appropriate sense) an infinite sequence of expandersExpander graphIn combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below...
and therefore does not admit a uniform embedding into a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. This result provides a direction (the only one available so far) for looking for counter-examples to the Novikov conjectureNovikov conjectureThe Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965....
. - Osin used a generalization of small cancellation theory to obtain an analog of Thurston's hyperbolic Dehn surgery theoremHyperbolic Dehn surgeryIn mathematics, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifolds from a given cusped hyperbolic 3-manifold...
for relatively hyperbolic groupRelatively hyperbolic groupIn mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group...
s.
Generalizations
- A version of small cancellation theory for quotient groups of amalgamated free productsFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
and HNN extensionHNN extensionIn mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s was developed in the paper of Sacerdote and Schupp and then in the book of Lyndon and Schupp. - Ol'shanskii developed a "stratified" version of small cancellation theory where the set of relators is filtered as an ascending union of stata (each stratum satisfying a small cancellation condition) and for a relator r from some statum and a relator s from a higher stratum their overlap is required to be small with respect to |s| but is allowed to have a large with respect to |r|. This theory allowed Ol'shanskii to construct various "moster" groups including the Tarski monsterTarski monster groupIn mathematics, a Tarski monster group, named for Alfred Tarski, is an infinite group G, such that every proper subgroup H of G, other than the identity subgroup, is a cyclic group of order a fixed prime number p. A Tarski monster group is necessarily simple. It was shown by A. Yu...
and to give a new proof that free Burnside groups of large odd exponent are infinite. - Ol'shanskii and Delzant later on developed versions of small cancellation theory for quotients of word-hyperbolic groups.
- McCammond provided a higher-dimensional version of small cancellation theory.
- McCammond and Wise pushed substantially further the basic results of the standard small cancellation theory (such as Greendlinger's lemma) regarding the geometry of van Kampen diagramVan Kampen diagramIn the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
s over small cancellation presentations. - Gromov used a version of small cancellation theory with respect to a graph to prove the existence of a finitely presented group that "contains" (in the appropriate sense) an infinite sequence of expanders and therefore does not admit a uniform embedding into a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. See also for more details on small cancellation theory with respect to a graph. - Osin gave a version of small cancellation theory for quotiens of relatively hyperbolic groupRelatively hyperbolic groupIn mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group...
s and used it to obtain a relatively hyperbolic generalization of Thurston's hyperbolic Dehn surgery theoremHyperbolic Dehn surgeryIn mathematics, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifolds from a given cusped hyperbolic 3-manifold...
.
Basic references
- Roger Lyndon and Paul Schupp, Combinatorial group theory. Reprint of the 1977 edition. Classics in Mathematics. Springer-Verlag, Berlin, 2001. ISBN: 3-540-41158-5.
- Alexander Yu. Olʹshanskii, Geometry of defining relations in groups. Translated from the 1989 Russian original by Yu. A. Bakhturin. Mathematics and its Applications (Soviet Series), 70. Kluwer Academic Publishers Group, Dordrecht, 1991. ISBN: 0-7923-1394-1.
- Ralph Strebel, Appendix. Small cancellation groups. Sur les groupes hyperboliques d'après Mikhael Gromov (Bern, 1988), pp. 227–273, Progress in Mathematics, 83, Birkhäuser Boston, Boston, MA, 1990. ISBN: 0-8176-3508-4.
- Milé Krajčevski, Tilings of the plane, hyperbolic groups and small cancellation conditions. Memoirs of the American Mathematical Society, vol. 154 (2001), no. 733.
See also
- Geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
- Word-hyperbolic group
- Tarski monster groupTarski monster groupIn mathematics, a Tarski monster group, named for Alfred Tarski, is an infinite group G, such that every proper subgroup H of G, other than the identity subgroup, is a cyclic group of order a fixed prime number p. A Tarski monster group is necessarily simple. It was shown by A. Yu...
- Burnside problem
- Finitely presented group
- Word problem for groupsWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
- Van Kampen diagramVan Kampen diagramIn the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...

