
Rank of a group
Encyclopedia
In the mathematical
subject of group theory
, the rank of a group G, denoted rank(G), can refer to the smallest cardinality of a generating
set for G, that is

If G is a finitely generated group, then the rank of G is a nonnegative integer. The notion of rank of a group is a group-theoretic analog of the notion of dimension of a vector space. Indeed, for p-groups
, the rank of the group P is the dimension of the vector space P/Φ(P), where Φ(P) is the Frattini subgroup
.
The rank of a group is also often defined in such a way as to ensure subgroups have rank less than or equal to the whole group, which is automatically the case for dimensions of vector spaces, but not for groups such as affine group
s. To distinguish these different definitions, one sometimes calls this rank the subgroup rank. Explicitly, the subgroup rank of a group G is the maximum of the ranks of its subgroups:
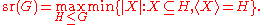
Sometimes the subgroup rank is restricted to abelian subgroups.
, known as the rank problem. The problem asks, for a particular class of finitely presented groups if there exists an algorithm that, given a finite presentation of a group from the class, computes the rank of that group. The rank problem is one of the harder algorithmic problems studied in group theory and relatively little is known about it. Known results include:
F(X) → G, where F(X) is the free group
with free basis X. There is a dual notion of co-rank of a finitely generated group G defined as the largest cardinality of X such that there exists an onto homomorphism
G → F(X). Unlike rank, co-rank is always algorithmically computable for finitely presented groups, using the algorithm of Makanin and Razborov
for solving systems of equations in free groups.
The notion of co-rank is related to the notion of a cut number for 3-manifolds.
If p is a prime number
, then the p-rank of G is the largest rank of an elementary abelian
p-subgroup. The sectional p-rank is the largest rank of an elementary abelian p-section (quotient of a subgroup).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subject of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the rank of a group G, denoted rank(G), can refer to the smallest cardinality of a generating
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
set for G, that is

If G is a finitely generated group, then the rank of G is a nonnegative integer. The notion of rank of a group is a group-theoretic analog of the notion of dimension of a vector space. Indeed, for p-groups
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
, the rank of the group P is the dimension of the vector space P/Φ(P), where Φ(P) is the Frattini subgroup
Frattini subgroup
In mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
.
The rank of a group is also often defined in such a way as to ensure subgroups have rank less than or equal to the whole group, which is automatically the case for dimensions of vector spaces, but not for groups such as affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
s. To distinguish these different definitions, one sometimes calls this rank the subgroup rank. Explicitly, the subgroup rank of a group G is the maximum of the ranks of its subgroups:
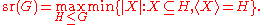
Sometimes the subgroup rank is restricted to abelian subgroups.
Known facts and examples
- For a nontrivial group G, we have rank(G)=1 if and only if G is a cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. - For a free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
 we have
we have 
- If X is a set and G = F(X) is the free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with free basis X then rank(G) = |X|. - If a group H is a homomorphic imageGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
(or a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
) of a group G then rank(H) ≤ rank(G). - If G is a finite non-abelian simple groupSimple groupIn mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
(e.g. G = An, the alternating group, for n > 4) then rank(G) = 2. This fact is a consequence of the Classification of finite simple groupsClassification of finite simple groupsIn mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
. - If G is a finitely generated group and Φ(G) ≤ G is the Frattini subgroupFrattini subgroupIn mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
of G (which is always normal in G so that the quotient group G/Φ(G) is defined) then rank(G) = rank(G/Φ(G)). - If G is the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a closed (that is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and without boundary) connected 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
M then rank(G)≤g(M), where g(M) is the Heegaard genus of M. - If H,K ≤ F(X) are finitely generated subgroups of a free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
F(X) such that the intersection is nontrivial, then L is finitely generated and
is nontrivial, then L is finitely generated and
- rank(L) − 1 ≤ 2(rank(K) − 1)(rank(H) − 1).
- This result is due to Hanna NeumannHanna NeumannJohanna Neumann was a German-born mathematician who worked on group theory.Johanna was born in Lankwitz, Steglitz-Zehlendorf, Germany. She attended Auguste-Viktoria-Schule and the University of Berlin and completed her studies in 1936 with distinctions in mathematics and physics. She began...
. A famous conjecture called the Hanna Neumann conjectureHanna Neumann conjectureIn the mathematical subject of group theory, the Hanna Neumann conjecture is a statement about the rank of the intersection of two finitely generated subgroups of a free group. The conjecture was posed by Hanna Neumann in 1957...
states that in fact one always has rank(L) − 1 ≤ (rank(K) − 1)(rank(H) − 1). Despite a great deal of effort invested in attacking this problem (see, for example), the Hanna Neumann Conjecture remains open.- According to the classic Grushko theoremGrushko theoremIn the mathematical subject of group theory, the Grushko theorem or the Grushko-Neumann theorem is a theorem stating that the rank of a free product of two groups is equal to the sum of the ranks of the two free factors...
, rank behaves additively with respect to taking free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
s, that is, for any groups A and B we have
- According to the classic Grushko theorem
- rank(A
 B) = rank(A) + rank(B).
B) = rank(A) + rank(B).
- If
 is a one-relator group such that r is not a primitive elementPrimitive elementIn mathematics, the term primitive element can mean:* Primitive root modulo n, in number theory* Primitive element , an element that generates a given field extension...
is a one-relator group such that r is not a primitive elementPrimitive elementIn mathematics, the term primitive element can mean:* Primitive root modulo n, in number theory* Primitive element , an element that generates a given field extension...
in the free group F(x1,..., xn), that is, r does not belong to a free basis of F(x1,..., xn), then rank(G) = n.
- If
The rank problem
There is an algorithmic problem studied in group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, known as the rank problem. The problem asks, for a particular class of finitely presented groups if there exists an algorithm that, given a finite presentation of a group from the class, computes the rank of that group. The rank problem is one of the harder algorithmic problems studied in group theory and relatively little is known about it. Known results include:
- The rank problem is algorithmically undecidable for the class of all finitely presented groups. Indeed, by a classical result of Adian-Rabin, there is no algorithm to decide if a finitely presented group is trivial, so even the question of whether rank(G)=0 is undecidable for finitely presented groups.
- The rank problem is decidable for finite groups and for finitely generated abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s. - The rank problem is decidable for finitely generated nilpotent groupNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
s. The reason is that for such a group G, the Frattini subgroupFrattini subgroupIn mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
of G contains the commutator subgroupCommutator subgroupIn mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of G and hence the rank of G is equal to the rank of the abelianization of G. - The rank problem is undecidable for word hyperbolic groups.
- The rank problem is decidable for torsion-free Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s. - The rank problem is open for finitely generated virtually abelian groups (that is containing an abelian subgroup of finite indexIndex of a subgroupIn mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
), for virtually free groups, and for 3-manifold3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
groups.
Generalizations and related notions
The rank of a finitely generated group G can be equivalently defined as the smallest cardinality of a set X such that there exists an onto homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
F(X) → G, where F(X) is the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with free basis X. There is a dual notion of co-rank of a finitely generated group G defined as the largest cardinality of X such that there exists an onto homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
G → F(X). Unlike rank, co-rank is always algorithmically computable for finitely presented groups, using the algorithm of Makanin and Razborov
Alexander Razborov
Aleksandr Aleksandrovich Razborov , sometimes known as Sasha Razborov, is a Soviet and Russian mathematician and computational theorist who won the Nevanlinna Prize in 1990 for introducing the "approximation method" in proving Boolean circuit lower bounds of some essential algorithmic problems, and...
for solving systems of equations in free groups.
The notion of co-rank is related to the notion of a cut number for 3-manifolds.
If p is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, then the p-rank of G is the largest rank of an elementary abelian
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
p-subgroup. The sectional p-rank is the largest rank of an elementary abelian p-section (quotient of a subgroup).
See also
- Generating set of a groupGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
- Grushko theoremGrushko theoremIn the mathematical subject of group theory, the Grushko theorem or the Grushko-Neumann theorem is a theorem stating that the rank of a free product of two groups is equal to the sum of the ranks of the two free factors...
- Free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
- Nielsen equivalence

