
SQ universal group
Encyclopedia
In mathematics
, in the realm of group theory
, a countable group
is said to be SQ-universal if every countable group can be embedded in one of its quotient
groups. SQ-universality can be thought of as a measure of largeness or complexity of a group.
, Bernhard Neumann
and Hanna Neumann
proved that every countable group can be embedded in a two-generator group. Using the contemporary language of SQ-universality, this result says that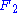 , the free group
, the free group
(non-abelian
) on two generators
, is SQ-universal. This is the first known example of an SQ-universal group. Many more examples are now known:
In addition much stronger versions of the Higmann-Neumann-Neumann theorem are now known. Ould Houcine has proved:
 , say, must be embeddable in a quotient of an SQ-universal group
, say, must be embeddable in a quotient of an SQ-universal group 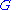 . If
. If 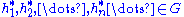 are chosen such that
are chosen such that  for all
for all 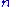 , then they must freely generate a free subgroup of
, then they must freely generate a free subgroup of 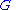 . Hence:
. Hence:
Since every countable group can be embedded in a countable simple group
, it is often sufficient to consider embeddings of simple groups. This observation allows us to easily prove some elementary results about SQ-universal groups, for instance:
To prove this suppose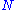 is not SQ-universal, then there is a countable group
is not SQ-universal, then there is a countable group  that cannot be embedded into a quotient group of
that cannot be embedded into a quotient group of 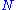 . Let
. Let  be any countable group, then the direct product
be any countable group, then the direct product
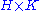 is also countable and hence can be embedded in a countable simple group
is also countable and hence can be embedded in a countable simple group 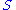 . Now, by hypotheseis,
. Now, by hypotheseis,  is SQ-universal so
is SQ-universal so 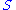 can be embedded in a quotient group,
can be embedded in a quotient group, 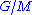 , say, of
, say, of  . The second isomorphism theorem
. The second isomorphism theorem
tells us:
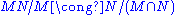
Now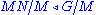 and
and 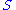 is a simple subgroup of
is a simple subgroup of 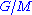 so either:
so either:
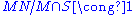
or:
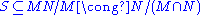 .
.
The latter cannot be true because it implies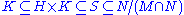 contrary to our choice of
contrary to our choice of  . It follows that
. It follows that 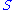 can be embedded in
can be embedded in 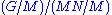 , which by the third isomorphism theorem
, which by the third isomorphism theorem
is isomorphic to , which is in turn isomorphic to
, which is in turn isomorphic to 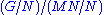 . Thus
. Thus  has been embedded into a quotient group of
has been embedded into a quotient group of  , and since
, and since 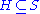 was an arbitrary countable group, it follows that
was an arbitrary countable group, it follows that 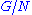 is SQ-universal.
is SQ-universal.
Since every subgroup
 of finite index in a group
of finite index in a group  contains a normal subgroup
contains a normal subgroup 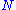 also of finite index in
also of finite index in  , it easily follows that:
, it easily follows that:
Let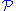 be a class of groups. (For the purposes of this section, groups are defined up to isomorphism
be a class of groups. (For the purposes of this section, groups are defined up to isomorphism
) A group is called SQ-universal in the class
is called SQ-universal in the class 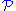 if
if 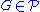 and every countable group in
and every countable group in 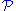 is isomorphic to a subgroup of a quotient of
is isomorphic to a subgroup of a quotient of  . The following result can be proved:
. The following result can be proved:
Let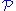 be a class of groups. A group
be a class of groups. A group  is called SQ-universal for the class
is called SQ-universal for the class 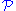 if every group in
if every group in  is isomorphic to a subgroup of a quotient of
is isomorphic to a subgroup of a quotient of  . Note that there is no requirement that
. Note that there is no requirement that 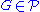 nor that any groups be countable.
nor that any groups be countable.
The standard definition of SQ-universality is equivalent to SQ-universality both in and for the class of countable groups.
Given a countable group , call an SQ-universal group
, call an SQ-universal group 
 -stable, if every non-trivial factor group of
-stable, if every non-trivial factor group of  contains a copy of
contains a copy of  . Let
. Let 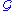 be the class of finitely presented SQ-universal groups that are
be the class of finitely presented SQ-universal groups that are  -stable for some
-stable for some  then Houcine's version of the HNN theorem that can be re-stated as:
then Houcine's version of the HNN theorem that can be re-stated as:
However there are uncountably many finitely generated groups, and a countable group can only have countably many finitely generated subgroups. It is easy to see from this that:
An infinite class of groups is wrappable if given any groups
of groups is wrappable if given any groups 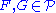 there exists a simple group
there exists a simple group 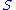 and a group
and a group 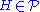 such that
such that 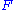 and
and  can be embedded in
can be embedded in 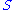 and
and 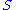 can be embedded in
can be embedded in  . The it is easy to prove:
. The it is easy to prove:
The motivation for the definition of wrappable class comes from results such as the Boone-Higman theorem, which states that a countable group has soluble word problem if and only if it can be embedded in a simple group
has soluble word problem if and only if it can be embedded in a simple group 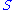 that can be embedded in a finitely presented group
that can be embedded in a finitely presented group 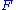 . Houcine has shown that the group
. Houcine has shown that the group  can be constructed so that it too has soluble word problem. This together with the fact that taking the direct product of two groups preserves solubility of the word problem shows that:
can be constructed so that it too has soluble word problem. This together with the fact that taking the direct product of two groups preserves solubility of the word problem shows that:
Other examples of wrappable classes of groups are:
The fact that a class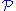 is wrappable does not imply that any groups are SQ-universal for
is wrappable does not imply that any groups are SQ-universal for
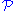 . It is clear, for instance, that some sort of cardinality restriction for the members of
. It is clear, for instance, that some sort of cardinality restriction for the members of 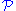 is required.
is required.
If we replace the phrase "isomorphic to a subgroup of a quotient of" with "isomorphic to a subgroup of" in the definition of "SQ-universal", we obtain the stronger concept of S-universal (respectively S-universal for/in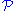 ). The Higman Embedding Theorem can be used to prove that there is a finitely presented group that contains a copy of every finitely presented group. If
). The Higman Embedding Theorem can be used to prove that there is a finitely presented group that contains a copy of every finitely presented group. If 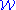 is the class of all finitely presented groups with soluble word problem, then it is known that there is no uniform algorithm
is the class of all finitely presented groups with soluble word problem, then it is known that there is no uniform algorithm
to solve the word problem for groups in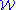 . It follows, although the proof is not a straightforward as one might expect, that no group in
. It follows, although the proof is not a straightforward as one might expect, that no group in 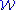 can contain a copy of every group in
can contain a copy of every group in 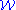 . But it is clear that any SQ-universal group is a fortiori SQ-universal for
. But it is clear that any SQ-universal group is a fortiori SQ-universal for 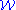 . If we let
. If we let 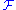 be the class of finitely presented groups, and
be the class of finitely presented groups, and  be the free group on two generators, we can sum this up as:
be the free group on two generators, we can sum this up as:
The following questions are open (the second implies the first):
While it is quite difficult to prove that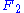 is SQ-universal, the fact that it is SQ-universal for the class of finite groups follows easily from these two facts:
is SQ-universal, the fact that it is SQ-universal for the class of finite groups follows easily from these two facts:
 is a category and
is a category and 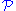 is a class of objects of
is a class of objects of  , then the definition of SQ-universal for
, then the definition of SQ-universal for 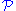 clearly makes sense. If
clearly makes sense. If  is a concrete category
is a concrete category
, then the definition of SQ-universal in also makes sense. As in the group theoretic case, we use the term SQ-universal for an object that is SQ-universal both for and in the class of countable objects of
also makes sense. As in the group theoretic case, we use the term SQ-universal for an object that is SQ-universal both for and in the class of countable objects of  .
.
Many embedding theorems can be restated in terms of SQ-universality. Shirshov's Theorem that a Lie algebra
of finite or countable dimension can be embedded into a 2-generator Lie algebra is equivalent to the statement that the 2-generator free Lie algebra is SQ-universal (in the category of Lie algebras). This can be proved by proving a version of the Higman, Neumann, Neumann theorem for Lie algebras. However versions of the HNN theorem can be proved for categories where there is no clear idea of a free object. For instance it can be proved that every separable topological group
is isomorphic to a topological subgroup of a group having two topological generators (that is, having a dense
2-generator subgroup).
A similar concept holds for free lattice
s. The free lattice in three generators is countably infinite. It has, as a sublattice, the free lattice in four generators, and, by induction, as a sublattice, the free lattice in a countable number of generators.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the realm of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a countable group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is said to be SQ-universal if every countable group can be embedded in one of its quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
groups. SQ-universality can be thought of as a measure of largeness or complexity of a group.
History
Many classic results of combinatorial group theory, going back to 1949, are now interpreted as saying that a particular group or class of groups is (are) SQ-universal. However the first explicit use of the term seems to be in an address given by Peter Neumann to The London Algebra Colloquium entitled "SQ-universal groups" on 23 May 1968.Examples of SQ-universal groups
In 1949 Graham HigmanGraham Higman
Graham Higman FRS was a leading British mathematician. He is known for his contributions to group theory....
, Bernhard Neumann
Bernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
and Hanna Neumann
Hanna Neumann
Johanna Neumann was a German-born mathematician who worked on group theory.Johanna was born in Lankwitz, Steglitz-Zehlendorf, Germany. She attended Auguste-Viktoria-Schule and the University of Berlin and completed her studies in 1936 with distinctions in mathematics and physics. She began...
proved that every countable group can be embedded in a two-generator group. Using the contemporary language of SQ-universality, this result says that
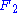 , the free group
, the free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
(non-abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
) on two generators
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
, is SQ-universal. This is the first known example of an SQ-universal group. Many more examples are now known:
- Adding two generators and one arbitrary relator to a nontrivialNontrivialNontrivial is the opposite of trivial. In contexts where trivial has a formal meaning, nontrivial is its antonym.It is a term common among communities of engineers and mathematicians, to indicate a statement or theorem that is not obvious or easy to prove.-Examples:*In mathematics, it is often...
torsion-free group, always results in an SQ-universal group. - Any non-elementary group that is hyperbolicHyperbolicHyperbolic refers to something related to or in shape of hyperbola , or to something employing the literary device of hyperbole .The following topics are based on the hyperbola etymology:...
with respect to a collection of proper subgroups is SQ-universal. - Many HNN extensionHNN extensionIn mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s, free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
s and free products with amalgamation. - The four-generator Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
with presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
: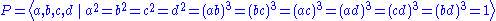
- Charles F. Miller III's example of a finitely presented SQ-universal group all of whose non-trivial quotients have unsolvableUndecidableUndecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
word problemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
.
In addition much stronger versions of the Higmann-Neumann-Neumann theorem are now known. Ould Houcine has proved:
- For every countable group
 there exists a 2-generator SQ-universal group
there exists a 2-generator SQ-universal group  such that
such that  can be embedded in every non-trivial quotient of
can be embedded in every non-trivial quotient of  .
.
Some elementary properties of SQ-universal groups
A free group on countably many generators , say, must be embeddable in a quotient of an SQ-universal group
, say, must be embeddable in a quotient of an SQ-universal group 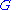 . If
. If 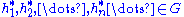 are chosen such that
are chosen such that  for all
for all 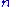 , then they must freely generate a free subgroup of
, then they must freely generate a free subgroup of 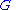 . Hence:
. Hence:- Every SQ-universal group has as a subgroup, a free group on countably many generators.
Since every countable group can be embedded in a countable simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, it is often sufficient to consider embeddings of simple groups. This observation allows us to easily prove some elementary results about SQ-universal groups, for instance:
- If
 is an SQ-universal group and
is an SQ-universal group and 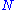 is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of (i.e.
(i.e.  ) then either
) then either 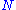 is SQ-universal or the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
is SQ-universal or the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
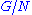 is SQ-universal.
is SQ-universal.
To prove this suppose
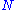 is not SQ-universal, then there is a countable group
is not SQ-universal, then there is a countable group  that cannot be embedded into a quotient group of
that cannot be embedded into a quotient group of 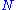 . Let
. Let  be any countable group, then the direct product
be any countable group, then the direct productDirect product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
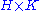 is also countable and hence can be embedded in a countable simple group
is also countable and hence can be embedded in a countable simple group 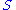 . Now, by hypotheseis,
. Now, by hypotheseis,  is SQ-universal so
is SQ-universal so 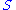 can be embedded in a quotient group,
can be embedded in a quotient group, 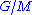 , say, of
, say, of  . The second isomorphism theorem
. The second isomorphism theoremIsomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
tells us:
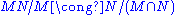
Now
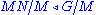 and
and 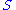 is a simple subgroup of
is a simple subgroup of 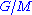 so either:
so either: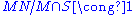
or:
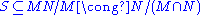 .
.The latter cannot be true because it implies
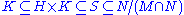 contrary to our choice of
contrary to our choice of  . It follows that
. It follows that 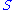 can be embedded in
can be embedded in 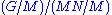 , which by the third isomorphism theorem
, which by the third isomorphism theoremIsomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
is isomorphic to
 , which is in turn isomorphic to
, which is in turn isomorphic to 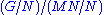 . Thus
. Thus  has been embedded into a quotient group of
has been embedded into a quotient group of  , and since
, and since 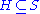 was an arbitrary countable group, it follows that
was an arbitrary countable group, it follows that 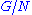 is SQ-universal.
is SQ-universal.Since every subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
 of finite index in a group
of finite index in a group  contains a normal subgroup
contains a normal subgroup 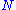 also of finite index in
also of finite index in  , it easily follows that:
, it easily follows that:- If the group
 is of finite index in
is of finite index in  , then
, then  is SQ-universal if and only if
is SQ-universal if and only if  is SQ-universal.
is SQ-universal.
Variants and generalizations of SQ-universality
Several variants of SQ-universality occur in the literature. The reader should be warned that terminology in this area is not yet completely stable and should read this section with this caveat in mind.Let
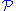 be a class of groups. (For the purposes of this section, groups are defined up to isomorphism
be a class of groups. (For the purposes of this section, groups are defined up to isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
) A group
 is called SQ-universal in the class
is called SQ-universal in the class 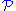 if
if 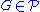 and every countable group in
and every countable group in 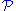 is isomorphic to a subgroup of a quotient of
is isomorphic to a subgroup of a quotient of  . The following result can be proved:
. The following result can be proved:- Let
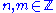 where
where  is odd,
is odd,  and
and 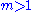 , and let
, and let 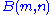 be the free m-generator Burnside group, then every non-cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
be the free m-generator Burnside group, then every non-cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
subgroup of is SQ-universal in the class of groups of exponent
is SQ-universal in the class of groups of exponent  .
.
Let
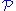 be a class of groups. A group
be a class of groups. A group  is called SQ-universal for the class
is called SQ-universal for the class 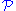 if every group in
if every group in  is isomorphic to a subgroup of a quotient of
is isomorphic to a subgroup of a quotient of  . Note that there is no requirement that
. Note that there is no requirement that 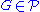 nor that any groups be countable.
nor that any groups be countable.The standard definition of SQ-universality is equivalent to SQ-universality both in and for the class of countable groups.
Given a countable group
 , call an SQ-universal group
, call an SQ-universal group 
 -stable, if every non-trivial factor group of
-stable, if every non-trivial factor group of  contains a copy of
contains a copy of  . Let
. Let 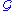 be the class of finitely presented SQ-universal groups that are
be the class of finitely presented SQ-universal groups that are  -stable for some
-stable for some  then Houcine's version of the HNN theorem that can be re-stated as:
then Houcine's version of the HNN theorem that can be re-stated as:- The free group on two generators is SQ-universal for
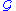 .
.
However there are uncountably many finitely generated groups, and a countable group can only have countably many finitely generated subgroups. It is easy to see from this that:
- No group can be SQ-universal in
 .
.
An infinite class
 of groups is wrappable if given any groups
of groups is wrappable if given any groups 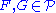 there exists a simple group
there exists a simple group 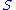 and a group
and a group 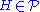 such that
such that 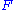 and
and  can be embedded in
can be embedded in 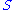 and
and 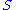 can be embedded in
can be embedded in  . The it is easy to prove:
. The it is easy to prove:- If
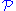 is a wrappable class of groups,
is a wrappable class of groups,  is an SQ-universal for
is an SQ-universal for  and
and 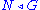 then either
then either 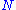 is SQ-universal for
is SQ-universal for 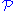 or
or 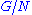 is SQ-universal for
is SQ-universal for 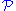 .
.
- If
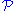 is a wrappable class of groups and
is a wrappable class of groups and  is of finite index in
is of finite index in  then
then  is SQ-universal for the class
is SQ-universal for the class 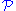 if and only if
if and only if  is SQ-universal for
is SQ-universal for 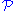 .
.
The motivation for the definition of wrappable class comes from results such as the Boone-Higman theorem, which states that a countable group
 has soluble word problem if and only if it can be embedded in a simple group
has soluble word problem if and only if it can be embedded in a simple group 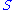 that can be embedded in a finitely presented group
that can be embedded in a finitely presented group 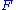 . Houcine has shown that the group
. Houcine has shown that the group  can be constructed so that it too has soluble word problem. This together with the fact that taking the direct product of two groups preserves solubility of the word problem shows that:
can be constructed so that it too has soluble word problem. This together with the fact that taking the direct product of two groups preserves solubility of the word problem shows that:- The class of all finitely presented groups with soluble word problemWord problem (mathematics)In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
is wrappable.
Other examples of wrappable classes of groups are:
- The class of finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s. - The class of torsion free groups.
- The class of countable torsion free groups.
- The class of all groups of a given infinite cardinality.
The fact that a class
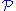 is wrappable does not imply that any groups are SQ-universal for
is wrappable does not imply that any groups are SQ-universal for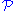 . It is clear, for instance, that some sort of cardinality restriction for the members of
. It is clear, for instance, that some sort of cardinality restriction for the members of 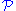 is required.
is required.If we replace the phrase "isomorphic to a subgroup of a quotient of" with "isomorphic to a subgroup of" in the definition of "SQ-universal", we obtain the stronger concept of S-universal (respectively S-universal for/in
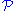 ). The Higman Embedding Theorem can be used to prove that there is a finitely presented group that contains a copy of every finitely presented group. If
). The Higman Embedding Theorem can be used to prove that there is a finitely presented group that contains a copy of every finitely presented group. If 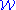 is the class of all finitely presented groups with soluble word problem, then it is known that there is no uniform algorithm
is the class of all finitely presented groups with soluble word problem, then it is known that there is no uniform algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to solve the word problem for groups in
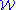 . It follows, although the proof is not a straightforward as one might expect, that no group in
. It follows, although the proof is not a straightforward as one might expect, that no group in 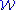 can contain a copy of every group in
can contain a copy of every group in 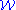 . But it is clear that any SQ-universal group is a fortiori SQ-universal for
. But it is clear that any SQ-universal group is a fortiori SQ-universal for 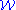 . If we let
. If we let 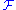 be the class of finitely presented groups, and
be the class of finitely presented groups, and  be the free group on two generators, we can sum this up as:
be the free group on two generators, we can sum this up as: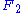 is SQ-universal in
is SQ-universal in 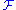 and
and 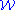 .
.- There exists a group that is S-universal in
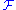 .
. - No group is S-universal in
 .
.
The following questions are open (the second implies the first):
- Is there a countable group that is not SQ-universal but is SQ-universal for
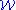 ?
? - Is there a countable group that is not SQ-universal but is SQ-universal in
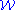 ?
?
While it is quite difficult to prove that
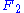 is SQ-universal, the fact that it is SQ-universal for the class of finite groups follows easily from these two facts:
is SQ-universal, the fact that it is SQ-universal for the class of finite groups follows easily from these two facts:- Every symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on a finite set can be generated by two elements - Every finite group can be embedded inside a symmetric group—the natural one being the Cayley group, which is the symmetric group acting on this group as the finite set.
SQ-universality in other categories
If is a category and
is a category and 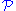 is a class of objects of
is a class of objects of  , then the definition of SQ-universal for
, then the definition of SQ-universal for  clearly makes sense. If
clearly makes sense. If  is a concrete category
is a concrete categoryConcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
, then the definition of SQ-universal in
 also makes sense. As in the group theoretic case, we use the term SQ-universal for an object that is SQ-universal both for and in the class of countable objects of
also makes sense. As in the group theoretic case, we use the term SQ-universal for an object that is SQ-universal both for and in the class of countable objects of  .
.Many embedding theorems can be restated in terms of SQ-universality. Shirshov's Theorem that a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of finite or countable dimension can be embedded into a 2-generator Lie algebra is equivalent to the statement that the 2-generator free Lie algebra is SQ-universal (in the category of Lie algebras). This can be proved by proving a version of the Higman, Neumann, Neumann theorem for Lie algebras. However versions of the HNN theorem can be proved for categories where there is no clear idea of a free object. For instance it can be proved that every separable topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is isomorphic to a topological subgroup of a group having two topological generators (that is, having a dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
2-generator subgroup).
A similar concept holds for free lattice
Free lattice
In mathematics, in the area of order theory, a free lattice is the free object corresponding to a lattice. As free objects, they have the universal property. The word problem for free lattices is also challenging.-Formal definition:...
s. The free lattice in three generators is countably infinite. It has, as a sublattice, the free lattice in four generators, and, by induction, as a sublattice, the free lattice in a countable number of generators.

