
Local coefficients
Encyclopedia
In mathematics
, local coefficients is an idea from algebraic topology
, a kind of half-way stage between homology theory
or cohomology theory with coefficients in the usual sense, in a fixed abelian group
A, and general sheaf cohomology
which, roughly speaking, allows coefficients to vary from point to point in a topological space
X. Such a concept was introduced by Norman Steenrod
.
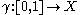 , a morphism
, a morphism 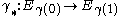 that depends only on the homotopy class with fixed extremities of the path, is the identity on constant paths and such that composition of paths corresponds to compositions of morphisms.
that depends only on the homotopy class with fixed extremities of the path, is the identity on constant paths and such that composition of paths corresponds to compositions of morphisms.
In sheaf theory terms, a constant sheaf
has locally constant function
s as its sections. Consider instead a sheaf F, such that locally on X it is a constant sheaf. That means that in a neighbourhood of any x in X, it is isomorphic to a constant sheaf. Then F may be used as a system of local coefficients on X.
s with flat connections, and from topology by means of linear representations of the fundamental group
.
The cohomology with local coefficients in the module corresponding to the orientation covering can be used to formulate Poincaré duality
for non-orientable manifolds: see Twisted Poincaré duality
.
Larger classes of sheaves are useful: for example the idea of a constructible sheaf
in algebraic geometry
. These turn out, approximately, to be local coefficients away from a singular set.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, local coefficients is an idea from algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a kind of half-way stage between homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
or cohomology theory with coefficients in the usual sense, in a fixed abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
A, and general sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
which, roughly speaking, allows coefficients to vary from point to point in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X. Such a concept was introduced by Norman Steenrod
Norman Steenrod
Norman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
.
Formal definition
Let X be a locally path connected topological space, and M a module over some ring R. A local coefficient system of R-modules E with fiber M is a locally trivial fiber bundle with fiber M with an action of the fundamental groupoid of the base X, that is, for each path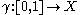 , a morphism
, a morphism 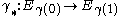 that depends only on the homotopy class with fixed extremities of the path, is the identity on constant paths and such that composition of paths corresponds to compositions of morphisms.
that depends only on the homotopy class with fixed extremities of the path, is the identity on constant paths and such that composition of paths corresponds to compositions of morphisms.In sheaf theory terms, a constant sheaf
Constant sheaf
In mathematics, the constant sheaf on a topological space X associated to a set A is a sheaf of sets on X whose stalks are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset of X the value A, and all of whose restriction maps...
has locally constant function
Locally constant function
In mathematics, a function f from a topological space A to a set B is called locally constant, if for every a in A there exists a neighborhood U of a, such that f is constant on U....
s as its sections. Consider instead a sheaf F, such that locally on X it is a constant sheaf. That means that in a neighbourhood of any x in X, it is isomorphic to a constant sheaf. Then F may be used as a system of local coefficients on X.
Applications
Examples arise geometrically from vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s with flat connections, and from topology by means of linear representations of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
.
The cohomology with local coefficients in the module corresponding to the orientation covering can be used to formulate Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
for non-orientable manifolds: see Twisted Poincaré duality
Twisted Poincaré duality
In mathematics, the twisted Poincaré duality is a theorem removing the restriction on Poincaré duality to oriented manifolds. The existence of a global orientation is replaced by carrying along local information, by means of a local coefficient system....
.
Larger classes of sheaves are useful: for example the idea of a constructible sheaf
Constructible sheaf
In mathematics, a constructible sheaf is a sheaf of abelian groups over some topological space X, such that X is the union of a finite number of locally closed subsets on each of which the sheaf is a twisted constant sheaf...
in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. These turn out, approximately, to be local coefficients away from a singular set.
Links
- A discussion of the notion on Stack exchange

