In algebraic geometry

Algebraic geometry

Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...

, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves

Family of curves

A family of curves is a set of curves, each of which is given by a function or parametrization in which one or more of the parameters is variable. In general, the parameter influence the shape of the curve in a way that is more complicated than a simple linear transformation...

; the dimension of the linear system corresponds to the number of parameters of the family.

These arose first in the form of a linear system of algebraic curve

Algebraic curve

In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...

s in the projective plane

Projective plane

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

. It assumed a more general form, through gradual generalisation, so that one could speak of linear equivalence of divisor

Divisor (algebraic geometry)

In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...

s D on a general algebraic variety

Algebraic variety

In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...

 V.

A linear system of dimension 1, 2, or 3 is called a pencil

Pencil (mathematics)

A pencil in projective geometry is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a projective plane....

, a net, or a web.

Definition by means of functions

Given the fundamental idea of a rational function

Rational function

In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...

 on a general variety V, or in other words of a function f in the function field

Function field of an algebraic variety

In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...

 of V,
divisors D and E are linearly equivalent if


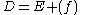
where (f) denotes the divisor of zeroes and poles of the function f.

Note that if V has singular points

Mathematical singularity

In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...

, 'divisor' is inherently ambiguous (Cartier divisors, Weil divisors: see divisor (algebraic geometry)

Divisor (algebraic geometry)

In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...

). The definition in that case is usually said with greater care (using invertible sheaves or holomorphic line bundles); see below.

A complete linear system on V is defined as the set of all effective divisors linearly equivalent to some given divisor D. It is denoted |D|. Let L(D) be the line bundle associated to D. It can be proved that |D| corresponds bijectively to 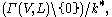and is therefore a projective space.

A linear system 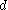is then a projective subspace of a complete linear system, so it corresponds to a vector subspace W of 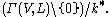The dimension of the linear system is its dimension as a projective space. Hence .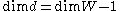

Base locus

If all divisors in the system share a common divisor, this is referred to as the base locus

Base locus

In mathematics, specifically algebraic geometry, the base locus of a linear system of divisors on a variety refers to the subvariety of points 'common' to all divisors in the linear system....

 of the linear system. Geometrically, this corresponds to the common intersection of the varieties. Linear systems may or may not have a base locus – for example, the pencil of affine lines has no common intersection, but given two (nondegenerate) conics in the complex projective plane, they intersect in four points (counting with multiplicity) and thus the pencil they define has these points as base locus.

Linear system of conics

For example, the conic section

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

s in the projective plane form a linear system of dimension five, as one sees by counting the constants in the degree two equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

s. The condition to pass through a given point P imposes a single linear condition, so that conics C through P form a linear system of dimension 4. Other types of condition that are of interest include tangency to a given line L.

In the most elementary treatments a linear system appears in the form of equations


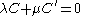
with λ and μ unknown scalars, not both zero. Here C and C′ are given conics. Abstractly we can say that this is a projective line

Projective line

In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...

 in the space of all conics, on which we take


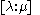
as homogeneous coordinates

Homogeneous coordinates

In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...

. Geometrically we notice that any point Q common to C and C′ is also on each of the conics of the linear system. According to Bézout's theorem

Bézout's theorem

Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...

 C and C′ will intersect in four points (if counted correctly). Assuming these are in general position

General position

In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...

, i.e. four distinct intersections, we get another interpretation of the linear system as the conics passing through the four given points (note that the codimension

Codimension

In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...

 four here matches the dimension, one, in the five-dimensional space of conics). Note that of these conics, exactly three are degenerate

Degenerate conic

In mathematics, a degenerate conic is a conic that fails to be an irreducible curve...

, each consisting of a pair of lines, corresponding to the 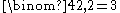ways of choosing 2 pairs of points from 4 points (counting via the multinomial coefficient).

Applications

A striking application of such a family is in which gives a geometric solution to a quartic equation by considering the pencil of conics through the four roots of the quartic, and identifying the three degenerate conics with the three roots of the resolvent cubic.

Example

For example, given the four points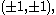 the pencil of conics through them can be parameterized as 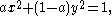which are the affine combinations of the equations 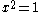and 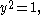corresponding to the parallel vertical lines and horizontal lines; this yields degenerate conics at the standard points of 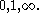A less elegant but more symmetric parametrization is given by 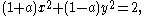in which case inverting a (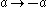) interchanges x and y, yielding the following pencil; in all cases the center is at the origin:

• hyperbolae opening left and right;
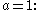• the parallel vertical lines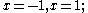
• ellipses with a vertical major axis;
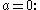• a circle (with radius );
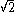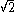• ellipses with a horizontal major axis;
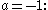• the parallel horizontal lines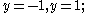
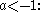• hyperbolae opening up and down,
• the diagonal lines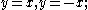
• This then loops around to 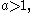since pencils are a projective line.

In the terminology of , this is a Type I linear system of conics, and is animated in the linked video.

Classification

There are 8 types of linear systems of conics over the complex numbers, depending on intersection multiplicity at the base points, which divide into 13 types over the real numbers, depending on whether the base points are real or imaginary; this is discussed in and illustrated in .

Other examples

The Cayley–Bacharach theorem is a property of a pencil of cubics, which states that the base locus satisfies an "8 implies 9" property: any cubic containing 8 of the points necessarily contains the 9th.

Linear systems in birational geometry

In general linear systems became a basic tool of birational geometry

Birational geometry

In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...

 as practised by the Italian school of algebraic geometry

Italian school of algebraic geometry

In relation with the history of mathematics, the Italian school of algebraic geometry refers to the work over half a century or more done internationally in birational geometry, particularly on algebraic surfaces. There were in the region of 30 to 40 leading mathematicians who made major...

. The technical demands became quite stringent; later developments clarified a number of issues. The computation of the relevant dimensions — the Riemann-Roch problem as it can be called — can be better phrased in terms of homological algebra

Homological algebra

Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...

. The effect of working on varieties with singular points

Mathematical singularity

In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...

 is to show up a difference between Weil divisors (in the free abelian group

Free abelian group

In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...

 generated by codimension-one subvarieties), and Cartier divisors coming from sections of invertible sheaves.

The Italian school liked to reduce the geometry on an algebraic surface

Algebraic surface

In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...

 to that of linear systems cut out by surfaces in three-space; Zariski wrote his celebrated book Algebraic Surfaces to try to pull together the methods, involving linear systems with fixed base points. There was a controversy, one of the final issues in the conflict between 'old' and 'new' points of view in algebraic geometry, over Henri Poincaré

Henri Poincaré

Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...

's characteristic linear system of an algebraic family of curves on an algebraic surface.

Line bundle

Line bundle

In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...

/invertible sheaf

Invertible sheaf

In mathematics, an invertible sheaf is a coherent sheaf S on a ringed space X, for which there is an inverse T with respect to tensor product of OX-modules. It is the equivalent in algebraic geometry of the topological notion of a line bundle...

 language

Linear systems are still at the heart of contemporary algebraic geometry; but they are typically introduced by means of the ample line bundle

Ample line bundle

In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...

 language. That is, the language of sheaf theory is considered the most natural starting point, at least to learn the theory. In those terms, divisors D (Cartier divisors, importantly) correspond to line bundles, and linear equivalence of two divisors means that the corresponding line bundles are isomorphic.