Shape optimization
Encyclopedia
Shape optimization is part of the field of optimal control
theory. The typical problem is to find the shape
which is optimal in that it minimizes a certain cost functional
while satisfying given constraints
. In many cases, the functional being solved depends on the solution of a given partial differential equation defined on the variable domain.
Topology optimization
is, in addition, concerned with the number of connected components/boundaries belonging to the domain. Such methods are needed since typically shape optimization methods work in a subset of allowable shapes which have fixed topological properties, such as having a fixed number of holes in them. Topological optimization techniques can then help work around the limitations of pure shape optimization.
, shape optimization can be posed as the problem of finding a bounded set
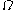, minimizing
a functional
,
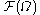possibly subject to a constraint
of the form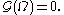
Usually we are interested in sets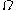
which are Lipschitz
or C1 boundary
and consist of finitely many components, which is a way of saying that we would like to find a rather pleasing shape as a solution, not some jumble of rough bits and pieces. Sometimes additional constraints need to be imposed to that end to ensure well-posedness of the problem and uniqueness of the solution.
Shape optimization is an infinite-dimensional optimization
problem. Furthermore, the space of allowable shapes over which the optimization is performed does not admit a vector space
structure, making application of traditional optimization methods more difficult.
, by using iterative method
s. That is, one starts with an initial guess for a shape, and then gradually evolves it,
until it morphs into the optimal shape.
represent a shape in the computer memory
, and follow its evolution. Several approaches are usually used.
One approach is to follow the boundary of the shape. For that, one can
sample the shape boundary in a relatively dense and uniform manner, that is, to consider enough points to get a sufficiently accurate outline of the shape. Then, one can evolve the shape by gradually moving the boundary points. This is called the Lagrangian approach.
Another approach is to consider a function
defined on a rectangular box around the shape, which is positive inside of the shape, zero on the boundary of the shape, and negative outside of the shape. One can then evolve this function instead of the shape itself. One can consider a rectangular grid on the box and sample the function at the grid points. As the shape evolves, the grid points do not change; only the
function values at the grid points change. This approach, of using a fixed
grid, is called the Eulerian approach. The idea of using a function
to represent the shape is at the basis of the level set method
.
A third approach is to think of the shape evolution as of a flow problem. That is, one can imagine that the shape is made of a plastic material gradually deforming such that any point inside or on the boundary
of the shape can be always traced back to a point of the original shape in a one-to-one fashion. Mathematically, if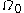
is the initial shape, and 
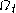is the shape at time t,
one considers the diffeomorphism
s
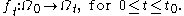
The idea is again that shapes are difficult entities to be dealt with directly, so manipulate them by means of a function.
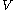and the family of transformations 
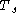of the initial domain 
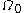under the velocity field 
:
,
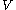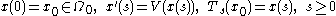and denote
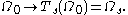
Then the Gateaux or shape derivative of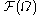
at 
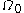with respect to the shape is the limit of
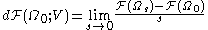
if this limit exists. If in addition the derivative is linear with respect to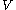
, there is a unique element of 
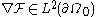and
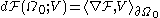
where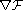
is called the shape gradient. This gives a natural idea of gradient descent
, where the boundary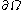
is evolved in the direction of negative shape gradient in order to reduce the value of the cost functional. Higher order derivatives can be similarly defined, leading to Newtonlike methods.
Typically, gradient descent is preferred, even if requires a large number of iterations, because, it can be hard to compute the second-order derivative (that is, the Hessian
) of the objective functional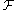
.
If the shape optimization problem has constraints, that is, the functional
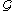is present, one has to find ways to convert the
constrained problem into an unconstrained one. Sometimes ideas based on Lagrange multipliers
can work.
The selection of the parametrization approach depends mainly on the size of the problem: the CAD approach is preferred for small-medium sized models whilst the mesh morphing approach is the best (and sometimes the only feasible one) for large and very large models.
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
theory. The typical problem is to find the shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
which is optimal in that it minimizes a certain cost functional
Functional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
while satisfying given constraints
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
. In many cases, the functional being solved depends on the solution of a given partial differential equation defined on the variable domain.
Topology optimization
Topology optimization
- Introduction :Topology optimisation is a mathematical approach that optimises material layout within a given design space, for a given set of loads and boundary conditions such that the resulting layout meets a prescribed set of performance targets...
is, in addition, concerned with the number of connected components/boundaries belonging to the domain. Such methods are needed since typically shape optimization methods work in a subset of allowable shapes which have fixed topological properties, such as having a fixed number of holes in them. Topological optimization techniques can then help work around the limitations of pure shape optimization.
Definition
MathematicallyMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, shape optimization can be posed as the problem of finding a bounded set
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
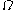, minimizingMaxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
a functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
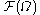,possibly subject to a constraint
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
of the form
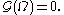
Usually we are interested in sets
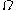which are LipschitzLipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
or C1 boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
and consist of finitely many components, which is a way of saying that we would like to find a rather pleasing shape as a solution, not some jumble of rough bits and pieces. Sometimes additional constraints need to be imposed to that end to ensure well-posedness of the problem and uniqueness of the solution.
Shape optimization is an infinite-dimensional optimization
Infinite-dimensional optimization
In certain optimization problems the unknown optimal solution might not be a number or a vector, but rather a continuous quantity, for example a function or the shape of a body...
problem. Furthermore, the space of allowable shapes over which the optimization is performed does not admit a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
structure, making application of traditional optimization methods more difficult.
Examples
- Among all three-dimensional shapes of given volume, find the one which has minimal surface area. Here:
,
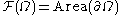with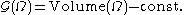
The answer is the inside of a sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
.
- Find the shape of an airplane wing which minimizes dragDrag (physics)In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
. Here the constraints could be
the wing strength, or the wing dimensions.
- Find the shape of various mechanical structures, which can resist a given stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
while having a minimal mass/volume.
- Given a known three-dimensional object with a fixed radiation source inside, deduce the shape and size of the source based on measurements done on part of the boundary of the object. A formulation of this inverse problemInverse problemAn inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
using least-squares fit leads to a shape optimization problem.
Techniques
Shape optimization problems are usually solved numericallyNumerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, by using iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s. That is, one starts with an initial guess for a shape, and then gradually evolves it,
until it morphs into the optimal shape.
Keeping track of the shape
To solve a shape optimization problem, one needs to find a way torepresent a shape in the computer memory
Computer storage
Computer data storage, often called storage or memory, refers to computer components and recording media that retain digital data. Data storage is one of the core functions and fundamental components of computers....
, and follow its evolution. Several approaches are usually used.
One approach is to follow the boundary of the shape. For that, one can
sample the shape boundary in a relatively dense and uniform manner, that is, to consider enough points to get a sufficiently accurate outline of the shape. Then, one can evolve the shape by gradually moving the boundary points. This is called the Lagrangian approach.
Another approach is to consider a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on a rectangular box around the shape, which is positive inside of the shape, zero on the boundary of the shape, and negative outside of the shape. One can then evolve this function instead of the shape itself. One can consider a rectangular grid on the box and sample the function at the grid points. As the shape evolves, the grid points do not change; only the
function values at the grid points change. This approach, of using a fixed
grid, is called the Eulerian approach. The idea of using a function
to represent the shape is at the basis of the level set method
Level set method
The level set method is a numerical technique for tracking interfaces and shapes. The advantage of the level set method is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects...
.
A third approach is to think of the shape evolution as of a flow problem. That is, one can imagine that the shape is made of a plastic material gradually deforming such that any point inside or on the boundary
of the shape can be always traced back to a point of the original shape in a one-to-one fashion. Mathematically, if
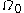is the initial shape, and 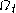is the shape at time t,one considers the diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s
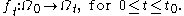
The idea is again that shapes are difficult entities to be dealt with directly, so manipulate them by means of a function.
Iterative methods using shape gradients
Consider a smooth velocity field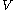 and the family of transformations 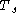of the initial domain 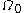under the velocity field 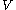: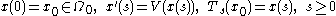,and denote
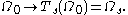
Then the Gateaux or shape derivative of
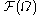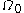at with respect to the shape is the limit of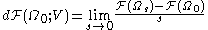if this limit exists. If in addition the derivative is linear with respect to
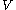, there is a unique element of 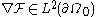and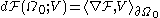where
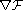is called the shape gradient. This gives a natural idea of gradient descentGradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
, where the boundary
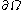is evolved in the direction of negative shape gradient in order to reduce the value of the cost functional. Higher order derivatives can be similarly defined, leading to Newtonlike methods.Typically, gradient descent is preferred, even if requires a large number of iterations, because, it can be hard to compute the second-order derivative (that is, the Hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
) of the objective functional
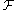.If the shape optimization problem has constraints, that is, the functional
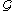is present, one has to find ways to convert theconstrained problem into an unconstrained one. Sometimes ideas based on Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
can work.
Geometry parametrization
Shape optimisation can be faced using standard optimisation methods if a parametrization of the geometry is defined. Such parametrisation is very important in CAE field where goal functions are usually complex functions evaluated using numerical models (CFD, FEA,...). A convenient approach, suitable for a wide class of problems, consists in the parametrisation of the CAD model coupled with a full automation of all the process required for function evaluation (meshing, solving and result processing). Mesh morphing is a valid choice for complex problems. In this case the parametrisation is defined after the meshing stage acting directly on the numerical model used for calculation that is changed using mesh updating methods. There are several algorithms available for mesh morphing (deforming volumes, pseudosolid, Radial Basis Functions).The selection of the parametrization approach depends mainly on the size of the problem: the CAD approach is preferred for small-medium sized models whilst the mesh morphing approach is the best (and sometimes the only feasible one) for large and very large models.
External links
- TopOpt Group — Free interactive programs for 2D and 3D compliance optimization, free MATLAB programme and more information on theory and applications.
- Optopo Group — Simulations and bibliography of the optopo group at Ecole Polytechnique (France). Homogenization method and level set method.