Introduction

Topology optimisation is a mathematical approach that optimises material layout within a given design space, for a given set of loads and boundary conditions such that the resulting layout meets a prescribed set of performance targets. Using topology optimisation, engineers can find the best concept design that meets the design requirements.
Topology optimisation has been implemented through the use of finite element methods for the analysis, and optimisation techniques based on the method of moving asymptotes, genetic algorithms, optimality criteria method, level sets, and topological derivative

Topological derivative

In the fields of shape optimization and topology optimization, a topological derivative is, conceptually, a derivative of a function of a region with respect to infinitesimal changes in its topology, such as adding an infinitesimal hole or crack....

s.

Topology optimisation is used at the concept level of the design process to arrive at a conceptual design proposal that is then fine tuned for performance and manufacturability. This replaces time consuming and costly design iterations and hence reduces design development time and overall cost while improving design performance.

In some cases, proposals from a topology optimisation, although optimal, may be expensive or infeasible to manufacture. These challenges can be overcome through the use of manufacturing constraints in the topology optimisation problem formulation. Using manufacturing constraints, the optimisation yields engineering designs that would satisfy practical manufacturing requirements.
In some cases Additive manufacturing

Additive manufacturing

Additive manufacturing is defined by ASTM as the "process of joining materials to make objects from 3D model data, usually layer upon layer, as opposed to subtractive manufacturing methodologies, such as traditional machining...

 technologies are used to manufacture complex optimized shapes that would otherwise need manufacturing constraints.

Problem Statement

Mathematically one can pose a generic problem as follows:

subject to:

Design Constraints

Governing Differential Equation

The problem statement includes the following

a. Objective functional : This is the goal of the optimization study which is to be minimised over the selection field. For example, one would want to minimise the compliance of a structure to increase structural stiffness.

b. Design space 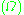: Design space is the allowable volume within which the design can exist. Assembly and packaging requirements, human and tool accessibility are some of the factors that need to be considered in identifying this space . With the definition of the design space, regions or components in the model that cannot be modified during the course of the optimisation are considered as non-design regions.

c. The Discrete Selection Field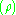: This is the field over which the discrete optimisation is to be performed. It selects or deselects a point on the design space to further the design objective. By selection it has to take the value 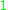and by de-selection it has to take the tvalue .

d. Design constraints: These are design criteria that need to satisfied. These could include material availability constraints, displacement constraints, etc.

e. Governing Differential Equation: This is the one that governs the physics of the structure to be built. For example the elasticity equation in the case of stiff structures would be the governing differential equation.

Implementation Methodology

The optimisation problem posed above implies the need for a discrete optimisation over every point in domain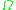 . But, implementation of such a scheme is not yet practicable. So, people adopt continuous optimisation strategies, where they assume that the variable 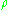varies continuously over the domain 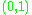. This problem is then solved over a set of finite elements obtained from meshing of the domain.

Topology Optimisation for Stiff Structures

To explain this concept, let us take up the case of the stiff structure optimisation. A stiff structure is one that has the least possible displacement when given certain set of boundary conditions. A global measure of the displacements is the strain energy (also called compliance) of the structure under the prescribed boundary conditions. The lower the strain energy the higher the stiffness of the structure. So, the problem statement involves the objective functional of the strain energy which has to be minimised.

Now the objective functional should be chosen as a function of the selection field 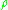. So in literature, people have interpolated the material properties in terms of the selection field. A widely used interpolation scheme is called the Solid Isotropic Material with Penalisation (SIMP). This interpolation is essentially a power law 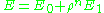that interpolates the Young's modulus of the material to the scalar selection field. 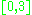The value of varies between in general. This has been shown to confirm to micro-structure of the materials. So one could view topology optimisation to be a process of selection of micro-structure at every point in space so that an objective functional is minimised.

On a broad level, one can visualise that more the material, lesser will be the deflection as there is more material to resist the loads. So, the optimisation requires an opposing constraint, the constraint of the volume. This is in reality a cost factor too and we would not want to spend a lot of money on the material. To obtain the total material utilised an integration of the selection field over the volume can be done.

Finally the elasticity governing differential equations are plugged in so as to get the final problem statement.
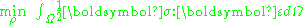
subject to:

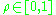
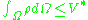
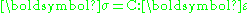
But, a straight forward implementation of such a problem is still infeasible owing to issues such as:

1. Mesh dependency -- Mesh Dependency means that the design obtained on one mesh is not the one that will be obtained on an another mesh. The features of the design become more intricate as the mesh gets refined.
2. Numerical instabilities -- Numerical Instabilities such as checker-board patterns are observed

See Optimisation (mathematics) for a definition of optimisation

Distinction

Topology optimization is distinct from shape optimization

Shape optimization

Shape optimization is part of the field of optimal control theory. The typical problem is to find the shape which is optimal in that it minimizes a certain cost functional while satisfying given constraints...

since typically shape optimisation methods work in a subset of allowable shapes which have fixed topological properties, such as having a fixed number of holes in them. Therefore topology optimisation is used to generate concepts and shape optimisation is used to fine-tune a chosen design topology.

There are various methods used to perform topology optimisation, Solid Isotropic Material with Penalisation (SIMP) and Evolutionary Structural Optimisation (ESO) being two.

External links

• http://www.topopt.dtu.dk - page containing information on the SIMP optimization method.