Level set method
Encyclopedia
The level set method is a numerical
technique for tracking interfaces and shape
s. The advantage of the level set method is that one can perform numerical computations involving curve
s and surfaces on a fixed Cartesian grid without having to parameterize
these objects (this is called the Eulerian approach). Also, the level set method makes it very easy to follow shapes that change topology
, for example when a shape splits in two, develops holes, or the reverse of these operations. All these make the level set method a great tool for modeling time-varying objects, like inflation of an airbag
, or a drop of oil floating in water.
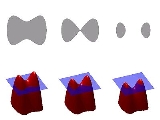
 A very simple, yet powerful way to understand the level set method is by first studying the accompanying illustration before proceeding towards a more technical definition, which then becomes quite accessible. The figure on the right illustrates several important ideas about the level set method. In the upper-left corner we see a shape; that is, a bounded region with a well-behaved boundary. Below it, the red surface is the graph of a level set function
A very simple, yet powerful way to understand the level set method is by first studying the accompanying illustration before proceeding towards a more technical definition, which then becomes quite accessible. The figure on the right illustrates several important ideas about the level set method. In the upper-left corner we see a shape; that is, a bounded region with a well-behaved boundary. Below it, the red surface is the graph of a level set function 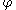 determining this shape, and the flat blue region represents the
determining this shape, and the flat blue region represents the  plane. The boundary of the shape is then the zero level set of
plane. The boundary of the shape is then the zero level set of 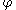 , while the shape itself is the set of points in the plane for which
, while the shape itself is the set of points in the plane for which 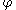 is positive (interior of the shape) or zero (at the boundary).
is positive (interior of the shape) or zero (at the boundary).
In the top row we see the shape changing its topology by splitting in two. It would be quite hard to describe this transformation numerically by parameterizing the boundary of the shape and following its evolution. One would need an algorithm able to detect the moment the shape splits in two, and then construct parameterizations for the two newly obtained curves. On the other hand, if we look at the bottom row, we see that the level set function merely got translated downward. We see that it is much easier to work with a shape through its level set function than with the shape directly, where we would need to watch out for all the possible deformations the shape might undergo.
Thus, in two dimensions, the level set method amounts to representing a closed curve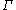 (such as the shape in our example) using an auxiliary function
(such as the shape in our example) using an auxiliary function 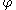 , called the level set function.
, called the level set function. 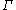 is represented as the zero level set
is represented as the zero level set
of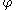 by
by
and the level set method manipulates implicitly, through the function
implicitly, through the function  .
. 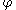 is assumed to take positive values inside the region delimited by the curve
is assumed to take positive values inside the region delimited by the curve 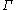 and negative values outside.
and negative values outside.
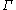 moves in the normal direction with a speed v, then the level set function
moves in the normal direction with a speed v, then the level set function 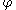 satisfies the level set equation
satisfies the level set equation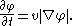
Here, is the Euclidean norm (denoted customarily by single bars in PDEs), and
is the Euclidean norm (denoted customarily by single bars in PDEs), and  is time. This is a partial differential equation
is time. This is a partial differential equation
, in particular a Hamilton-Jacobi equation, and can be solved numerically, for example by using finite difference
s on a Cartesian grid.
The numerical solution of the level set equation, however, requires sophisticated techniques. Simple finite difference methods fail quickly. Upwinding methods, such as the Godunov method
, fare better; however the level set method does not guarantee the conservation of the volume and the shape of the level set in an advection field that does conserve the shape and size, for example uniform or rotational velocity field. Instead, the shape of the level set may get severely distorted and the level set may vanish over several time steps. For this reason, high-order finite difference schemes are generally required, such as high-order essentially non-oscillatory (ENO) schemes, and even then, the feasibility of long-time simulations is questionable. Further sophisticated methods to deal with this difficulty have been developed, e.g., combinations of the level set method with tracing marker particles advected by the velocity field.
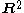 , shrinking in on itself at a constant rate, i.e. each point on the boundary of the circle moves along its inwards pointing normal at some fixed speed. The circle will shrink, and eventually collapse down to a point. If an initial distance field is constructed (i.e. a function whose value is the signed euclidean distance to the boundary (positive interior, negative exterior)) on the initial circle, the normalised gradient of this field will be the circle normal.
, shrinking in on itself at a constant rate, i.e. each point on the boundary of the circle moves along its inwards pointing normal at some fixed speed. The circle will shrink, and eventually collapse down to a point. If an initial distance field is constructed (i.e. a function whose value is the signed euclidean distance to the boundary (positive interior, negative exterior)) on the initial circle, the normalised gradient of this field will be the circle normal.
If the field has a constant value subtracted from it in time, the zero level (which was the initial boundary) of the new fields will also be circular, and will similarly collapse to a point. This is due to this being effectively the temporal integration of the Eikonal equation
with a fixed front velocity.
and James Sethian
. It has become popular in many disciplines, such as image processing
, computer graphics
, computational geometry
, optimization
, and computational fluid dynamics
.
A number of level set data structures have been developed to facilitate the use of the level set method in computer applications.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
technique for tracking interfaces and shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
s. The advantage of the level set method is that one can perform numerical computations involving curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s and surfaces on a fixed Cartesian grid without having to parameterize
Parametric surface
A parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
these objects (this is called the Eulerian approach). Also, the level set method makes it very easy to follow shapes that change topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, for example when a shape splits in two, develops holes, or the reverse of these operations. All these make the level set method a great tool for modeling time-varying objects, like inflation of an airbag
Airbag
An Airbag is a vehicle safety device. It is an occupant restraint consisting of a flexible envelope designed to inflate rapidly during an automobile collision, to prevent occupants from striking interior objects such as the steering wheel or a window...
, or a drop of oil floating in water.
Level set method

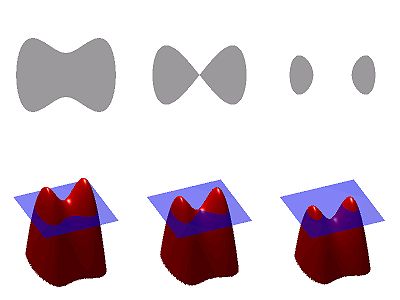
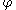 determining this shape, and the flat blue region represents the
determining this shape, and the flat blue region represents the  plane. The boundary of the shape is then the zero level set of
plane. The boundary of the shape is then the zero level set of 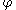 , while the shape itself is the set of points in the plane for which
, while the shape itself is the set of points in the plane for which 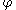 is positive (interior of the shape) or zero (at the boundary).
is positive (interior of the shape) or zero (at the boundary).In the top row we see the shape changing its topology by splitting in two. It would be quite hard to describe this transformation numerically by parameterizing the boundary of the shape and following its evolution. One would need an algorithm able to detect the moment the shape splits in two, and then construct parameterizations for the two newly obtained curves. On the other hand, if we look at the bottom row, we see that the level set function merely got translated downward. We see that it is much easier to work with a shape through its level set function than with the shape directly, where we would need to watch out for all the possible deformations the shape might undergo.
Thus, in two dimensions, the level set method amounts to representing a closed curve
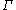 (such as the shape in our example) using an auxiliary function
(such as the shape in our example) using an auxiliary function 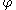 , called the level set function.
, called the level set function. 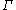 is represented as the zero level set
is represented as the zero level setLevel set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
of
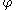 by
by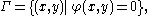
and the level set method manipulates
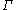 implicitly, through the function
implicitly, through the function 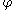 .
. 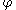 is assumed to take positive values inside the region delimited by the curve
is assumed to take positive values inside the region delimited by the curve 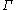 and negative values outside.
and negative values outside.The level set equation
If the curve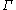 moves in the normal direction with a speed v, then the level set function
moves in the normal direction with a speed v, then the level set function 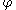 satisfies the level set equation
satisfies the level set equation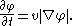
Here,
 is the Euclidean norm (denoted customarily by single bars in PDEs), and
is the Euclidean norm (denoted customarily by single bars in PDEs), and  is time. This is a partial differential equation
is time. This is a partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, in particular a Hamilton-Jacobi equation, and can be solved numerically, for example by using finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
s on a Cartesian grid.
The numerical solution of the level set equation, however, requires sophisticated techniques. Simple finite difference methods fail quickly. Upwinding methods, such as the Godunov method
Godunov's scheme
In numerical analysis and computational fluid dynamics, Godunov's scheme is a conservative numerical scheme, suggested by S. K. Godunov in 1959, for solving partial differential equations...
, fare better; however the level set method does not guarantee the conservation of the volume and the shape of the level set in an advection field that does conserve the shape and size, for example uniform or rotational velocity field. Instead, the shape of the level set may get severely distorted and the level set may vanish over several time steps. For this reason, high-order finite difference schemes are generally required, such as high-order essentially non-oscillatory (ENO) schemes, and even then, the feasibility of long-time simulations is questionable. Further sophisticated methods to deal with this difficulty have been developed, e.g., combinations of the level set method with tracing marker particles advected by the velocity field.
Example
Consider a unit circle in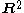 , shrinking in on itself at a constant rate, i.e. each point on the boundary of the circle moves along its inwards pointing normal at some fixed speed. The circle will shrink, and eventually collapse down to a point. If an initial distance field is constructed (i.e. a function whose value is the signed euclidean distance to the boundary (positive interior, negative exterior)) on the initial circle, the normalised gradient of this field will be the circle normal.
, shrinking in on itself at a constant rate, i.e. each point on the boundary of the circle moves along its inwards pointing normal at some fixed speed. The circle will shrink, and eventually collapse down to a point. If an initial distance field is constructed (i.e. a function whose value is the signed euclidean distance to the boundary (positive interior, negative exterior)) on the initial circle, the normalised gradient of this field will be the circle normal.If the field has a constant value subtracted from it in time, the zero level (which was the initial boundary) of the new fields will also be circular, and will similarly collapse to a point. This is due to this being effectively the temporal integration of the Eikonal equation
Eikonal equation
The eikonal equation is a non-linear partial differential equation encountered in problems of wave propagation, when the wave equation is approximated using the WKB theory...
with a fixed front velocity.
History
The level set method was developed in the 1980s by the American mathematicians Stanley OsherStanley Osher
Stanley Osher is an American mathematician, known for his many contributions in shock capturing, level set methods, and PDE-based methods in computer vision and image processing...
and James Sethian
James Sethian
James Albert Sethian is a professor of mathematics at the University of California, Berkeley, and the head of the Mathematics Group at the United States Department of Energy's Lawrence Berkeley National Laboratory....
. It has become popular in many disciplines, such as image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, and computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
.
A number of level set data structures have been developed to facilitate the use of the level set method in computer applications.
See also
- Volume of fluid methodVolume of fluid methodIn computational fluid dynamics, the volume of fluid method is a numerical technique for tracking and locating the free surface . It belongs to the class of Eulerian methods which are characterized by a mesh that is either stationary or is moving in a certain prescribed manner to accommodate the...
- Image segmentation#Level set methods
- Immersed Boundary MethodImmersed boundary methodThe immersed boundary method is an approach – in computational fluid dynamics – to model and simulate mechanical systems in which elastic structures interact with fluid flows...
- LSM/J Level set method for drawing dynamical plane
- LSM/M Level set method for drawing parameter plane
External links
- See Ronald FedkiwRonald FedkiwRonald Paul "Ron" Fedkiw is an associate professor in the Stanford University department of computer science and a leading researcher in the field of computer graphics, focusing on topics relating to physically based simulation of natural phenomena and level sets. His techniques have been...
's academic web page for many stunning pictures and animations showing how the level set method can be used to model real life phenomena, like fire, water, cloth, fracturing materials, etc. - Multivac is a C++ library for front tracking in 2D with level set methods.
- James SethianJames SethianJames Albert Sethian is a professor of mathematics at the University of California, Berkeley, and the head of the Mathematics Group at the United States Department of Energy's Lawrence Berkeley National Laboratory....
's web page on level set method. - Stanley OsherStanley OsherStanley Osher is an American mathematician, known for his many contributions in shock capturing, level set methods, and PDE-based methods in computer vision and image processing...
's homepage.

