
Stalk (sheaf)
Encyclopedia
The stalk of a sheaf
is a mathematical
construction capturing the behaviour of a sheaf around a given point.
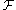 on that small neighborhood should be the same as the behavior of
on that small neighborhood should be the same as the behavior of 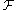 at that point. Of course, no single neighborhood will be small enough, so we will have to take a limit of some sort.
at that point. Of course, no single neighborhood will be small enough, so we will have to take a limit of some sort.
The precise definition is as follows: the stalk of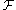 at x, usually denoted
at x, usually denoted  , is:
, is: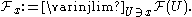
Here the direct limit
is indexed over all the open set
s containing x, with order relation induced by inclusion ( , if
, if 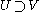 ). By definition (or universal property
). By definition (or universal property
) of the direct limit, an element of the stalk is an equivalence class of elements , where two such sections
, where two such sections  and
and 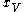 are considered equivalent if the restrictions of the two sections coincide on some neighborhood of x.
are considered equivalent if the restrictions of the two sections coincide on some neighborhood of x.
 is the same as the inverse image
is the same as the inverse image
sheaf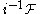 . Notice that the only open sets of the one point space {x} are {x} and ∅, and there is no data over the empty set. Over {x}, however, we get:
. Notice that the only open sets of the one point space {x} are {x} and ∅, and there is no data over the empty set. Over {x}, however, we get: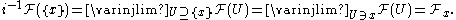
or most categories of algebraic objects such as abelian group
s or rings
.
There is a natural morphism F(U) → Fx for any open set U containing x: it takes a section s in F(U) to its germ, that is, its equivalence class in the direct limit. This is a generalization of the usual concept of a germ
, which can be recovered by looking at the stalks of the sheaf of continuous functions on X.
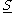 associated to some set or group etc. S has the same set or group as stalks at every point: for any point x, pick an open connected
associated to some set or group etc. S has the same set or group as stalks at every point: for any point x, pick an open connected
neighbourhood. The sections of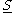 on a connected open equal S and restriction maps are the identities. Therefore the direct limit collapses to yield S as the stalk.
on a connected open equal S and restriction maps are the identities. Therefore the direct limit collapses to yield S as the stalk.
s on an analytic manifold
, a germ of a function at a point determines the function in a small neighborhood of a point. This is because the germ records the function's power series expansion, and all analytic functions are by definition equal to their power series. Using analytic continuation
, we find that the germ at a point determines the function on any connected open set where the function can be everywhere defined. (This does not imply that all the restriction maps of this sheaf are injective!)
s on a smooth manifold, germs contain some local information, but are not enough to reconstruct the function on any open neighborhood. For example, let f : R → R be a bump function which is identically one in a neighborhood of the origin and identically zero far away from the origin. On any sufficiently small neighborhood containing the origin, f is identically one, so at the origin it has the same germ as the constant function with value 1. Suppose that we want to reconstruct f from its germ. Even if we know in advance that f is a bump function, the germ does not tell us how large its bump is. From what the germ tells us, the bump could be infinitely wide, that is, f could equal the constant function with value 1. We cannot even reconstruct f on a small open neighborhood U containing the origin, because we cannot tell whether the bump of f fits entirely in U or whether it is so large that f is identically one in U.
On the other hand, germs of smooth functions can distinguish between the constant function with value one and the function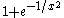 , because the latter function is not identically one on any neighborhood of the origin. This example shows that germs contain more information than the power series expansion of a function, because the power series of
, because the latter function is not identically one on any neighborhood of the origin. This example shows that germs contain more information than the power series expansion of a function, because the power series of 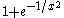 is identically one. (This extra information is related to the fact that the stalk of the sheaf of smooth functions at the origin is a non-Noetherian ring
is identically one. (This extra information is related to the fact that the stalk of the sheaf of smooth functions at the origin is a non-Noetherian ring
. The Krull intersection theorem says that this cannot happen for a Noetherian ring.)
A, the stalk of a quasi-coherent sheaf F corresponding to an A-module M in a point x corresponding to a prime ideal
p is just the localization Mp.
x and a group or ring G has the stalks 0 off x and G in x — whence the name skyscraper
. The same property holds for any point x if the topological space in question is a T1 space
, since every point of a T1 space is closed. This feature is the basis of the construction of Godement resolution
s, used for example in algebraic geometry
to get functor
ial injective resolutions of sheaves.
), it can be expected that the stalks capture a fair amount of the information that the sheaf is encoding. This is indeed true:
In particular:
Both statements are false for presheaves. However, stalks of sheaves and presheaves are tightly linked:
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
is a mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
construction capturing the behaviour of a sheaf around a given point.
Motivation and definition
Sheaves are defined on open sets, but the underlying topological space X consists of points. It is reasonable to attempt to isolate the behavior of a sheaf at a single fixed point x of X. Conceptually speaking, we do this by looking at small neighborhoods of the point. If we look at a sufficiently small neighborhood of x, the behavior of the sheaf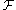 on that small neighborhood should be the same as the behavior of
on that small neighborhood should be the same as the behavior of 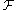 at that point. Of course, no single neighborhood will be small enough, so we will have to take a limit of some sort.
at that point. Of course, no single neighborhood will be small enough, so we will have to take a limit of some sort.The precise definition is as follows: the stalk of
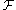 at x, usually denoted
at x, usually denoted  , is:
, is: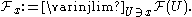
Here the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
is indexed over all the open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s containing x, with order relation induced by inclusion (
 , if
, if 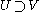 ). By definition (or universal property
). By definition (or universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
) of the direct limit, an element of the stalk is an equivalence class of elements
 , where two such sections
, where two such sections  and
and 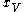 are considered equivalent if the restrictions of the two sections coincide on some neighborhood of x.
are considered equivalent if the restrictions of the two sections coincide on some neighborhood of x.Alternative definition
There is another approach to defining a stalk which is useful in some contexts. Choose a point x of X, and let i be the inclusion of the one point space {x} into X. Then the stalk is the same as the inverse image
is the same as the inverse imageInverse image functor
In mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
sheaf
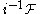 . Notice that the only open sets of the one point space {x} are {x} and ∅, and there is no data over the empty set. Over {x}, however, we get:
. Notice that the only open sets of the one point space {x} are {x} and ∅, and there is no data over the empty set. Over {x}, however, we get: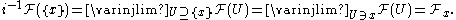
Remarks
For some categories C the direct limit used to define the stalk may not exist. However, it exists for most categories which occur in practice, such as the category of setsCategory of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
or most categories of algebraic objects such as abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
There is a natural morphism F(U) → Fx for any open set U containing x: it takes a section s in F(U) to its germ, that is, its equivalence class in the direct limit. This is a generalization of the usual concept of a germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
, which can be recovered by looking at the stalks of the sheaf of continuous functions on X.
Constant sheaves
The constant sheaf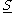 associated to some set or group etc. S has the same set or group as stalks at every point: for any point x, pick an open connected
associated to some set or group etc. S has the same set or group as stalks at every point: for any point x, pick an open connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
neighbourhood. The sections of
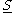 on a connected open equal S and restriction maps are the identities. Therefore the direct limit collapses to yield S as the stalk.
on a connected open equal S and restriction maps are the identities. Therefore the direct limit collapses to yield S as the stalk.Sheaves of analytic functions
For example, in the sheaf of analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s on an analytic manifold
Analytic manifold
In mathematics, an analytic manifold is a topological manifold with analytic transition maps. Every complex manifold is an analytic manifold....
, a germ of a function at a point determines the function in a small neighborhood of a point. This is because the germ records the function's power series expansion, and all analytic functions are by definition equal to their power series. Using analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
, we find that the germ at a point determines the function on any connected open set where the function can be everywhere defined. (This does not imply that all the restriction maps of this sheaf are injective!)
Sheaves of smooth functions
In contrast, for the sheaf of smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s on a smooth manifold, germs contain some local information, but are not enough to reconstruct the function on any open neighborhood. For example, let f : R → R be a bump function which is identically one in a neighborhood of the origin and identically zero far away from the origin. On any sufficiently small neighborhood containing the origin, f is identically one, so at the origin it has the same germ as the constant function with value 1. Suppose that we want to reconstruct f from its germ. Even if we know in advance that f is a bump function, the germ does not tell us how large its bump is. From what the germ tells us, the bump could be infinitely wide, that is, f could equal the constant function with value 1. We cannot even reconstruct f on a small open neighborhood U containing the origin, because we cannot tell whether the bump of f fits entirely in U or whether it is so large that f is identically one in U.
On the other hand, germs of smooth functions can distinguish between the constant function with value one and the function
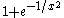 , because the latter function is not identically one on any neighborhood of the origin. This example shows that germs contain more information than the power series expansion of a function, because the power series of
, because the latter function is not identically one on any neighborhood of the origin. This example shows that germs contain more information than the power series expansion of a function, because the power series of 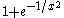 is identically one. (This extra information is related to the fact that the stalk of the sheaf of smooth functions at the origin is a non-Noetherian ring
is identically one. (This extra information is related to the fact that the stalk of the sheaf of smooth functions at the origin is a non-Noetherian ringNoetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
. The Krull intersection theorem says that this cannot happen for a Noetherian ring.)
Quasi-coherent sheaves
On an affine scheme X=SpecSpectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
A, the stalk of a quasi-coherent sheaf F corresponding to an A-module M in a point x corresponding to a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
p is just the localization Mp.
Skyscraper sheaf
On any topological space, the skyscraper sheaf associated to a closed pointClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
x and a group or ring G has the stalks 0 off x and G in x — whence the name skyscraper
Skyscraper
A skyscraper is a tall, continuously habitable building of many stories, often designed for office and commercial use. There is no official definition or height above which a building may be classified as a skyscraper...
. The same property holds for any point x if the topological space in question is a T1 space
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
, since every point of a T1 space is closed. This feature is the basis of the construction of Godement resolution
Godement resolution
The Godement resolution of a sheaf is a construction in homological algebra which allows one to view global, cohomological information about the sheaf in terms of local information coming from its stalks. It is useful for computing sheaf cohomology...
s, used for example in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
to get functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
ial injective resolutions of sheaves.
Properties of the stalk
As outlined in the introduction, stalks capture the local behaviour of a sheaf. As a sheaf is supposed to be determined by its local restrictions (see gluing axiomGluing axiom
In mathematics, the gluing axiom is introduced to define what a sheaf F on a topological space X must satisfy, given that it is a presheaf, which is by definition a contravariant functor...
), it can be expected that the stalks capture a fair amount of the information that the sheaf is encoding. This is indeed true:
- A morphism of sheaves is an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, or monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, respectively, if and only if the induced morphisms on all stalks have the same property. (However it is not true that two sheaves, all of whose stalks are isomorphic, are isomorphic, too, because there may be no map between the sheaves in question).
In particular:
- A sheaf is zero (if we are dealing with sheafs of groups), if and only if all stalks of the sheaf vanish. Therefore the exactnessExact functorIn homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
of a given functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
can be tested on the stalks, which is often easier as one can pass to smaller and smaller neighbourhoods.
Both statements are false for presheaves. However, stalks of sheaves and presheaves are tightly linked:
- Given a presheaf P and its sheafification F, the stalks of P and F agree.

