
Laplace-Beltrami operator
Encyclopedia
In differential geometry, the Laplace operator
, named after Pierre-Simon Laplace
, can be generalized to operate on functions defined on surface
s in Euclidean space
and, more generally, on Riemannian
and pseudo-Riemannian manifold
s. This more general operator goes by the name Laplace–Beltrami operator, after Laplace and Eugenio Beltrami
. Like the Laplacian, the Laplace–Beltrami operator is defined as the divergence
of the gradient
, and is a linear operator taking functions into functions. The operator can be extended to operate on tensors as the divergence of the covariant derivative
. Alternatively, the operator can be generalized to operate on differential forms using the divergence and exterior derivative
. The resulting operator is called the Laplace–de Rham operator (named after Georges de Rham
).

An explicit formula in local coordinates
is possible.
Suppose first that M is an oriented Riemannian manifold
. The orientation allows one to specify a definite volume form
on M, given in an oriented coordinate system xi by
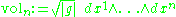
where the dxi are the 1-forms forming the dual basis to the basis vectors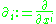
and is the wedge product. Here is the absolute value
is the wedge product. Here is the absolute value
of the determinant
of the metric tensor
gij. The divergence div X of a vector field X on the manifold is then defined as the scalar function with the property
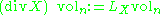
where LX is the Lie derivative
along the vector field
X. In local coordinates, one obtains
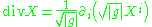
where the Einstein notation
is implied, so that the repeated index i is summed over. The gradient of a scalar function ƒ is the vector field grad f that may be defined through the inner product on the manifold, as
on the manifold, as
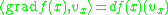
for all vectors vx anchored at point x in the tangent space
TxM of the manifold at point x. Here, dƒ is the exterior derivative
of the function ƒ; it is a 1-form taking argument vx. In local coordinates, one has

where gij are the components of the inverse of the metric tensor, so that with δik the Kronecker delta.
Combining the definitions of the gradient and divergence, the formula for the Laplace–Beltrami operator Δ applied to a scalar function ƒ is, in local coordinates
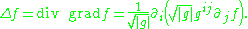
If M is not oriented, then the above calculation carries through exactly as presented, except that the volume form must instead be replaced by a volume element
(a density
rather than a form). Neither the gradient nor the divergence actually depends on the choice of orientation, and so the Laplace–Beltrami operator itself does not depend on this additional structure.
 (proof)
(proof)
where the last equality is an application of Stokes' theorem
. Dualizing gives
for all compactly supported functions ƒ and h. Conversely, characterizes Δ completely, in the sense that it is the only operator with this property.
As a consequence, the Laplace–Beltrami operator is negative and formally self-adjoint, meaning that for compactly supported functions ƒ and h,

Because the Laplace–Beltrami operator, as defined in this manner, is negative rather than positive, often it is defined with the opposite sign.
associated to the Levi-Civita connection. From this perspective, let Xi be a basis of tangent vector fields (not necessarily induced by a coordinate system). Then the Hessian
of a function f is the symmetric 2-tensor whose components are given by
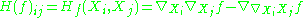
This is easily seen to transform tensorially, since it is linear in each of the arguments Xi, Xj. The Laplace–Beltrami operator is then the trace of the Hessian with respect to the metric:
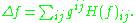
In abstract indices, the operator is often written

provided it is understood implicitly that this trace is in fact the trace of the Hessian tensor.
Because the covariant derivative extends canonically to arbitrary tensor
s, the Laplace–Beltrami operator defined on a tensor T by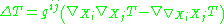
is well-defined.
on sections of the bundle of differential form
s on a pseudo-Riemannian manifold
. On a Riemannian manifold
it is an elliptic operator
, while on a Lorentzian manifold it is hyperbolic. The Laplace–de Rham operator is defined by

where d is the exterior derivative
or differential and δ is the codifferential, acting as on k-forms where ∗ is the Hodge star.
When computing Δƒ for a scalar function ƒ, we have δƒ = 0, so that
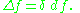
Up to an overall sign, The Laplace–de Rham operator is equivalent to the previous definition of the Laplace–Beltrami operator when acting on a scalar function; see the proof for details. On functions, the Laplace–de Rham operator is actually the negative of the Laplace–Beltrami operator, as the conventional normalization of the codifferential assures that the Laplace–de Rham operator is (formally) positive definite, whereas the Laplace–Beltrami operator is typically negative. The sign is a pure convention, however, and both are common in the literature. The Laplace–de Rham operator differs more significantly from the tensor Laplacian restricted to act on skew-symmetric tensors. Apart from the incidental sign, the two operators differ by a Weitzenböck identity
that explicitly involves the Ricci curvature tensor.
Euclidean space
In the usual (orthonormal) Cartesian coordinates xi on Euclidean space
, the metric is reduced to the Kronecker delta, and one therefore has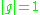 . Consequently, in this case
. Consequently, in this case
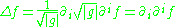
which is the ordinary Laplacian. In curvilinear coordinates
, such as spherical or cylindrical coordinates, one obtains alternative expressions.
Similarly, the Laplace–Beltrami operator corresponding to the Minkowski metric with signature
(+++−) is the D'Alembertian.
Spherical Laplacian
The spherical Laplacian is the Laplace–Beltrami operator on the (n − 1)-sphere with its canonical metric of constant sectional curvature 1. It is convenient to regard the sphere as isometrically embedded into Rn as the unit sphere centred at the origin. Then for a function ƒ on Sn−1, the spherical Laplacian is defined by
where ƒ(x/|x|) is the degree zero homogeneous extension of the function ƒ to Rn − {0}, and Δ is the Laplacian of the ambient Euclidean space. Concretely, this is implied by the well-known formula for the Euclidean Laplacian in spherical polar coordinates: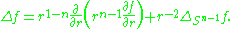
More generally, one can formulate a similar trick using the normal bundle
to define the Laplace–Beltrami operator of any Riemannian manifold isometrically embedded as a hypersurface of Euclidean space.
One can also give an intrinsic description of the Laplace–Beltrami operator on the sphere in a normal coordinate system
. Let (t, ξ) be spherical coordinates on the sphere with respect to a particular point p of the sphere (the "north pole"), that is geodesic polar coordinates with respect to p. Here t represents the latitude measurement along a unit speed geodesic from p, and ξ a parameter representing the choice of direction of the geodesic in Sn−1. Then the spherical Laplacian has the form: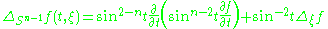
where is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.
is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.
Hyperbolic space
A similar technique works in hyperbolic space
. Here the hyperbolic space Hn−1 can be embedded into the n dimensional Minkowski space
, a real vector space equipped with the quadratic form
Then Hn is the subset of the future null cone in Minkowski space given by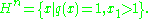
Then
Here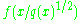 is the degree zero homogeneous extension of f to the interior of the future null cone and □ is the wave operator
is the degree zero homogeneous extension of f to the interior of the future null cone and □ is the wave operator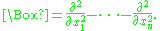
The operator can also be written in polar coordinates. Let (t, ξ) be spherical coordinates on the sphere with respect to a particular point p of Hn−1 (say, the center of the Poincaré disc). Here t represents the hyperbolic distance from p and ξ a parameter representing the choice of direction of the geodesic in Sn−1. Then the spherical Laplacian has the form:
where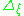 is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.
is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, named after Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
, can be generalized to operate on functions defined on surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and, more generally, on Riemannian
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
and pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s. This more general operator goes by the name Laplace–Beltrami operator, after Laplace and Eugenio Beltrami
Eugenio Beltrami
Eugenio Beltrami was an Italian mathematician notable for his work concerning differential geometry and mathematical physics...
. Like the Laplacian, the Laplace–Beltrami operator is defined as the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, and is a linear operator taking functions into functions. The operator can be extended to operate on tensors as the divergence of the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
. Alternatively, the operator can be generalized to operate on differential forms using the divergence and exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
. The resulting operator is called the Laplace–de Rham operator (named after Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
).
Laplace–Beltrami operator
The Laplace–Beltrami operator, like the Laplacian, is the divergence of the gradient:
An explicit formula in local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
is possible.
Suppose first that M is an oriented Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. The orientation allows one to specify a definite volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
on M, given in an oriented coordinate system xi by
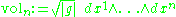
where the dxi are the 1-forms forming the dual basis to the basis vectors
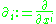
and
 is the wedge product. Here is the absolute value
is the wedge product. Here is the absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
gij. The divergence div X of a vector field X on the manifold is then defined as the scalar function with the property
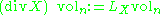
where LX is the Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
along the vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
X. In local coordinates, one obtains
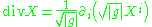
where the Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
is implied, so that the repeated index i is summed over. The gradient of a scalar function ƒ is the vector field grad f that may be defined through the inner product
 on the manifold, as
on the manifold, as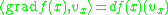
for all vectors vx anchored at point x in the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
TxM of the manifold at point x. Here, dƒ is the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of the function ƒ; it is a 1-form taking argument vx. In local coordinates, one has

where gij are the components of the inverse of the metric tensor, so that with δik the Kronecker delta.
Combining the definitions of the gradient and divergence, the formula for the Laplace–Beltrami operator Δ applied to a scalar function ƒ is, in local coordinates
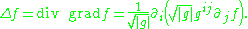
If M is not oriented, then the above calculation carries through exactly as presented, except that the volume form must instead be replaced by a volume element
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
(a density
Density on a manifold
In mathematics, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold which can be integrated in an intrinsic manner. Abstractly, a density is a section of a certain trivial line bundle, called the density bundle...
rather than a form). Neither the gradient nor the divergence actually depends on the choice of orientation, and so the Laplace–Beltrami operator itself does not depend on this additional structure.
Formal self-adjointness
The exterior derivative d and −div are formal adjoints, in the sense that for ƒ a compactly supported function (proof)
(proof)where the last equality is an application of Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
. Dualizing gives
for all compactly supported functions ƒ and h. Conversely, characterizes Δ completely, in the sense that it is the only operator with this property.
As a consequence, the Laplace–Beltrami operator is negative and formally self-adjoint, meaning that for compactly supported functions ƒ and h,

Because the Laplace–Beltrami operator, as defined in this manner, is negative rather than positive, often it is defined with the opposite sign.
Tensor Laplacian
The Laplace–Beltrami operator can be written using the trace of the iterated covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
associated to the Levi-Civita connection. From this perspective, let Xi be a basis of tangent vector fields (not necessarily induced by a coordinate system). Then the Hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of a function f is the symmetric 2-tensor whose components are given by
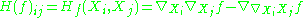
This is easily seen to transform tensorially, since it is linear in each of the arguments Xi, Xj. The Laplace–Beltrami operator is then the trace of the Hessian with respect to the metric:
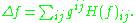
In abstract indices, the operator is often written

provided it is understood implicitly that this trace is in fact the trace of the Hessian tensor.
Because the covariant derivative extends canonically to arbitrary tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s, the Laplace–Beltrami operator defined on a tensor T by
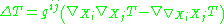
is well-defined.
Laplace–de Rham operator
More generally, one can define a Laplacian differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
on sections of the bundle of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on a pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
. On a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
it is an elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
, while on a Lorentzian manifold it is hyperbolic. The Laplace–de Rham operator is defined by

where d is the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
or differential and δ is the codifferential, acting as on k-forms where ∗ is the Hodge star.
When computing Δƒ for a scalar function ƒ, we have δƒ = 0, so that
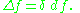
Up to an overall sign, The Laplace–de Rham operator is equivalent to the previous definition of the Laplace–Beltrami operator when acting on a scalar function; see the proof for details. On functions, the Laplace–de Rham operator is actually the negative of the Laplace–Beltrami operator, as the conventional normalization of the codifferential assures that the Laplace–de Rham operator is (formally) positive definite, whereas the Laplace–Beltrami operator is typically negative. The sign is a pure convention, however, and both are common in the literature. The Laplace–de Rham operator differs more significantly from the tensor Laplacian restricted to act on skew-symmetric tensors. Apart from the incidental sign, the two operators differ by a Weitzenböck identity
Weitzenbock identity
In mathematics, in particular in differential geometry, mathematical physics, and representation theory a Weitzenböck identity expresses a relationship between two second-order elliptic operators on a manifold with the same leading symbol...
that explicitly involves the Ricci curvature tensor.
Examples
Many examples of the Laplace–Beltrami operator can be worked out explicitly.Euclidean space
In the usual (orthonormal) Cartesian coordinates xi on Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the metric is reduced to the Kronecker delta, and one therefore has
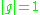 . Consequently, in this case
. Consequently, in this case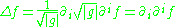
which is the ordinary Laplacian. In curvilinear coordinates
Curvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
, such as spherical or cylindrical coordinates, one obtains alternative expressions.
Similarly, the Laplace–Beltrami operator corresponding to the Minkowski metric with signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(+++−) is the D'Alembertian.
Spherical Laplacian
The spherical Laplacian is the Laplace–Beltrami operator on the (n − 1)-sphere with its canonical metric of constant sectional curvature 1. It is convenient to regard the sphere as isometrically embedded into Rn as the unit sphere centred at the origin. Then for a function ƒ on Sn−1, the spherical Laplacian is defined by

where ƒ(x/|x|) is the degree zero homogeneous extension of the function ƒ to Rn − {0}, and Δ is the Laplacian of the ambient Euclidean space. Concretely, this is implied by the well-known formula for the Euclidean Laplacian in spherical polar coordinates:
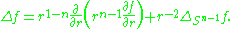
More generally, one can formulate a similar trick using the normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
to define the Laplace–Beltrami operator of any Riemannian manifold isometrically embedded as a hypersurface of Euclidean space.
One can also give an intrinsic description of the Laplace–Beltrami operator on the sphere in a normal coordinate system
Normal coordinates
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p...
. Let (t, ξ) be spherical coordinates on the sphere with respect to a particular point p of the sphere (the "north pole"), that is geodesic polar coordinates with respect to p. Here t represents the latitude measurement along a unit speed geodesic from p, and ξ a parameter representing the choice of direction of the geodesic in Sn−1. Then the spherical Laplacian has the form:
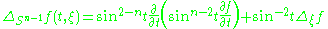
where
 is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.
is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.Hyperbolic space
A similar technique works in hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. Here the hyperbolic space Hn−1 can be embedded into the n dimensional Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, a real vector space equipped with the quadratic form

Then Hn is the subset of the future null cone in Minkowski space given by
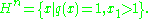
Then

Here
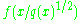 is the degree zero homogeneous extension of f to the interior of the future null cone and □ is the wave operator
is the degree zero homogeneous extension of f to the interior of the future null cone and □ is the wave operator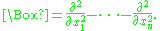
The operator can also be written in polar coordinates. Let (t, ξ) be spherical coordinates on the sphere with respect to a particular point p of Hn−1 (say, the center of the Poincaré disc). Here t represents the hyperbolic distance from p and ξ a parameter representing the choice of direction of the geodesic in Sn−1. Then the spherical Laplacian has the form:

where
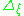 is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.
is the Laplace–Beltrami operator on the ordinary unit (n − 2)-sphere.

