Geometric flow
Encyclopedia
In mathematics
, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold
which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature
. They can be interpreted as flows on a moduli space
(for intrinsic flows) or a parameter space
(for extrinsic flows).
These are of fundamental interest in the calculus of variations
, and include several famous problems and theories.
Particularly interesting are their critical point
s.
A geometric flow is also called a geometric evolution equation.
immersed submanifolds. In general they change both the Riemannian metric and the immersion.
s. A given flow frequently admits all of these interpretations, as follows.
Given an elliptic operator
L, the parabolic PDE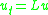
yields a flow, and stationary states for the flow are solutions to the elliptic partial differential equation 
.
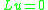If the equation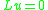
is the Euler-Lagrange equation
for some functional F, then the flow has a variational interpretation as the gradient flow of F, and stationary states of the flow correspond to critical points of the functional.
In the context of geometric flows, the functional is often the L2 norm of some curvature.
Thus, given a curvature K, one can define the functional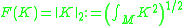
, which has Euler-Lagrange equation 
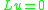for some elliptic operator L, and associated parabolic PDE 
.
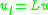The Ricci flow
, Calabi flow
, and Yamabe flow
arise in this way (in some cases with normalizations).
Curvature flows may or may not preserve volume (the Calabi flow does, while the Ricci flow does not), and if not, the flow may simply shrink or grow the manifold, rather than regularizing the metric. Thus one often normalizes the flow, for instance by fixing the volume.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically differential geometry, a geometric flow is the gradient flow associated to a functional on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
which has a geometric interpretation, usually associated with some extrinsic or intrinsic curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. They can be interpreted as flows on a moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
(for intrinsic flows) or a parameter space
Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
(for extrinsic flows).
These are of fundamental interest in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, and include several famous problems and theories.
Particularly interesting are their critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s.
A geometric flow is also called a geometric evolution equation.
Extrinsic
Extrinsic geometric flows are flows on embedded submanifolds, or more generallyimmersed submanifolds. In general they change both the Riemannian metric and the immersion.
- Mean curvature flowMean curvature flowIn the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold . Intuitively, a family of surfaces evolves under mean curvature flow if the velocity of which a point on the surface moves is given by the mean...
, as in soap filmSoap filmSoap films are thin layers of liquid surrounded by air. For example, if two soap bubbles enters in contact, they merged and a thin film is created in between. Thus, foams are composed of a network of films connected by Plateau borders...
s; critical points are minimal surfaceMinimal surfaceIn mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
s - Willmore flow, as in minimax eversionMinimax eversionIn geometry, minimax eversions are a class of sphere eversions, constructed by using half-way models.It is a variational method, and consists of special homotopies ; contrast with Thurston's corrugations, which are generic.The original method of half-way models was not optimal: the regular...
s of spheres - Inverse mean curvature flowInverse mean curvature flowIn the field of differential geometry in mathematics, inverse mean curvature flow is an example of a geometric flow of hypersurfaces a Riemannian manifold...
Intrinsic
Intrinsic geometric flows are flows on the Riemannian metric, independent of any embedding or immersion.- Ricci flowRicci flowIn differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
, as in the Solution of the Poincaré conjecture, and Richard Hamilton'sRichard Hamilton (professor)Richard Streit Hamilton is Davies Professor of mathematics at Columbia University.He received his B.A in 1963 from Yale University and Ph.D. in 1966 from Princeton University. Robert Gunning supervised his thesis...
proof of the Uniformization theoremUniformization theoremIn mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature... - Calabi flowCalabi flowIn differential geometry, the Calabi flow is an intrinsic geometric flow—a process which deforms the metric of a Riemannian manifold—in a manner formally analogous to the way that vibrations are damped and dissipated in a hypothetical curved n-dimensional structural element.The Calabi flow is an...
- Yamabe flowYamabe flowIn differential geometry, the Yamabe flow is an intrinsic geometric flow—a process which deforms the metric of a Riemannian manifold.It is the negative L2-gradient flow of the total scalar curvature, restricted to a given conformal class: it can be interpreted as deforming a Riemannian metric to a...
Classes of flows
Important classes of flows are curvature flows, variational flows (which extremelize some functional), and flows arising as solutions to parabolic partial differential equationParabolic partial differential equation
A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...
s. A given flow frequently admits all of these interpretations, as follows.
Given an elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
L, the parabolic PDE
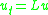yields a flow, and stationary states for the flow are solutions to the elliptic partial differential equation 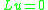.If the equation
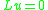is the Euler-Lagrange equationEuler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
for some functional F, then the flow has a variational interpretation as the gradient flow of F, and stationary states of the flow correspond to critical points of the functional.
In the context of geometric flows, the functional is often the L2 norm of some curvature.
Thus, given a curvature K, one can define the functional
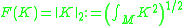, which has Euler-Lagrange equation 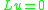for some elliptic operator L, and associated parabolic PDE 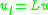.The Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
, Calabi flow
Calabi flow
In differential geometry, the Calabi flow is an intrinsic geometric flow—a process which deforms the metric of a Riemannian manifold—in a manner formally analogous to the way that vibrations are damped and dissipated in a hypothetical curved n-dimensional structural element.The Calabi flow is an...
, and Yamabe flow
Yamabe flow
In differential geometry, the Yamabe flow is an intrinsic geometric flow—a process which deforms the metric of a Riemannian manifold.It is the negative L2-gradient flow of the total scalar curvature, restricted to a given conformal class: it can be interpreted as deforming a Riemannian metric to a...
arise in this way (in some cases with normalizations).
Curvature flows may or may not preserve volume (the Calabi flow does, while the Ricci flow does not), and if not, the flow may simply shrink or grow the manifold, rather than regularizing the metric. Thus one often normalizes the flow, for instance by fixing the volume.