Hermitian symmetric space
Encyclopedia
In mathematics, a Hermitian symmetric space is a Kähler manifold
M which, as a Riemannian manifold
, is a Riemannian symmetric space
. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian. The complex structure is automatically preserved by the isometry group H of the metric, and so M is a homogeneous complex manifold.
Some examples are complex vector space
s and complex projective space
s, with their usual Hermitian metrics and Fubini-Study metric
s, and the complex unit balls with suitable metrics so that they become complete and Riemannian symmetric. The compact
Hermitian symmetric spaces are projective varieties, and admit a strictly larger Lie group
G of biholomorphisms with respect to which they are homogeneous: in fact, they are generalized flag manifolds, i.e., G is semisimple and the stabilizer of a point is a parabolic subgroup P of G. Among (complex) generalized flag manifolds G/P, they are characterized as those for which the nilradical of the Lie algebra of P is abelian. The non-compact Hermitian symmetric spaces can be realized as bounded domains
in complex vector spaces.
Hermitian symmetric spaces are used in the construction of the holomorphic discrete series representation
s of semisimple Lie groups.
In terms of the classification of compact Riemannian symmetric spaces, the Hermitian symmetric spaces are the four infinite series AIII, BDI
with p = 2 or q = 2, DIII and CI, and two exceptional spaces, namely EIII and EVII.
The realization of H/K as a generalized flag variety G/P is obtained by taking G as in the table (a complexification of H) and P equal to the semidirect product of L with the complexified isotropy representation of K, where L (the Levi factor of P) is the complexification of K.
At the Lie algebra
level, there is a symmetric decomposition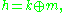
where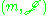
is a real vector space with a complex structure J, whose complex dimension is given in the table. Correspondingly, there is a graded Lie algebra
decomposition
where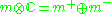
is the decomposition into +i and −i eigenspaces of J and 
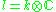. The Lie algebra of P is the semidirect product 
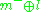. It follows that the exponential image of 
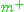modulo P realizes the complex vector space 
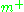as a dense open subset of G/P.
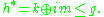
However, whereas the natural map from H/K to G/P is an isomorphism, the natural map from H*/K to G/P is only an injection. In fact its image lies in the exponential image of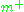
and the corresponding domain in 
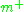is bounded (this is the Harish-Chandra
embedding theorem). The biholomorphism group of H*/K is equal to its isometry group H*.
A bounded domain Ω in a complex vector space (i.e., Ω is an open subset whose closure is compact with respect to the standard topology) is said to be a bounded symmetric domain if for every x in Ω, there is a biholomorphism σx of Ω for which x is an isolated fixed point. Given such a domain Ω, the Bergman kernel
defines a metric on Ω, the Bergman metric
, for which every biholomorphism is an isometry. This realizes Ω as a Hermitian symmetric space of noncompact type.
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
M which, as a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, is a Riemannian symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian. The complex structure is automatically preserved by the isometry group H of the metric, and so M is a homogeneous complex manifold.
Some examples are complex vector space
Complex vector space
A complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
s and complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
s, with their usual Hermitian metrics and Fubini-Study metric
Fubini-Study metric
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....
s, and the complex unit balls with suitable metrics so that they become complete and Riemannian symmetric. The compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hermitian symmetric spaces are projective varieties, and admit a strictly larger Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G of biholomorphisms with respect to which they are homogeneous: in fact, they are generalized flag manifolds, i.e., G is semisimple and the stabilizer of a point is a parabolic subgroup P of G. Among (complex) generalized flag manifolds G/P, they are characterized as those for which the nilradical of the Lie algebra of P is abelian. The non-compact Hermitian symmetric spaces can be realized as bounded domains
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
in complex vector spaces.
Hermitian symmetric spaces are used in the construction of the holomorphic discrete series representation
Holomorphic discrete series representation
In mathematics, a holomorphic discrete series representation is a discrete series representation of a semisimple Lie group that can be represented in a natural way as a Hilbert space of holomorphic functions. The simple Lie groups with holomorphic discrete series are those whose symmetric space is ...
s of semisimple Lie groups.
Compact Hermitian symmetric spaces
The irreducible compact Hermitian symmetric spaces H/K are classified as follows.| G | H | K | complex dimension | geometric interpretation |
|---|---|---|---|---|
 |
 |
 |
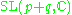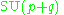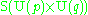pq | Grassmannian Grassmannian In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological... of complex p-dimensional subspaces of  |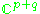
 |
 |
 |
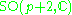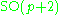p | Grassmannian Grassmannian In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological... of oriented real 2-dimensional subspaces of  |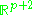
 |
 |
 |
 |
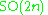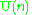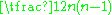Space of orthogonal complex structures on  |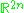
 |
 |
 |
 |
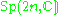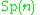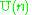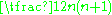Space of complex structures on 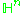 compatible with the inner product |
 |
 |
 |
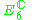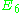16 | Complexification 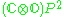 of the Cayley projective plane  |
 |
 |
 |
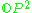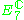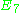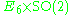27 | Space of symmetric submanifolds of Rosenfeld's projective plane 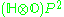 which are isomorphic to  |
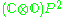In terms of the classification of compact Riemannian symmetric spaces, the Hermitian symmetric spaces are the four infinite series AIII, BDI
with p = 2 or q = 2, DIII and CI, and two exceptional spaces, namely EIII and EVII.
The realization of H/K as a generalized flag variety G/P is obtained by taking G as in the table (a complexification of H) and P equal to the semidirect product of L with the complexified isotropy representation of K, where L (the Levi factor of P) is the complexification of K.
At the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
level, there is a symmetric decomposition
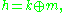
where
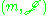is a real vector space with a complex structure J, whose complex dimension is given in the table. Correspondingly, there is a graded Lie algebraGraded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
decomposition
where
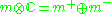is the decomposition into +i and −i eigenspaces of J and 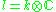. The Lie algebra of P is the semidirect product 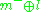. It follows that the exponential image of 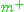modulo P realizes the complex vector space 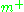as a dense open subset of G/P.Non-compact Hermitian symmetric spaces
As with symmetric spaces in general, each compact Hermitian symmetric space H/K has a noncompact dual H*/K obtained by replacing H with the Lie group H* in G whose Lie algebra is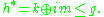However, whereas the natural map from H/K to G/P is an isomorphism, the natural map from H*/K to G/P is only an injection. In fact its image lies in the exponential image of
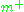and the corresponding domain in 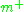is bounded (this is the Harish-ChandraHarish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
embedding theorem). The biholomorphism group of H*/K is equal to its isometry group H*.
A bounded domain Ω in a complex vector space (i.e., Ω is an open subset whose closure is compact with respect to the standard topology) is said to be a bounded symmetric domain if for every x in Ω, there is a biholomorphism σx of Ω for which x is an isolated fixed point. Given such a domain Ω, the Bergman kernel
Bergman kernel
In the mathematical study of several complex variables, the Bergman kernel, named after Stefan Bergman, is a reproducing kernel for the Hilbert space of all square integrable holomorphic functions on a domain D in Cn....
defines a metric on Ω, the Bergman metric
Bergman metric
In differential geometry, the Bergman metric is a Hermitian metric that can be defined on certain types of complex manifold. It is so called because it is derived from the Bergman kernel, both of which are named for Stefan Bergman.-Definition:...
, for which every biholomorphism is an isometry. This realizes Ω as a Hermitian symmetric space of noncompact type.