Partial fractions in complex analysis
Encyclopedia
In complex analysis
, a partial fraction expansion is a way of writing a meromorphic function
f(z) as an infinite sum of rational functions and polynomials. When f(z) is a rational function, this reduces to the usual method of partial fractions.
and the partial fraction technique from algebra, any rational function can be written as a sum of terms of the form 1 / (az + b)k + p(z), where a and b are complex, k is an integer, and p(z) is a polynomial . Just as polynomial factorization
can be generalized to the Weierstrass factorization theorem
, there is an analogy to partial fraction expansions for certain meromorphic functions.
A proper rational function, i.e. one for which the degree of the denominator is greater than the degree of the numerator, has a partial fraction expansion with no polynomial terms. Similarly, a meromorphic function f(z) for which |f(z)| goes to 0 as z goes to infinity at least as quickly as |1/z|, has an expansion with no polynomial terms.
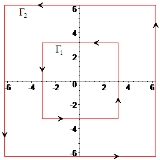
at λ1, λ2, ..., and let (Γ1, Γ2, ...) be a sequence of simple closed curves such that:
Suppose also that there exists an integer p such that
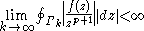
Writing PP(f(z); z = λk) for the principal part
of the Laurent expansion of f about the point λk, we have
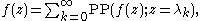
if p = -1, and if p > -1,
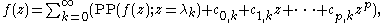
where the coefficients cj,k are given by
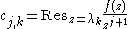
λ0 should be set to 0, because even if f(z) itself does not have a pole at 0, the residue
s of f(z)/zj+1 at z = 0 must still be included in the sum.
Note that in the case of λ0 = 0, we can use the Laurent expansion of f(z) about the origin to get
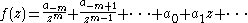
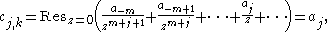
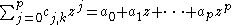
so that the polynomial terms contributed are exactly the regular part of the Laurent series up to zp.
For the other poles λk where k ≥ 1, 1/zj+1 can be pulled out of the residue
calculations:
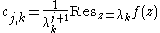
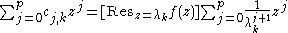
To avoid issues with convergence, the poles should be ordered so that if λk is inside Γn, then λj is also inside Γn for all j < k.
On the horizontal sides of Γk,

so
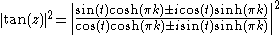
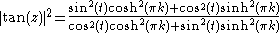
sinh(x) < cosh(x) for all real x, which yields
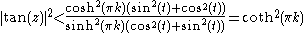
For x > 0, coth(x) is continuous, decreasing, and bounded below by 1, so it follows that on the horizontal sides of Γk, |tan(z)| < coth(π). Similarly, it can be shown that |tan(z)| < 1 on the vertical sides of Γk.
With this bound on |tan(z)| we can see that

(The maximum of |1/z| on Γk occurs at the minimum of |z|, which is kπ).
Therefore p = 0, and the partial fraction expansion of tan(z) looks like

The principal parts and residue
s are easy enough to calculate, as all the poles of tan(z) are simple and have residue -1:
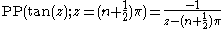
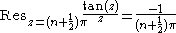
We can ignore λ0 = 0, since both tan(z) and tan(z)/z are analytic at 0, so there is no contribution to the sum, and ordering the poles λk so that λ1 = π/2, λ2 = -π/2, λ3 = 3π/2, etc., gives
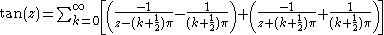
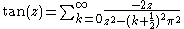
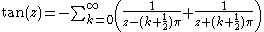
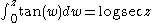
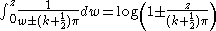
Applying some logarithm rules,
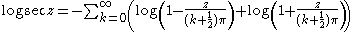
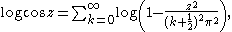
which finally gives
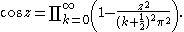
Recall that
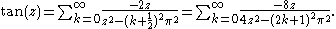
We can expand the summand using a geometric series:
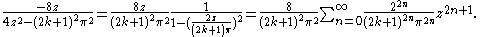
Substituting back,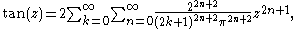
which shows that the coefficients an in the Laurent (Taylor) series of tan(z) about z = 0 are
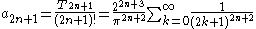
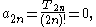
where Tn are the tangent numbers.
Conversely, we can compare this formula to the Taylor expansion for tan(z) about z = 0 to calculate the infinite sums:
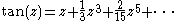
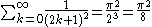
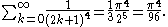
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a partial fraction expansion is a way of writing a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
f(z) as an infinite sum of rational functions and polynomials. When f(z) is a rational function, this reduces to the usual method of partial fractions.
Motivation
By using polynomial long divisionPolynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
and the partial fraction technique from algebra, any rational function can be written as a sum of terms of the form 1 / (az + b)k + p(z), where a and b are complex, k is an integer, and p(z) is a polynomial . Just as polynomial factorization
Polynomial factorization
In mathematics and computer algebra, polynomial factorization refers to factoring a polynomial into irreducible polynomials over a given field.-Formulation of the question:...
can be generalized to the Weierstrass factorization theorem
Weierstrass factorization theorem
In mathematics, the Weierstrass factorization theorem in complex analysis, named after Karl Weierstrass, asserts that entire functions can be represented by a product involving their zeroes...
, there is an analogy to partial fraction expansions for certain meromorphic functions.
A proper rational function, i.e. one for which the degree of the denominator is greater than the degree of the numerator, has a partial fraction expansion with no polynomial terms. Similarly, a meromorphic function f(z) for which |f(z)| goes to 0 as z goes to infinity at least as quickly as |1/z|, has an expansion with no polynomial terms.
Calculation
Let f(z) be a function meromorphic in the finite complex plane with polesPoles
thumb|right|180px|The state flag of [[Poland]] as used by Polish government and diplomatic authoritiesThe Polish people, or Poles , are a nation indigenous to Poland. They are united by the Polish language, which belongs to the historical Lechitic subgroup of West Slavic languages of Central Europe...
at λ1, λ2, ..., and let (Γ1, Γ2, ...) be a sequence of simple closed curves such that:
- The origin lies inside each curve Γk
- No curve passes through a pole of f
- Γk lies inside Γk+1 for all k
-
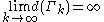 , where d(Γk) gives the distance from the curve to the origin
, where d(Γk) gives the distance from the curve to the origin
Suppose also that there exists an integer p such that
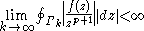
Writing PP(f(z); z = λk) for the principal part
Principal part
In mathematics, the principal part has several independent meanings, but usually refers to the negative-power portion of the Laurent series of a function.-Laurent series definition:...
of the Laurent expansion of f about the point λk, we have
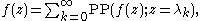
if p = -1, and if p > -1,
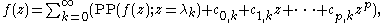
where the coefficients cj,k are given by
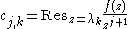
λ0 should be set to 0, because even if f(z) itself does not have a pole at 0, the residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
s of f(z)/zj+1 at z = 0 must still be included in the sum.
Note that in the case of λ0 = 0, we can use the Laurent expansion of f(z) about the origin to get
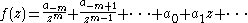
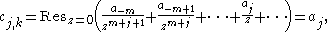
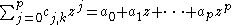
so that the polynomial terms contributed are exactly the regular part of the Laurent series up to zp.
For the other poles λk where k ≥ 1, 1/zj+1 can be pulled out of the residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
calculations:
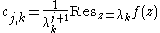
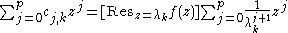
To avoid issues with convergence, the poles should be ordered so that if λk is inside Γn, then λj is also inside Γn for all j < k.
Example
The simplest examples of meromorphic functions with an infinite number of poles are the non-entire trigonometric functions, so take the function tan(z). tan(z) is meromorphic with poles at (n + 1/2)π, n = 0, ±1, ±2, ... The contours Γk will be squares with vertices at ±πk ± πki traversed counterclockwise, k > 1, which are easily seen to satisfy the necessary conditions.On the horizontal sides of Γk,

so
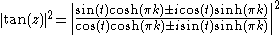
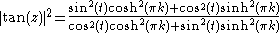
sinh(x) < cosh(x) for all real x, which yields
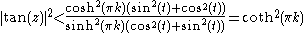
For x > 0, coth(x) is continuous, decreasing, and bounded below by 1, so it follows that on the horizontal sides of Γk, |tan(z)| < coth(π). Similarly, it can be shown that |tan(z)| < 1 on the vertical sides of Γk.
With this bound on |tan(z)| we can see that

(The maximum of |1/z| on Γk occurs at the minimum of |z|, which is kπ).
Therefore p = 0, and the partial fraction expansion of tan(z) looks like

The principal parts and residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
s are easy enough to calculate, as all the poles of tan(z) are simple and have residue -1:
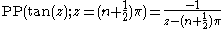
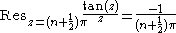
We can ignore λ0 = 0, since both tan(z) and tan(z)/z are analytic at 0, so there is no contribution to the sum, and ordering the poles λk so that λ1 = π/2, λ2 = -π/2, λ3 = 3π/2, etc., gives
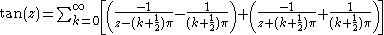
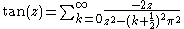
Infinite products
Because the partial fraction expansion often yields sums of 1/(a+bz), it can be useful in finding a way to write a function as an infinite product; integrating both sides gives a sum of logarithms, and exponentiating gives the desired product: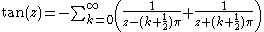
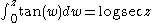
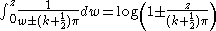
Applying some logarithm rules,
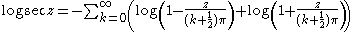
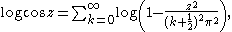
which finally gives
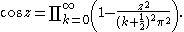
Laurent series
The partial fraction expansion for a function can also be used to find a Laurent series for it by simply replacing the rational functions in the sum with their Laurent series, which are often not difficult to write in closed form. This can also lead to interesting identities if a Laurent series is already known.Recall that
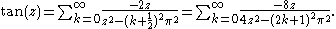
We can expand the summand using a geometric series:
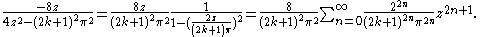
Substituting back,
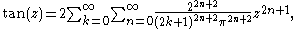
which shows that the coefficients an in the Laurent (Taylor) series of tan(z) about z = 0 are
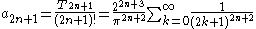
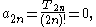
where Tn are the tangent numbers.
Conversely, we can compare this formula to the Taylor expansion for tan(z) about z = 0 to calculate the infinite sums:
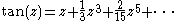
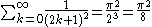
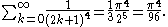
See also
- Partial fractionPartial fractionIn algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function ....
- Line integralLine integralIn mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
- Residue (complex analysis)Residue (complex analysis)In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
- Residue theoremResidue theoremThe residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...

