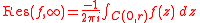Residue at infinity
Encyclopedia
In complex analysis
a branch of mathematics, the residue at infinity is a residue
of a holomorphic function
on an annulus
having an infinite external radius. The infinity is a point added to the local space
is a point added to the local space  in order to render it compact
in order to render it compact
(in this case it is a one-point compactification
). This space noted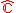 is isomorphic
is isomorphic
to the Riemann sphere
. One can use the residue at infinity to calculate some integral
s.
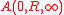 , the residue at infinity of the function f can be defined in terms of the usual residue (mathematics) as follows:
, the residue at infinity of the function f can be defined in terms of the usual residue (mathematics) as follows:
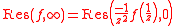
Thus, one can transfer the study of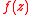 at infinity to the study of
at infinity to the study of 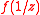 at the origin.
at the origin.
Note that , we have
, we have
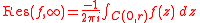
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
a branch of mathematics, the residue at infinity is a residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
of a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on an annulus
Annulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
having an infinite external radius. The infinity
 is a point added to the local space
is a point added to the local space  in order to render it compact
in order to render it compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
(in this case it is a one-point compactification
Alexandroff extension
In mathematical field of topology, the Alexandroff extension is a way to extend a noncompact topological space by adjoining a single point in such a way that the resulting space is compact. It is named for the Russian mathematician Pavel Alexandrov....
). This space noted
 is isomorphic
is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. One can use the residue at infinity to calculate some integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s.
Definition
Given a holomorphic function f on an annulusAnnulus (mathematics)
In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
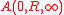 , the residue at infinity of the function f can be defined in terms of the usual residue (mathematics) as follows:
, the residue at infinity of the function f can be defined in terms of the usual residue (mathematics) as follows: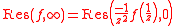
Thus, one can transfer the study of
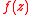 at infinity to the study of
at infinity to the study of 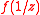 at the origin.
at the origin.Note that
 , we have
, we have