
Isolated singularity
Encyclopedia
In complex analysis
, a branch of mathematics
, an isolated singularity is one that has no other singularities
close to it. In other words, a complex number
z0 is an isolated singularity of a function f if there exists an open
disk
D centered at z0 such that f is holomorphic
on D \ {z0}, that is, on the set obtained from D by taking z0 out.
Formally, and within the general scope of functional analysis
, an isolated singularity for a function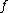 is any topologically isolated point within an open set where the function is defined.
is any topologically isolated point within an open set where the function is defined.
Every singularity of a meromorphic function
is isolated, but isolation of singularities is not alone sufficient to guarantee a function is meromorphic. Many important tools of complex analysis such as Laurent series
and the residue theorem
require that all relevant singularities of the function be isolated.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an isolated singularity is one that has no other singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
close to it. In other words, a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
z0 is an isolated singularity of a function f if there exists an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
D centered at z0 such that f is holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on D \ {z0}, that is, on the set obtained from D by taking z0 out.
Formally, and within the general scope of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, an isolated singularity for a function
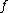 is any topologically isolated point within an open set where the function is defined.
is any topologically isolated point within an open set where the function is defined.Every singularity of a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
is isolated, but isolation of singularities is not alone sufficient to guarantee a function is meromorphic. Many important tools of complex analysis such as Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
and the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
require that all relevant singularities of the function be isolated.
Examples
- The function
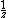 has 0 as an isolated singularity.
has 0 as an isolated singularity.
- The cosecant function
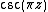 has every integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
has every integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
as an isolated singularity.
Nonisolated singularities
Other than isolated sigularities, complex functions of one variable may exhibit other singular behaviour. Namely, two kinds of nonisolated singularities exist:- Cluster points, i.e. limit points of isolated singularities: if they are all poles, despite admitting Laurent seriesLaurent seriesIn mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
expansions on each of them, no such expansion is possible at its limit.
- Natural boundaries, i.e. any non-isolated set (e.g. a curve) which functions can not be analytically continuedAnalytic continuationIn complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
around (or outside them if they are closed curves in the Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
).
Examples
- The function
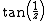 is meromorphic in
is meromorphic in 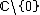 , with simple poles in
, with simple poles in 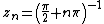 , for every
, for every 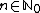 . Since
. Since 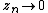 , every punctured disk centred in
, every punctured disk centred in 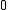 has an infinite number of singularities within, so no Laurent espansion is available for
has an infinite number of singularities within, so no Laurent espansion is available for 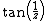 around
around 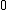 , which is in fact a cluster point of its.
, which is in fact a cluster point of its.
- The function
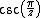 has a singularity at 0 which is not isolated, since there are additional singularities at the reciprocalMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
has a singularity at 0 which is not isolated, since there are additional singularities at the reciprocalMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of every integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
which are located arbitrarily close to 0 (though the singularities at these reciprocals are themselves isolated).
- The function here defined as the Maclaurin series
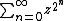 converges inside the unit circle centred in
converges inside the unit circle centred in 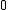 and has it boundarying circumference as natural boundary
and has it boundarying circumference as natural boundary

