Complete theory
Encyclopedia
In mathematical logic
, a theory
is complete if it is a maximal consistent set of sentences, i.e., if it is consistent
, and none of its proper extensions is consistent. For theories in logics which contain classical propositional logic
, this is equivalent to asking that for every sentence
φ in the language
of the theory it contains either φ itself or its negation ¬φ.
Recursively axiomatizable first-order theories that are rich enough to allow general mathematical reasoning to be formulated cannot be complete, as demonstrated by Gödel's incompleteness theorem.
This sense of complete is distinct from the notion of a complete logic, which asserts that for every theory that can be formulated in the logic, all semantically valid statements are provable theorems (for an appropriate sense of "semantically valid"). Gödel's completeness theorem
is about this latter kind of completeness.
Complete theories are closed under a number of conditions internally modelling the T-schema
:
Maximal consistent sets are a fundamental tool in the model theory
of classical logic
and modal logic
. Their existence in a given case is usually a straightforward consequence of Zorn's lemma
, based on the idea that a contradiction
involves use of only finitely many premises. In the case of modal logics, the collection of maximal consistent sets extending a theory T (closed under the necessitation rule) can be given the structure of a model
of T, called the canonical model.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
is complete if it is a maximal consistent set of sentences, i.e., if it is consistent
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
, and none of its proper extensions is consistent. For theories in logics which contain classical propositional logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, this is equivalent to asking that for every sentence
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
φ in the language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of the theory it contains either φ itself or its negation ¬φ.
Recursively axiomatizable first-order theories that are rich enough to allow general mathematical reasoning to be formulated cannot be complete, as demonstrated by Gödel's incompleteness theorem.
This sense of complete is distinct from the notion of a complete logic, which asserts that for every theory that can be formulated in the logic, all semantically valid statements are provable theorems (for an appropriate sense of "semantically valid"). Gödel's completeness theorem
Gödel's completeness theorem
Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. It was first proved by Kurt Gödel in 1929....
is about this latter kind of completeness.
Complete theories are closed under a number of conditions internally modelling the T-schema
T-schema
The T-schema or truth schema is used to give an inductive definition of truth which lies at the heart of any realisation of Alfred Tarski's semantic theory of truth...
:
- For a set
: 
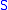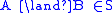if and only if 
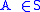and 
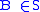, - For a set
: 
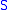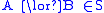if and only if 
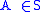or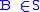 
.
Maximal consistent sets are a fundamental tool in the model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
and modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
. Their existence in a given case is usually a straightforward consequence of Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
, based on the idea that a contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
involves use of only finitely many premises. In the case of modal logics, the collection of maximal consistent sets extending a theory T (closed under the necessitation rule) can be given the structure of a model
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
of T, called the canonical model.
Examples
Some examples of complete theories are:- Presburger arithmeticPresburger arithmeticPresburger arithmetic is the first-order theory of the natural numbers with addition, named in honor of Mojżesz Presburger, who introduced it in 1929. The signature of Presburger arithmetic contains only the addition operation and equality, omitting the multiplication operation entirely...
- Tarski's axiomsTarski's axiomsTarski's axioms, due to Alfred Tarski, are an axiom set for the substantial fragment of Euclidean geometry, called "elementary," that is formulable in first-order logic with identity, and requiring no set theory . Other modern axiomizations of Euclidean geometry are those by Hilbert and George...
for Euclidean geometryEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these... - The theory of dense linear orders
- The theory of algebraically closed fieldAlgebraically closed fieldIn mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
s of a given characteristic - The theory of real closed fieldReal closed fieldIn mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s - Every uncountably categoricalMorley's categoricity theoremIn model theory, a branch of mathematical logic, a theory is κ-categorical if it has exactly one model of cardinality κ up to isomorphism....
countable theory - Every countably categoricalOmega-categorical theoryIn mathematical logic, an omega-categorical theory is a theory that has only one countable model up to isomorphism. Omega-categoricity is the special case κ = \aleph_0 = ω of κ-categoricity, and omega-categorical theories are also referred to as ω-categorical...
countable theory