In the mathematical subject of group theory

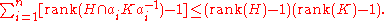
Group theory

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...

, the Hanna Neumann conjecture is a statement about the rank of the intersection of two finitely generated subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s of a free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

. The conjecture was posed by Hanna Neumann

Hanna Neumann

Johanna Neumann was a German-born mathematician who worked on group theory.Johanna was born in Lankwitz, Steglitz-Zehlendorf, Germany. She attended Auguste-Viktoria-Schule and the University of Berlin and completed her studies in 1936 with distinctions in mathematics and physics. She began...

 in 1957. Full solutions have recently been announced independently by Igor Mineyev and Joel Friedman.

History

The subject of the conjecture was originally motivated by a 1954 theorem of Howson who proved that the intersection of any two finitely generated subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s of a free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

 is always finitely generated, that is, has finite rank. In this paper Howson proved that if H and K are subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s of a free group F(X) of finite ranks n ≥ 1 and m ≥ 1 then the rank s of H ∩ K satisfies:

s − 1 ≤ 2mn − m − n.

In a 1956 paper Hanna Neumann

Hanna Neumann

Johanna Neumann was a German-born mathematician who worked on group theory.Johanna was born in Lankwitz, Steglitz-Zehlendorf, Germany. She attended Auguste-Viktoria-Schule and the University of Berlin and completed her studies in 1936 with distinctions in mathematics and physics. She began...

 improved this bound by showing that :

s − 1 ≤ 2mn − 2m − n.

In a 1957 addendum, Hanna Neumann further improved this bound to show that under the above assumptions

s − 1 ≤ 2(m − 1)(n − 1).

She also conjectured that the factor of 2 in the above inequality is not necessary and that one always has

s − 1 ≤ (m − 1)(n − 1).

This statement became known as the Hanna Neumann conjecture.

Formal statement

Let H, K ≤ F(X) be two nontrivial finitely generated subgroups of a free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

 F(X) and let L = H ∩ K be the intersection of H and K. The conjecture says that in this case

rank(L) − 1 ≤ (rank(H) − 1)(rank(K) − 1).

Here for a group G the quantity rank(G) is the rank of G, that is, the smallest size of a generating set

Generating set of a group

In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

 for G.
Every subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

 of a free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

 is known to be free

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

 itself and the rank of a free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

 is equal to the size of any free basis of that free group.

Strengthened Hanna Neumann conjecture

If H, K ≤ G are two subgroups of a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 G and if a, b ∈ G define the same double coset

Double coset

In mathematics, an double coset in G, where G is a group and H and K are subgroups of G, is an equivalence class for the equivalence relation defined on G by...

 HaK = HbK then the subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s H ∩ aKa⁻¹ and H ∩ bKb⁻¹ are conjugate

Conjugacy class

In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...

 in G and thus have the same rank. It is known that if H, K ≤ F(X) are finitely generated subgroups of a finitely generated free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

 F(X) then there exist at most finitely many double coset classes HaK in F(X) such that H ∩ aKa⁻¹ ≠ {1}. Suppose that at least one such double coset exists and let a₁,...,a_n be all the distinct representatives of such double cosets. The strengthened Hanna Neumann conjecture, formulated by Walter Neumann (1990), states that in this situation

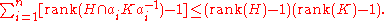
Partial results and other generalizations

• In 1971 Burns improved Hanna Neumann's 1957 bound and proved that under the same assumptions as in Hanna Neumann's paper one has

s ≤ 2mn − 3m − 2n + 4.

• In a 1990 paper, Walter Neumann formulated the strengthened Hanna Neumann conjecture (see statement above).
• Tardos
  Gábor Tardos
  Gábor Tardos is a Hungarian mathematician, currently a professor and Canada Research Chair at Simon Fraser University. He works mainly in combinatorics and computer science...
  
   (1992) established the Hanna Neumann Conjecture for the case where at least one of the subgroups H and K of F(X) has rank two. As most other approaches to the Hanna Neumann conjecture, Tardos used the technique of Stallings subgroup graphs for analyzing subgroups of free groups and their intersections.
• Warren Dicks (1994) established the equivalence of the strengthened Hanna Neumann conjecture and a graph-theoretic statement that he called the amalgamated graph conjecture.
• Arzhantseva (2000) proved that if H is a finitely generated subgroup of infinite index in F(X), then, in a certain statistical meaning, for a generic finitely generated subgroup in 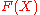, we have H ∩ gKg⁻¹ = {1} for all g in F. Thus, the strengthened Hanna Neumann conjecture holds for every H and a generic K.
• In 2001 Dicks and Formanek used this equivalence to prove the strengthened Hanna Neumann Conjecture in the case when one of the subgroups H and K of F(X) has rank at most three.
• Khan (2002) and, independently, Meakin and Weil (2002), showed that the conclusion of the strengthened Hanna Neumann conjecture holds if one of the subgroups H, K of F(X) is positively generated, that is, generated by a finite set of words that involve only elements of X but not of X⁻¹ as letters.
• Ivanov and, subsequently, Dicks and Ivanov, obtained analogs and generalizations of Hanna Neumann's results for the intersection of subgroup
  Subgroup
  In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
  
  s H and K of a free product
  Free product
  In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
  
   of several groups.
• Wise (2005) showed that the strengthened Hanna Neumann conjecture implies another long-standing group-theoretic conjecture which says that every one-relator group with torsion is coherent (that is, every finitely generated subgroup in such a group is finitely presented).