
Quiver (mathematics)
Encyclopedia
In mathematics
, a quiver is a directed graph
where loops and multiple arrows between two vertices
are allowed, i.e. a multidigraph. They are commonly used in representation theory
: a representation, V, of a quiver assigns a vector space
V(x) to each vertex x of the quiver and a linear map V(a) to each arrow a.
If K is a field
and Γ is a quiver, then the quiver algebra or path algebra KΓ is defined as follows. A path in Γ is a sequence of arrows an an-1 ... a3 a2 a1 such that the head of ai+1 = tail of ai, using the convention of concatenating paths from right to left. Then the path algebra is a vector space having all the paths (of length ≥ 0) in the quiver as basis (including, for each vertex i of the quiver Γ, a trivial path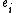 of length 0; these paths are not assumed to be equal for different i), and multiplication given by concatenation of paths. If two paths cannot be concatenated because the end vertex of the first is not equal to the starting vertex of the second, their product is defined to be zero. This defines an associative algebra
of length 0; these paths are not assumed to be equal for different i), and multiplication given by concatenation of paths. If two paths cannot be concatenated because the end vertex of the first is not equal to the starting vertex of the second, their product is defined to be zero. This defines an associative algebra
over K. This algebra has a unit element if and only if the quiver has only finitely many vertices. In this case, the modules
over KΓ are naturally identified with the representations of Γ.
If the quiver has finitely many vertices and arrows, and the end vertex and starting vertex of any path are always distinct (i.e. Q has no oriented cycles), then KΓ is a finite-dimensional hereditary algebra over K.
A morphism, ƒ : V → V' , between representations of the quiver Q, is a collection of linear maps 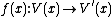 such that for every arrow a in Q from x to y
such that for every arrow a in Q from x to y 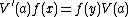 , i.e. the squares that ƒ forms with the arrows of V and V
, i.e. the squares that ƒ forms with the arrows of V and V' all commute. A morphism, ƒ, is an isomorphism, if ƒ(x) is invertible for all vertices x in the quiver. With these definitions the representations of a quiver form a category
.
If V and W are representations of a quiver Q, then the direct sum of these representations,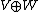 , is defined by
, is defined by 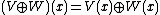 for all vertices x in Q and
for all vertices x in Q and 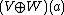 is the direct sum of the linear mappings V(a) and W(a).
is the direct sum of the linear mappings V(a) and W(a).
A representation is said to be decomposable if it is isomorphic to the direct sum of non-zero representations.
A categorical
definition of a quiver representation can also be given. The quiver itself can be considered a category, where the vertices are objects and paths are morphisms. Then a representation of Q is just a covariant functor
from this category to the category of finite dimensional vector space
s. Morphisms of representations of Q are precisely natural transformations between the corresponding functors.
For a finite quiver Γ (a quiver with finitely many vertices and edges), let KΓ be its path algebra. Let ei denote the trivial path at vertex i. Then we can associate to the vertex i, the projective
KΓ module
KΓei consisting of linear combinations of paths which have starting vertex i. This corresponds to the representation of Γ obtained by putting a copy of K at each vertex which lies on a path starting at i and 0 on each other vertex. To each edge joining two copies of K we associate the identity map.
found a generalization of Gabriel's theorem in which all Dynkin diagrams of finite dimensional semisimple Lie algebras occur.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quiver is a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
where loops and multiple arrows between two vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
are allowed, i.e. a multidigraph. They are commonly used in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
: a representation, V, of a quiver assigns a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V(x) to each vertex x of the quiver and a linear map V(a) to each arrow a.
If K is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and Γ is a quiver, then the quiver algebra or path algebra KΓ is defined as follows. A path in Γ is a sequence of arrows an an-1 ... a3 a2 a1 such that the head of ai+1 = tail of ai, using the convention of concatenating paths from right to left. Then the path algebra is a vector space having all the paths (of length ≥ 0) in the quiver as basis (including, for each vertex i of the quiver Γ, a trivial path
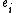 of length 0; these paths are not assumed to be equal for different i), and multiplication given by concatenation of paths. If two paths cannot be concatenated because the end vertex of the first is not equal to the starting vertex of the second, their product is defined to be zero. This defines an associative algebra
of length 0; these paths are not assumed to be equal for different i), and multiplication given by concatenation of paths. If two paths cannot be concatenated because the end vertex of the first is not equal to the starting vertex of the second, their product is defined to be zero. This defines an associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over K. This algebra has a unit element if and only if the quiver has only finitely many vertices. In this case, the modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over KΓ are naturally identified with the representations of Γ.
If the quiver has finitely many vertices and arrows, and the end vertex and starting vertex of any path are always distinct (i.e. Q has no oriented cycles), then KΓ is a finite-dimensional hereditary algebra over K.
Representations of quivers
A representation V of a quiver Q is said to be trivial if V(x) = 0 for all vertices x in Q.A morphism, ƒ : V → V
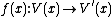 such that for every arrow a in Q from x to y
such that for every arrow a in Q from x to y 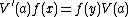 , i.e. the squares that ƒ forms with the arrows of V and V
, i.e. the squares that ƒ forms with the arrows of V and VCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
.
If V and W are representations of a quiver Q, then the direct sum of these representations,
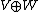 , is defined by
, is defined by 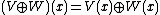 for all vertices x in Q and
for all vertices x in Q and 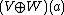 is the direct sum of the linear mappings V(a) and W(a).
is the direct sum of the linear mappings V(a) and W(a).A representation is said to be decomposable if it is isomorphic to the direct sum of non-zero representations.
A categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
definition of a quiver representation can also be given. The quiver itself can be considered a category, where the vertices are objects and paths are morphisms. Then a representation of Q is just a covariant functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from this category to the category of finite dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. Morphisms of representations of Q are precisely natural transformations between the corresponding functors.
For a finite quiver Γ (a quiver with finitely many vertices and edges), let KΓ be its path algebra. Let ei denote the trivial path at vertex i. Then we can associate to the vertex i, the projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
KΓ module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
KΓei consisting of linear combinations of paths which have starting vertex i. This corresponds to the representation of Γ obtained by putting a copy of K at each vertex which lies on a path starting at i and 0 on each other vertex. To each edge joining two copies of K we associate the identity map.
Gabriel's theorem
A quiver is of finite type if it has only finitely many isomorphism classes of indecomposable representations. classified all quivers of finite type, and also their indecomposable representations. More precisely, Gabriel's theorem states that:- A (connected) quiver is of finite type if and only if its underlying graph (when the directions of the arrows are ignored) is one of the ADEADE classificationIn mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
Dynkin diagrams: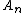 ,
,  ,
,  ,
, 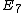 ,
, 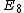 .
. - The indecomposable representations are in a one-to-one correspondence with the positive roots of the root systemRoot systemIn mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
of the Dynkin diagram.
found a generalization of Gabriel's theorem in which all Dynkin diagrams of finite dimensional semisimple Lie algebras occur.
See also
- ADE classificationADE classificationIn mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
- Graph algebraGraph algebraIn mathematics, especially in the fields of universal algebra and graph theory, a graph algebra is a way of giving a directed graph an algebraic structure. It was introduced in , and has seen many uses in the field of universal algebra since then....
- Group algebraGroup algebraIn mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
- Incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
- Quiver diagramQuiver diagramIn physics, a quiver diagram is a graph representing the matter content of a gauge theory that describes D-branes on orbifolds.Each node of the graph corresponds to a factor U of the gauge group, and each link represents a field in the bifundamental representation.The relevance of quiver diagrams...

