
Graph algebra
Encyclopedia
In mathematics
, especially in the fields of universal algebra
and graph theory
, a graph algebra is a way of giving a directed graph
an algebraic structure
. It was introduced in , and has seen many uses in the field of universal algebra since then.
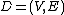 be a directed graph
be a directed graph
, and let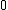 be an element not in
be an element not in 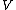 . The graph algebra associated with
. The graph algebra associated with  is the set
is the set 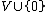 equipped with multiplication defined by the rules
equipped with multiplication defined by the rules  if
if  , and
, and 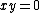 if
if  .
.
in universal algebra
and several other directions of discrete mathematics
and computer science
. Graph algebras have been used, for example, in constructions concerning dualities , equational theories , flatness
, groupoid ring
s , topologies
, varieties
, finite state automata , finite state machine
s ,
tree languages and tree automata etc.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the fields of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a graph algebra is a way of giving a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
. It was introduced in , and has seen many uses in the field of universal algebra since then.
Definition
Let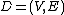 be a directed graph
be a directed graphGraph (data structure)
In computer science, a graph is an abstract data structure that is meant to implement the graph and hypergraph concepts from mathematics.A graph data structure consists of a finite set of ordered pairs, called edges or arcs, of certain entities called nodes or vertices...
, and let
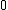 be an element not in
be an element not in 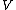 . The graph algebra associated with
. The graph algebra associated with  is the set
is the set 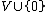 equipped with multiplication defined by the rules
equipped with multiplication defined by the rules  if
if  , and
, and 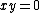 if
if  .
.Applications
This notion has made it possible to use the methods of graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
in universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
and several other directions of discrete mathematics
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. Graph algebras have been used, for example, in constructions concerning dualities , equational theories , flatness
Flatness (systems theory)
Flatness in systems theory is a system property that extends the notion of Controllability from linear systems to nonlinear dynamical systems. A system that has the flatness property is called a flat system. Flat systems have a flat output, which can be used to explicitly express all states and...
, groupoid ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s , topologies
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, varieties
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
, finite state automata , finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
s ,
tree languages and tree automata etc.

