
Gibbs state
Encyclopedia
In probability theory
and statistical mechanics
, a Gibbs state is an equilibrium probability distribution which remains invariant under future evolution of the system. For example, a stationary or steady-state distribution of a Markov chain
, such as that achieved by running a Markov chain Monte Carlo
iteration for a sufficiently long time, is a Gibbs state.
Precisely, suppose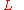 is a generator of evolutions for an initial state
is a generator of evolutions for an initial state  , so that the state at any later time is given by
, so that the state at any later time is given by  . Then the condition for
. Then the condition for  to be a Gibbs state is
to be a Gibbs state is
 .
.
In physics
there may be several physically distinct Gibbs states in which a system may be trapped, particularly at lower temperatures.
They are named after J. Willard Gibbs, for his work in determining equilibrium properties of statistical ensembles.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, a Gibbs state is an equilibrium probability distribution which remains invariant under future evolution of the system. For example, a stationary or steady-state distribution of a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
, such as that achieved by running a Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
iteration for a sufficiently long time, is a Gibbs state.
Precisely, suppose
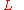 is a generator of evolutions for an initial state
is a generator of evolutions for an initial state  , so that the state at any later time is given by
, so that the state at any later time is given by  . Then the condition for
. Then the condition for  to be a Gibbs state is
to be a Gibbs state is .
.In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
there may be several physically distinct Gibbs states in which a system may be trapped, particularly at lower temperatures.
They are named after J. Willard Gibbs, for his work in determining equilibrium properties of statistical ensembles.

