Periodic graph (crystallography) - AbsoluteAstronomy.com

Crystallography

Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...

, a periodic graph or crystal net is a three dimensional periodic graph

Periodic graph (geometry)

A Euclidean graph is periodic if there exists a basis of that Euclidean space whose corresponding translations induce symmetries of that graph...

, i.e., a three-dimensional

Three-dimensional space

Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...

Euclidean graph

Geometric graph theory

In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs...

whose vertices or nodes are points in three-dimensional Euclidean space

Three-dimensional space

, and whose edges (or bonds or spacers) are line segments connecting pairs of vertices, periodic in three linearly independent axial directions. There is usually an implicit assumption that the set of vertices are uniformly discrete, i.e. that there is a fixed minimum distance between any two vertices. The vertices may represent positions of atoms or complexes or clusters of atoms such as single-metal ion

Ion

An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...

s, molecular building blocks, or secondary building units, while each edge represents a chemical bond

Chemical bond

A chemical bond is an attraction between atoms that allows the formation of chemical substances that contain two or more atoms. The bond is caused by the electromagnetic force attraction between opposite charges, either between electrons and nuclei, or as the result of a dipole attraction...

or a polymer

Polymer

A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...

ic ligand

Ligand

In coordination chemistry, a ligand is an ion or molecule that binds to a central metal atom to form a coordination complex. The bonding between metal and ligand generally involves formal donation of one or more of the ligand's electron pairs. The nature of metal-ligand bonding can range from...

.

Although the notion of a periodic graph or crystal net is ultimately mathematical, and is closely related to that of a Tessellation of space (or honeycomb) in the theory of polytopes and similar areas, much of the contemporary effort in the area is motivated by crystal engineering

Crystal engineering

Crystal engineering is the design and synthesis of molecular solid-state structures with desired properties, based on an understanding and exploitation of intermolecular interactions. The two main strategies currently in use for crystal engineering are based on hydrogen bonding and coordination...

and prediction (design)

Crystal structure prediction

Crystal structure prediction is the calculation of the crystal structures of solids from first principles. Reliable methods of predicting the crystal structure of a compound, based only on its molecular structure, has been a goal of the physical sciences since the 1950s...

, including metal-organic framework

Metal-organic framework

Metal-Organic Frameworks are crystalline compounds consisting of metal ions or clusters coordinated to often rigid organic molecules to form one-, two-, or three-dimensional structures that can be porous. In some cases, the pores are stable to elimination of the guest molecules and can be used for...

s (MOFs) and zeolite

Zeolite

Zeolites are microporous, aluminosilicate minerals commonly used as commercial adsorbents. The term zeolite was originally coined in 1756 by Swedish mineralogist Axel Fredrik Cronstedt, who observed that upon rapidly heating the material stilbite, it produced large amounts of steam from water that...

History

A crystal net is an infinite molecular model

Molecular model

A molecular model, in this article, is a physical model that represents molecules and their processes. The creation of mathematical models of molecular properties and behaviour is molecular modelling, and their graphical depiction is molecular graphics, but these topics are closely linked and each...

of a crystal. Similar models existed in Antiquity

Classical antiquity

Classical antiquity is a broad term for a long period of cultural history centered on the Mediterranean Sea, comprising the interlocking civilizations of ancient Greece and ancient Rome, collectively known as the Greco-Roman world...

, notably the atomic theory associated with Democritus

Democritus

Democritus was an Ancient Greek philosopher born in Abdera, Thrace, Greece. He was an influential pre-Socratic philosopher and pupil of Leucippus, who formulated an atomic theory for the cosmos....

—which was criticized by Aristotle

Aristotle

Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...

as the atomic theory entails a vacuum that nature abhors. But the modern atomic theory

Atomic theory

In chemistry and physics, atomic theory is a theory of the nature of matter, which states that matter is composed of discrete units called atoms, as opposed to the obsolete notion that matter could be divided into any arbitrarily small quantity...

traces back to Johannes Kepler

Johannes Kepler

Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...

and his work on geometric packing problem

Packing problem

Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...

s. Until the Twentieth century, graph-like models of crystals focused on the positions of the (atomic) components, and these pre-20th century models were involved in two controversies in chemistry and materials science.

The two controversies were: the controversy over Robert Boyle

Robert Boyle

Robert Boyle FRS was a 17th century natural philosopher, chemist, physicist, and inventor, also noted for his writings in theology. He has been variously described as English, Irish, or Anglo-Irish, his father having come to Ireland from England during the time of the English plantations of...

’s corpuscular theory of matter, which held that all material substances were composed of particles, and the controversy over whether crystals were minerals or some kind of vegetative phenomenon. During the Eighteenth century, Kepler, Nicolas Steno

Nicolas Steno

Nicolas Steno |Latinized]] to Nicolaus Steno -gen. Nicolai Stenonis-, Italian Niccolo' Stenone) was a Danish pioneer in both anatomy and geology. Already in 1659 he decided not to accept anything simply written in a book, instead resolving to do research himself. He is considered the father of...

, René Just Haüy

René Just Haüy

René Just Haüy – 3 June 1822 in Paris) was a French mineralogist, commonly styled the Abbé Haüy after he was made an honorary canon of Notre Dame. He is often referred to as the "Father of Modern Crystallography." -Biography:...

, and others gradually associated the packing of Boyle-type corpuscular units into arrays with the apparent emergence of polyhedral structures resembling crystals as a result. During the Nineteenth century, there was considerably more work done on polyhedra

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

and also of crystal structure

Crystal structure

In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...

, notably in the derivation of the Crystallographic groups based on the assumption that a crystal could be regarded as a regular array of unit cells. During the early Twentieth century, the physics and chemistry community largely accepted Boyle's corpuscular theory of matter—by now called the atomic theory—and X-ray crystallography was used to determine the position of the atomic or molecular components within the unit cells (by the early Twentieth century, unit cells were regarded as physically meaningful).

However, despite the growing use of stick-and-ball molecular models, the use of graphical edges or line segments to represent chemical bonds in specific crystals have become popular more recently, and the publication of encouraged efforts to determine graphical structures of known crystals, to generate crystal nets of as yet unknown crystals, and to synthesize crystals of these novel crystal nets. The coincident expansion of interest in tilings

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

and tessellations

Honeycomb (geometry)

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....

, especially those modeling quasicrystal

Quasicrystal

A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...

s, and the development of modern Nanotechnology, all facilitated by the dramatic increase in computational power, enabled the development of algorithms from computational geometry

Computational geometry

Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...

for the construction and analysis of crystal nets. Meanwhile, the ancient association between models of crystals and tessellations has expanded with Algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

. There is also a thread of interest in the very-large-scale integration (VLSI) community for using these crystal nets as circuit designs.

Basic formulation

A Euclidean graph

Geometric graph theory

in three-dimensional space is a pair (V, E), where V is a set of points (sometimes called vertices or nodes) and E is a set of edges (sometimes called bonds or spacers), where each edge joins two vertices. There is a tendency in the polyhedral and chemical literature to refer to geometric graphs as nets (contrast with polyhedral nets

Net (polyhedron)

In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...

), and the nomenclature in the chemical literature differs from that of graph theory.

Symmetries and Periodicity

A symmetry of a Euclidean graph is an isometry

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

of the underlying Euclidean space whose restriction to the graph is an automorphism

Graph automorphism

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....

; the symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

of the Euclidean graph is the group of its symmetries. A Euclidean graph in three dimensional Euclidean space is periodic if there exist three linearly independent translations

Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

whose restrictions to the net are symmetries of the net. Often (and always, if one is dealing with a crystal net), the periodic net has finitely many orbits, and is thus uniformly discrete in that there exists a minimum distance between any two vertices.

The result is a three-dimensional periodic graph

Periodic graph (geometry)

A Euclidean graph is periodic if there exists a basis of that Euclidean space whose corresponding translations induce symmetries of that graph...

as a geometric object.

The resulting crystal net will induce a lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

of vectors so that given three vectors that generate

Generating set of a group

In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

the lattice, those three vectors will bound a unit cell, i.e., a parallelopiped which, placed anywhere in space, will enclose a fragment of the net that repeats in the directions of the three axes.

Symmetry and kinds of vertices and edges

Two vertices (or edges) of a periodic graph are symmetric if they are in the same orbit of the symmetry group of the graph; in other words, two vertices (or edges) are symmetric if there is a symmetry of the net that moves one onto the other. In chemistry, there is a tendency to refer to orbits of vertices or edges as “kinds” of vertices or edges, with the recognition that from any two vertices or any two edges (similarly oriented) of the same orbit, the geometric graph “looks the same”. Finite colorings of vertices and edges (where symmetries are to preserve colorings) may be employed.

The symmetry group of a crystal net will be a (group of restrictions of a) crystallographic space group, and many of the most common crystals are of very high symmetry, i.e., very few orbits. A crystal net is uninodal if it has one orbit of vertex (if the vertices were colored

Graph coloring

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...

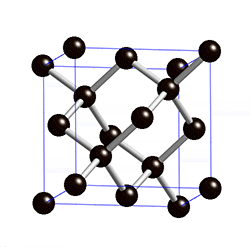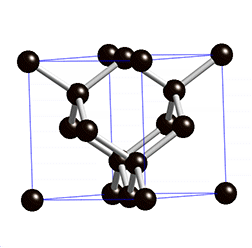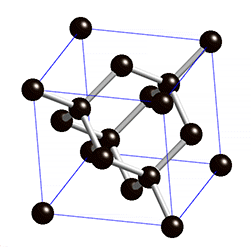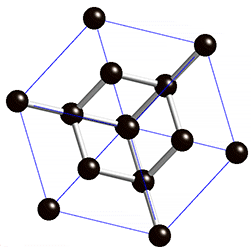
and the symmetries preserve colorings, this would require that a corresponding crystal have atoms of one element or molecular building blocks of one compound – but not vice versa, for it is possible to have a crystal of one element but with several orbits of vertices). Crystals with uninodal crystal nets include cubic diamond

Diamond cubic

The diamond cubic crystal structure is a repeating pattern of 8 atoms that certain materials may adopt as they solidify. While the first known example was diamond, other elements in group IV also adopt this structure, including tin, the semiconductors silicon and germanium, and silicon/germanium...

and some representations of quartz

Quartz

Quartz is the second-most-abundant mineral in the Earth's continental crust, after feldspar. It is made up of a continuous framework of SiO4 silicon–oxygen tetrahedra, with each oxygen being shared between two tetrahedra, giving an overall formula SiO2. There are many different varieties of quartz,...

crystals. Uninodality corresponds with isogonality in geometry and vertex-transitivity

Vertex-transitive graph

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...

in graph theory, and produces examples objective structures. A crystal net is binodal if it has two orbits of vertex; crystals with binodal crystal nets include boracite

Boracite

Boracite is a magnesium borate mineral with formula: Mg3B7O13Cl. It occurs as blue green, colorless, gray, yellow to white crystals in the orthorhombic - pyramidal crystal system. Boracite also shows pseudo-isometric cubical and octahedral forms. These are thought to be the result of transition...

and anatase

Anatase

Anatase is one of the three mineral forms of titanium dioxide, the other two being brookite and rutile. It is always found as small, isolated and sharply developed crystals, and like rutile, a more commonly occurring modification of titanium dioxide, it crystallizes in the tetragonal system; but,...

. It is edge-transitive

Edge-transitive graph

In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....

or isotoxal if it has one orbit of edges; crystals with edge-transitive crystal nets include boracite but not anatase – which has two orbits of edges.

Geometry of Crystal Nets

In the geometry of crystal nets, one can treat edges as line segments. For example, in a crystal net, it is presumed that edges do not “collide” in the sense that when treating them as line segments, they do not intersect. Several polyhedral constructions can be derived from crystal nets. For example, a vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

can be obtained by subdividing

Homeomorphism (graph theory)

In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...

each edge (treated as a line segment) by the insertion of subdividing points, and then the vertex figure of a given vertex is the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

of the adjacent subdividing points (i.e., the convex polyhedron whose vertices are the adjacent subdividing points).

Another polyhedral construction is to determine the neighborhood

Neighbourhood (graph theory)

In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...

of a vertex in the crystal net. One application is to define an energy function as a (possibly weighted) sum of squares of distances from vertices to their neighbors, and with respect to this energy function, the net is in equilibrium (with respect to this energy function) if each vertex is positioned at the centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

of its neighborhood, this is the basis of the crystal net identification program SYSTRE. Some crystal nets are isomorphic to crystal nets in equilibrium positions, and since an equilibrium position is a normal form, the crystal net isomorphism problem (i.e., the query

Query (complexity)

In descriptive complexity, a query is a mapping from structures of one signature to structures of another vocabulary. Neil Immerman, in his book "Descriptive Complexity", "use[s] the concept of query as the fundamental paradigm of computation" ....

whether two given crystal nets are isomorphic as graphs; not to be confused with crystal isomorphism

Isomorphism (crystallography)

In crystallography crystals are described as isomorphous if they are closely similar in shape. Historically crystal shape was defined by measuring the angles between crystal faces with a goniometer...

) is readily computed even though, as a subsumption of the graph isomorphism problem

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

, it is apparently computationally difficult in general.

Active Areas of Crystal Design using Crystal Nets

It is conjectured that crystal nets may minimize entropy

Entropy

Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

in the following sense. Suppose one is given an ensemble of uniformly discrete Euclidean graphs that fill space, with vertices representing atoms or molecular building blocks and with edges representing bonds or ligands, extending through all space to represent a solid. For some restrictions, there may be a unique Euclidean graph that minimizes a reasonably defined energy

Energy

In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...

function, and the conjecture is that that Euclidean graph may necessarily be periodic. This question is still open, but some researchers observe crystal nets of high symmetry tending to predominate observed Euclidean graphs derived from some classes of materials.

Historically, crystals were developed by experimentation, currently formalized as combinatorial chemistry

Combinatorial chemistry

Combinatorial chemistry involves the rapid synthesis or the computer simulation of a large number of different but structurally related molecules or materials...

, but one contemporary desideratum is the synthesis of materials designed in advance, and one proposal is to design crystals (the designs being crystal nets, perhaps represented as one unit cell of a crystal net) and then synthesize them from the design. This effort, in what Omar Yaghi

Omar M. Yaghi

Dr. Omar M. Yaghi is an American chemist, currently the Jean Stone Professor of Chemistry at University of California, Los Angeles. He and his research laboratories design and produce classes of compounds now known as metal-organic frameworks , zeolitic imidazolate frameworks , and covalent...

described as reticular chemistry, is proceeding on several fronts, from the theoretical to synthesizing highly porous crystals.

One of the primary issues in annealing crystals is controlling the constituents, which can be difficult if the constituents are individual atoms, e.g., in zeolites, which are typically porous crystals primarily of silicon and oxygen and occasional impurities. Synthesis of a specific zeolite de novo from a novel crystal net design remains one of the major goals of contemporary research. There are similar efforts in sulfides

Sulfide mineral

The sulfide minerals are a class of minerals containing sulfide as the major anion. Some sulfide minerals are economically important as metal ores. The sulfide class also includes the selenides, the tellurides, the arsenides, the antimonides, the bismuthinides, the sulfarsenides and the sulfosalts...

and phosphates

Phosphate minerals

Phosphate minerals are those minerals that contain the tetrahedrally coordinated phosphate anion along with the freely substituting arsenate and vanadate...

.

Control is more tractable if the constituents are molecular building blocks, i.e., stable molecules that can be readily induced to assemble in accordance with geometric restrictions. Typically, while there may be many species of constituents, there are two main classes: somewhat compact and often polyhedral secondary building units (SBUs), and linking or bridging building units. A popular class of examples are the Metal-Organic Frameworks (MOFs), in which (classically) the secondary building units are metal ion

Ion

s or clusters of ions and the linking building units are organic ligand

Ligand

s. These SBUs and ligands are relatively controllable, and some new crystals have been synthesized using designs of novel nets. An organic variant are the Covalent Organic Frameworks (COFs), in which the SBUs might (but not necessarily) be themselves organic. The greater control over the SBUs and ligands can be seen in the fact that while no novel zeolites have been synthesized per design, several MOFs have been synthesized from crystal nets designed for zeolite synthesis, such as Zeolite-like Metal-Organic Frameworks (Z-MOFs) and zeolitic imidazolate framework (ZIFs).

History

Basic formulation

Symmetries and Periodicity

Symmetry and kinds of vertices and edges

Geometry of Crystal Nets

Active Areas of Crystal Design using Crystal Nets

See also