
Internal angle
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an interior angle (or internal angle) is an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
formed by two sides of a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
that share an endpoint. For a simple, convex or concave polygon, this angle will be an angle on the 'inner side' of the polygon. A polygon has exactly one internal angle per vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
.
If every internal angle of a simple, closed polygon is less than 180°, the polygon is called convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
.
In contrast, an exterior angle (or external angle) is an angle formed by one side of a simple, closed polygon and a line extended from an adjacent side.
The sum of the internal angle and the external angle on the same vertex is 180°.
For example:
x+35+75=180
x+110=180
x=180-110
x=70
The sum of all the internal angles of a simple, closed polygon can be determined by 180(n-2) where n is the number of sides. The formula can by proved using mathematical induction and starting with a triangle for which the angle sum is 180, and then adding a vertex and two sides, etc. A pentagon's internal angles add up to of 540 degrees (shown below)
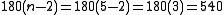
Knowing this you can easily find the measure of each angle if it is a equiangular polygon with
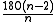 .
.So continuing from the above example with the pentagon:
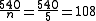
(The exterior angle can be worked out by doing the following sum 360/number of sides in the equiangular polygon
The interior angle can then be found by taking away the value of the exterior angle from 180.
So in a pentagon there are 5 sides so to work out the exterior angle you do 360/5 =72
So the interior angle is 180-72=108 so the interior angle = 108 degrees)
The sum of the external angles of any simple closed (convex or concave) polygon is 360°.
The concept of 'interior angle' can be extended in a consistent way to crossed polygons such as star polygons by using the concept of 'directed angles'. In general, the interior angle sum in degrees of any closed polygon, including crossed (self-intersecting) ones, is then given by 180(n-2k) where n is the number of vertices and k = 0, 1, 2, 3. ... represents the number of total revolutions of 360o one undergoes walking around the perimeter of the polygon, and turning at each vertex, until facing in the same direction one started off from. In other words (or put differently), 360k represents the sum of all the exterior angles. For example, for ordinary convex and concave polygons k = 1, since the exterior angle sum = 360o and one undergoes only one full revolution walking around the perimeter.

