
Covering problem
Encyclopedia
In combinatorics
and computer science
, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that.
Covering problems are minimization problem
s and usually linear programs, whose dual problem
s are called packing problem
s.
The most prominent examples of covering problems are the set cover problem
, which is equivalent to the hitting set problem, and its special cases, the vertex cover problem and the edge cover problem.
, one can think of any linear program as a covering problem if the coefficients in the constraint matrix, the objective function, and right-hand side are nonnegative. More precisely, let us consider the following general integer linear program:
Such an integer linear program is called covering problem if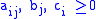 for all
for all 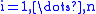 and
and  .
.
Intuition: Assume having types of object and each object of type
types of object and each object of type 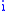 has an associated cost of
has an associated cost of 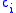 . The number
. The number 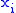 indicates how many objects of type
indicates how many objects of type  we buy. If the constraints
we buy. If the constraints  are satisfied, it is said that
are satisfied, it is said that  is a covering (the structures that are covered depend on the combinatorial context). Finally, an optimal solution to the above integer linear program is a covering of minimal cost.
is a covering (the structures that are covered depend on the combinatorial context). Finally, an optimal solution to the above integer linear program is a covering of minimal cost.
s, for example, the covering problem is defined as the question if for a given marking, there exists a run of the net, such that some larger (or equal) marking can be reached. Larger means here that all components are at least as large as the ones of the given marking and at least one is properly larger.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, covering problems are computational problems that ask whether a certain combinatorial structure 'covers' another, or how large the structure has to be to do that.
Covering problems are minimization problem
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
s and usually linear programs, whose dual problem
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
s are called packing problem
Packing problem
Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...
s.
The most prominent examples of covering problems are the set cover problem
Set cover problem
The set covering problem is a classical question in computer science and complexity theory.It is a problem "whose study has led to the development of fundamental techniques for the entire field" of approximation algorithms...
, which is equivalent to the hitting set problem, and its special cases, the vertex cover problem and the edge cover problem.
General LP formulation
In the context of linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
, one can think of any linear program as a covering problem if the coefficients in the constraint matrix, the objective function, and right-hand side are nonnegative. More precisely, let us consider the following general integer linear program:
| minimize |  |
| subject to | 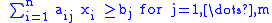 |
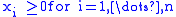 . . |
Such an integer linear program is called covering problem if
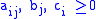 for all
for all 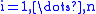 and
and  .
.Intuition: Assume having
 types of object and each object of type
types of object and each object of type 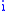 has an associated cost of
has an associated cost of 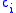 . The number
. The number 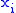 indicates how many objects of type
indicates how many objects of type  we buy. If the constraints
we buy. If the constraints  are satisfied, it is said that
are satisfied, it is said that  is a covering (the structures that are covered depend on the combinatorial context). Finally, an optimal solution to the above integer linear program is a covering of minimal cost.
is a covering (the structures that are covered depend on the combinatorial context). Finally, an optimal solution to the above integer linear program is a covering of minimal cost.Other uses
For Petri netPetri net
A Petri net is one of several mathematical modeling languages for the description of distributed systems. A Petri net is a directed bipartite graph, in which the nodes represent transitions and places...
s, for example, the covering problem is defined as the question if for a given marking, there exists a run of the net, such that some larger (or equal) marking can be reached. Larger means here that all components are at least as large as the ones of the given marking and at least one is properly larger.
See also
- The biclique edge cover problemBipartite dimensionIn the mathematical field of graph theory, the bipartite dimension of a graph G = is the minimum number of bicliques, that is, complete bipartite subgraphs, needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes...
asks for covering all edges of a given graph with (as few as possible) complete bipartite subgraphsComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
.

