In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, tetrahedron packing is the problem of arranging identical regular tetrahedra

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

 throughout three-dimensional space so as to fill the maximum possible fraction of space.
Currently, the best lower bound achieved on the optimal packing fraction of regular tetrahedra is 85.63%. It has been known for hundreds of years that the tetrahedron does not tile

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

 space, but an upper bound below 100% (namely 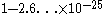) has only recently been reported.
Aristotle

Aristotle

Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...

 claimed that tetrahedra could fill space completely.

In 2006, Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

 and Torquato showed that a packing fraction about 72% can be obtained by constructing a non-Bravais lattice packing of tetrahedra (with multiple particles with generally different orientations per repeating unit), and thus they showed that the best tetrahedron packing cannot be a lattice packing (with one particle per repeating unit such that each particle has a common orientation).