
Cutting stock problem
Encyclopedia
The cutting-stock problem is an optimization
problem, or more specifically, an integer linear programming problem. It arises from many applications in industry. Imagine that you work in a paper mill and you have a number of rolls of paper of fixed width waiting to be cut, yet different customers want different numbers of rolls of various-sized widths. How are you going to cut the rolls so that you minimize the waste (amount of left-overs)?
Solving this problem to optimality can be economically significant: a difference of 1% for a modern paper machine can be worth more than one million USD per year.
 orders, each requiring
orders, each requiring  , j = 1,...,m pieces. We then construct a list of all possible combinations of cuts (often called "patterns"), associating with each pattern a positive integer variable
, j = 1,...,m pieces. We then construct a list of all possible combinations of cuts (often called "patterns"), associating with each pattern a positive integer variable  representing how many times each pattern is to be used. The linear integer program is then:
representing how many times each pattern is to be used. The linear integer program is then:
 , integer
, integer
where is the number of times order
is the number of times order  appears in pattern
appears in pattern  and
and  is the cost (often the waste) of pattern
is the cost (often the waste) of pattern  . The precise nature of the quantity constraints can lead to subtly different mathematical characteristics. The above formulation's quantity constraints are minimum constraints (at least the given amount of each order must be produced, but possibly more). When
. The precise nature of the quantity constraints can lead to subtly different mathematical characteristics. The above formulation's quantity constraints are minimum constraints (at least the given amount of each order must be produced, but possibly more). When  the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the bin packing problem
the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the bin packing problem
. The most general formulation has two-sided constraints (and in this case a minimum-waste solution may consume more than the minimum number of master items):

This formulation applies not just to one-dimensional problems. Many variations are possible, including one where the objective is not to minimise the waste, but to maximise the total value of the produced items, allowing each order to have a different value.
In general, the number of possible patterns grows exponentially as a function of m, the number of orders. As the number of orders increases, it may therefore become impractical to enumerate the possible cutting patterns.
An alternative approach uses delayed column-generation. This method solves the cutting-stock problem by starting with just a few patterns. It generates additional patterns when they are needed. For the one-dimensional case, the new patterns are introduced by solving an auxiliary optimization problem called the knapsack problem
, using dual variable information from the linear program. The knapsack problem has well-known methods to solve it, such as branch and bound
and dynamic programming
. The Delayed Column Generation method can be much more efficient than the original approach, particularly as the size of the problem grows. The column generation approach as applied to the cutting stock problem was pioneered by Gilmore and Gomory in a series of papers published in the 1960s. Gilmore and Gomory showed that this approach is guaranteed to converge to the (fractional) optimal solution, without needing to enumerate all the possible patterns in advance.
A limitation of the original Gilmore and Gomory method is that it does not handle integrality, so the solution may contain fractions, e.g. a particular pattern should be produced 3.67 times. Rounding to the nearest integer often does not work, in the sense that it may lead to a sub-optimal solution and/or under- or over-production of some of the orders (and possible infeasibility in the presence of two-sided demand constraints). This limitation is overcome in modern algorithms, which can solve to optimality (in the sense of finding solutions with minimum waste) very large instances of the problem (generally larger than encountered in practice).
The cutting-stock problem is often highly degenerate, in that multiple solutions with the same waste are possible. This degeneracy arises because it is possible to move items around, creating new patterns, without affecting the waste. This give arise to a whole collection of related problems which are concerned with some other criterion, such as the following:
|-
! width="80pt" | Width
! width="80pt" | Rolls
|-
| align=center | 1380 || align=center | 22
|-
| align=center | 1520 || align=center | 25
|-
| align=center | 1560 || align=center | 12
|-
| align=center | 1710 || align=center | 14
|-
| align=center | 1820 || align=center | 18
|-
| align=center | 1880 || align=center | 18
|-
| align=center | 1930 || align=center | 20
|-
| align=center | 2000 || align=center | 10
|-
| align=center | 2050 || align=center | 12
|-
| align=center | 2100 || align=center | 14
|-
| align=center | 2140 || align=center | 16
|-
| align=center | 2150 || align=center | 18
|-
| align=center | 2200 || align=center | 20
|}
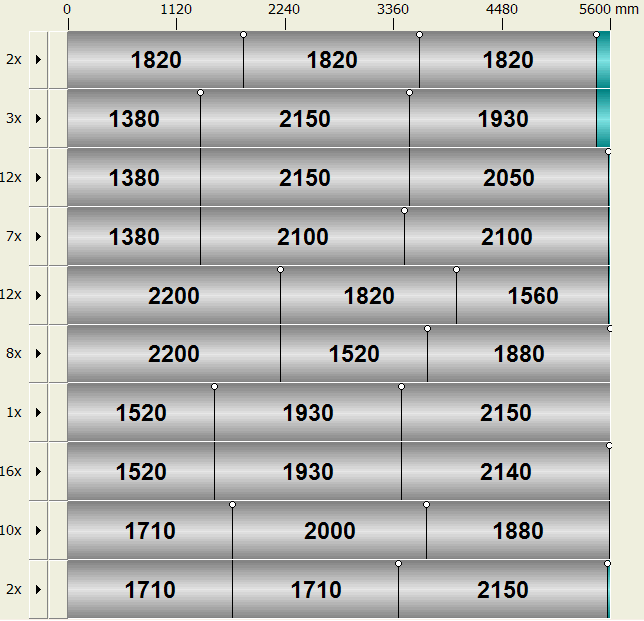 There are 308 possible patterns for this small instance. The optimal answer requires 73 master rolls and has 0.401% waste; it can be shown computationally that in this case the minimum number of patterns with this level of waste is 10. It can also be computed that 19 different such solutions exist, each with 10 patterns and a waste of 0.401%, of which one such solution is shown below and in the picture:
There are 308 possible patterns for this small instance. The optimal answer requires 73 master rolls and has 0.401% waste; it can be shown computationally that in this case the minimum number of patterns with this level of waste is 10. It can also be computed that 19 different such solutions exist, each with 10 patterns and a waste of 0.401%, of which one such solution is shown below and in the picture:
has many industrial applications, such as packing objects into shipping containers (see e.g. containerization
- the related sphere packing
problem has been studied since the 17th century (Kepler conjecture
)).
Suppliers of software that solve the cutting-stock problem for the paper industry include ABB Group, Greycon
, Honeywell
, and Tieto.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
problem, or more specifically, an integer linear programming problem. It arises from many applications in industry. Imagine that you work in a paper mill and you have a number of rolls of paper of fixed width waiting to be cut, yet different customers want different numbers of rolls of various-sized widths. How are you going to cut the rolls so that you minimize the waste (amount of left-overs)?
Solving this problem to optimality can be economically significant: a difference of 1% for a modern paper machine can be worth more than one million USD per year.
Formulation and solution approaches
The standard formulation for the cutting-stock problem (but not the only one) starts with a list of orders, each requiring
orders, each requiring  , j = 1,...,m pieces. We then construct a list of all possible combinations of cuts (often called "patterns"), associating with each pattern a positive integer variable
, j = 1,...,m pieces. We then construct a list of all possible combinations of cuts (often called "patterns"), associating with each pattern a positive integer variable  representing how many times each pattern is to be used. The linear integer program is then:
representing how many times each pattern is to be used. The linear integer program is then:- minimize

- subject to
 and
and
 , integer
, integerwhere
 is the number of times order
is the number of times order  appears in pattern
appears in pattern  and
and  is the cost (often the waste) of pattern
is the cost (often the waste) of pattern  . The precise nature of the quantity constraints can lead to subtly different mathematical characteristics. The above formulation's quantity constraints are minimum constraints (at least the given amount of each order must be produced, but possibly more). When
. The precise nature of the quantity constraints can lead to subtly different mathematical characteristics. The above formulation's quantity constraints are minimum constraints (at least the given amount of each order must be produced, but possibly more). When  the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the bin packing problem
the objective minimises the number of utilised master items and, if the constraint for the quantity to be produced is replaced by equality, it is called the bin packing problemBin packing problem
In computational complexity theory, the bin packing problem is a combinatorial NP-hard problem. In it, objects of different volumes must be packed into a finite number of bins of capacity V in a way that minimizes the number of bins used....
. The most general formulation has two-sided constraints (and in this case a minimum-waste solution may consume more than the minimum number of master items):

This formulation applies not just to one-dimensional problems. Many variations are possible, including one where the objective is not to minimise the waste, but to maximise the total value of the produced items, allowing each order to have a different value.
In general, the number of possible patterns grows exponentially as a function of m, the number of orders. As the number of orders increases, it may therefore become impractical to enumerate the possible cutting patterns.
An alternative approach uses delayed column-generation. This method solves the cutting-stock problem by starting with just a few patterns. It generates additional patterns when they are needed. For the one-dimensional case, the new patterns are introduced by solving an auxiliary optimization problem called the knapsack problem
Knapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
, using dual variable information from the linear program. The knapsack problem has well-known methods to solve it, such as branch and bound
Branch and bound
Branch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
and dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
. The Delayed Column Generation method can be much more efficient than the original approach, particularly as the size of the problem grows. The column generation approach as applied to the cutting stock problem was pioneered by Gilmore and Gomory in a series of papers published in the 1960s. Gilmore and Gomory showed that this approach is guaranteed to converge to the (fractional) optimal solution, without needing to enumerate all the possible patterns in advance.
A limitation of the original Gilmore and Gomory method is that it does not handle integrality, so the solution may contain fractions, e.g. a particular pattern should be produced 3.67 times. Rounding to the nearest integer often does not work, in the sense that it may lead to a sub-optimal solution and/or under- or over-production of some of the orders (and possible infeasibility in the presence of two-sided demand constraints). This limitation is overcome in modern algorithms, which can solve to optimality (in the sense of finding solutions with minimum waste) very large instances of the problem (generally larger than encountered in practice).
The cutting-stock problem is often highly degenerate, in that multiple solutions with the same waste are possible. This degeneracy arises because it is possible to move items around, creating new patterns, without affecting the waste. This give arise to a whole collection of related problems which are concerned with some other criterion, such as the following:
- The minimum pattern count problem: to find a minimum-pattern-count solution amongst the minimum-waste solutions. This is a very hard problem, even when the waste is known. There is a conjectureConjectureA conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
that any equality-constrained one-dimensional instance with n orders has at least one minimum waste solution with no more than n + 1 patterns. No upper bound to the number of patterns is known either, examples with n + 5 are known.
- The minimum stack problem: this is concerned with the sequencing of the patterns so as not to have too many partially completed orders at any time. This was an open problem until 2007, when an efficient algorithm based on dynamic programming was published.
- The minimum number of knife changes problem (for the one-dimensional problem): this is concerned with sequencing and permuting the patterns so as to minimise the number of times the slitting knives have to be moved. This is a special case of the generalised travelling salesman problemTravelling salesman problemThe travelling salesman problem is an NP-hard problem in combinatorial optimization studied in operations research and theoretical computer science. Given a list of cities and their pairwise distances, the task is to find the shortest possible tour that visits each city exactly once...
.
Illustration of one-dimensional cutting-stock problem
A paper machine can produce an unlimited number of master (jumbo) rolls, each 5600 mm wide. The following 13 items must be cut:-
- {| class="wikitable"
|-
! width="80pt" | Width
! width="80pt" | Rolls
|-
| align=center | 1380 || align=center | 22
|-
| align=center | 1520 || align=center | 25
|-
| align=center | 1560 || align=center | 12
|-
| align=center | 1710 || align=center | 14
|-
| align=center | 1820 || align=center | 18
|-
| align=center | 1880 || align=center | 18
|-
| align=center | 1930 || align=center | 20
|-
| align=center | 2000 || align=center | 10
|-
| align=center | 2050 || align=center | 12
|-
| align=center | 2100 || align=center | 14
|-
| align=center | 2140 || align=center | 16
|-
| align=center | 2150 || align=center | 18
|-
| align=center | 2200 || align=center | 20
|}
Solution

| Repetition | Contents |
|---|---|
| 2 | 1820 + 1820 + 1820 |
| 3 | 1380 + 2150 + 1930 |
| 12 | 1380 + 2150 + 2050 |
| 7 | 1380 + 2100 + 2100 |
| 12 | 2200 + 1820 + 1560 |
| 8 | 2200 + 1520 + 1880 |
| 1 | 1520 + 1930 + 2150 |
| 16 | 1520 + 1930 + 2140 |
| 10 | 1710 + 2000 + 1880 |
| 2 | 1710 + 1710 + 2150 |
| 73 |
Classification
Cutting-stock problems can be classified in several ways. One way is the dimensionality of the cutting: the above example illustrates a one-dimensional (1D) problem; other industrial applications of 1D occur when cutting pipes, cables, and steel bars. Two-dimensional (2D) problems are encountered in furniture, clothing and glass production. Not many three-dimensional (3D) applications involving cutting are known; however the closely related 3D packing problemPacking problem
Packing problems are a class of optimization problems in mathematics which involve attempting to pack objects together , as densely as possible. Many of these problems can be related to real life packaging, storage and transportation issues...
has many industrial applications, such as packing objects into shipping containers (see e.g. containerization
Containerization
Containerization is a system of freight transport based on a range of steel intermodal containers...
- the related sphere packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
problem has been studied since the 17th century (Kepler conjecture
Kepler conjecture
The Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
)).
Cutting-stock problem in paper, film and metal industries
Industrial applications of cutting-stock problems for high production volumes arise especially when basic material is produced in large rolls that are further cut into smaller units. This is done e.g. in paper and plastic film industries but also in production of flat metals like steel or brass. There are many variants and additional constraints arising form special production constraints due to machinery and process limits, customer requirements and quality issues; some examples are:- Two-stage, where the rolls produced in the first stage are then processed a second time. For instance, all office stationery (e.g. A4 size in Europe, Letter sizeLetter (paper size)Letter or US Letter is the most common paper size for office use in several countries, including the United States, Canada, Mexico, Bolivia, Colombia, Venezuela, the Philippines, and Chile. It measures 8.5 by 11 inches ....
in US) is produced in such a process. The complication arises because the machinery in the second stage is narrower than the primary. Efficient utilisation of both stages of production is important (from an energy or material use perspective) and what is efficient for the primary stage may be inefficient for the secondary, leading to trade-offs. Metallised filmMetallised filmMetallised films are polymer films coated with a thin layer of metal, usually aluminium. They offer the glossy metallic appearance of an aluminium foil at a reduced weight and cost...
(used in packaging of snacks), and plastic extrusion on paper (used in liquid packagingLiquid packaging boardLiquid packaging board is a multi-ply paperboard with high stiffness, strong wet sizing and a high barrier coating. Only virgin paper fibers are used. The barrier coating must hold the liquid and prevent migration of air and flavors through the paperboard....
, e.g. juice cartons) are further examples of such a process.
- Winder constraints where the slitting process has physical or logical constraints: a very common constraint is that only a certain number of slitting knives are available, so that feasible patterns should not contain more than a maximum number of rolls. Because winder machinery is not standardised, very many other constraints are encountered.
- An example of a customer requirement is when a particular order cannot be satisfied from either of the two edge positions: this is because the edges of the sheet tend to have greater variations in thickness and some applications can be very sensitive to these.
- An example of a quality issue is when the master roll contains defects that have to be cut around. Expensive materials with demanding quality characteristics such as photographic paperPhotographic paperPhotographic paper is paper coated with light-sensitive chemicals, used for making photographic prints.Photographic paper is exposed to light in a controlled manner, either by placing a negative in contact with the paper directly to produce a contact print, by using an enlarger in order to create a...
or TyvekTyvekTyvek is a brand of flashspun high-density polyethylene fibers, a synthetic material; the name is a registered trademark of DuPont. The material is very strong; it is difficult to tear but can easily be cut with scissors or a knife...
have to be carefully optimised so that the wasted area is minimised.
- Multi-machine problems arise when orders can be produced on more than one machine and these machines have different widths. Generally availability of more than one master roll width improves the waste considerably; in practice however additional order splitting constraints may have to be taken into account.
- There is also a semi-continuous problem, where the produced rolls do not have to be of the same diameter, but can vary within a range. This typically occurs with sheet orders. This is sometimes known as a 1½ dimensional problem. This variant also occurs in the production of corrugated fiberboard, where it is known, somewhat confusingly, as the corrugator scheduling problem.
Suppliers of software that solve the cutting-stock problem for the paper industry include ABB Group, Greycon
Greycon
Greycon Ltd is an information technology firm based in London, England developing software for scheduling and the cutting stock problem primarily for the paper, film and nonwovens industries. The company's solution for the cutting stock problem is responsible for savings equivalent to 0.5 – 1.5%...
, Honeywell
Honeywell
Honeywell International, Inc. is a major conglomerate company that produces a variety of consumer products, engineering services, and aerospace systems for a wide variety of customers, from private consumers to major corporations and governments....
, and Tieto.
History
The cutting stock problem was first formulated by Kantorovich in 1939. In 1951 before computers became widely available, L. V. Kantorovich and V. A. Zalgaller suggested solving the problem of the economical use of material at the cutting stage with the help of linear programming. The proposed technique was later called the Column Generation method.Further reading
- Hatem Ben Amor, J.M. Valério de Carvalho, Cutting Stock Problems in Column Generation, edited by Guy Desaulniers, Jacques Desrosiers, and Marius M. Solomon, Springer, 2005, XVI, ISBN 0-387-25485-4

