Flight dynamics
Overview
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
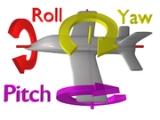
vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions
Dimensions
Dimensions is a French project that makes educational movies about mathematics, focusing on spatial geometry. It uses POV-Ray to render some of the animations, and the films are release under a Creative Commons licence....
about the vehicle's center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
, known as pitch, roll and yaw (quite different from their use as Tait-Bryan angles).
Aerospace engineers develop control system
Control system
A control system is a device, or set of devices to manage, command, direct or regulate the behavior of other devices or system.There are two common classes of control systems, with many variations and combinations: logic or sequential controls, and feedback or linear controls...
s for a vehicle's orientation (attitude) about its center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
.

