Non-linear sigma model
Encyclopedia
In quantum field theory
, a nonlinear σ model describes a scalar field
Σ which takes on values in a nonlinear manifold called the target manifold T.
The target manifold is equipped with a Riemannian metric g. Σ is a differentiable map from Minkowski space
M (or some other space) to T. The Lagrangian density is given by:
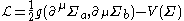
where here, we have used a + - - - metric signature
and the partial derivative
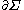is given by a section of the jet bundle
of T×M and V is the potential.
In the coordinate notation, with the coordinates Σa, a=1,...,n where n is the dimension of T,
.
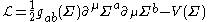In more than 2 dimensions, nonlinear σ models are nonrenormalizable. This means they can only arise as effective field theories
. New physics is needed at around the distance scale where the two point connected correlation function is of the same order as the curvature of the target manifold. This is called the UV completion
of the theory.
There is a special class of nonlinear σ models with the internal symmetry group G *. If G is a Lie group
and H is a Lie subgroup
, then the quotient space
G/H is a manifold (subject to certain technical restrictions like H being a closed subset) and is also a homogeneous space
of G or in other words, a nonlinear realization of G. In many cases, G/H can be equipped with a Riemannian metric which is G-invariant. This is always the case, for example, if G is compact
. A nonlinear σ model with G/H as the target manifold with a G-invariant Riemannian metric and a zero potential is called a quotient space (or coset space) nonlinear σ model.
When computing path integrals
, the functional measure needs to be "weighted" by the square root of the determinant
of g
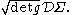
This model proved to be relevant in string theory where the two-dimensional manifold is named worldsheet. Proof of renormalizability was given by Daniel Friedan
. He showed that the theory admits a renormalization group equation, at the leading order of perturbation theory, in the form
being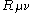
the Ricci tensor. This represents a Ricci flow
having Einstein equations for the target manifold as a fixed point. The existence of such a fixed point is relevant as it grants, at this order of perturbation theory, that conformal invariance
is not lost due to quantum corrections and one has a sensible quantum field theory
.
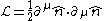
where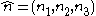
with the constraint 
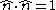and 
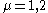. This model allows for topological finite action solutions, as at infinite space-time the Lagrange density must vanish, meaning 
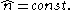at infinity. Therefore in the class of finite-action solutions we may identify the point at the infinity as a single point, i.e. that space-time can be identified with a Riemann Sphere
. Since the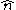
-field lives on a sphere as well, we have a mapping 
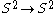, the solutions of which are classified by the Second Homotopy group
of a 2-sphere. These solutions are called the O(3) Instantons.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a nonlinear σ model describes a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
Σ which takes on values in a nonlinear manifold called the target manifold T.
The target manifold is equipped with a Riemannian metric g. Σ is a differentiable map from Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
M (or some other space) to T. The Lagrangian density is given by:
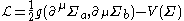
where here, we have used a + - - - metric signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
and the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
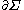is given by a section of the jet bundleJet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
of T×M and V is the potential.
In the coordinate notation, with the coordinates Σa, a=1,...,n where n is the dimension of T,
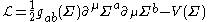.In more than 2 dimensions, nonlinear σ models are nonrenormalizable. This means they can only arise as effective field theories
Effective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
. New physics is needed at around the distance scale where the two point connected correlation function is of the same order as the curvature of the target manifold. This is called the UV completion
UV Completion
In theoretical physics, ultraviolet completion, or UV completion, of a quantum field theory is the passing from a lower energy quantum field theory to a more general quantum field theory above a threshold value known as the cutoff...
of the theory.
There is a special class of nonlinear σ models with the internal symmetry group G *. If G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and H is a Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
, then the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
G/H is a manifold (subject to certain technical restrictions like H being a closed subset) and is also a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
of G or in other words, a nonlinear realization of G. In many cases, G/H can be equipped with a Riemannian metric which is G-invariant. This is always the case, for example, if G is compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
. A nonlinear σ model with G/H as the target manifold with a G-invariant Riemannian metric and a zero potential is called a quotient space (or coset space) nonlinear σ model.
When computing path integrals
Functional integration
Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions...
, the functional measure needs to be "weighted" by the square root of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of g
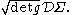
This model proved to be relevant in string theory where the two-dimensional manifold is named worldsheet. Proof of renormalizability was given by Daniel Friedan
Daniel Friedan
Daniel Harry Friedan is an American theoretical physicist and is one of two sons of the feminist author and activist Betty Friedan. He earned his Ph.D...
. He showed that the theory admits a renormalization group equation, at the leading order of perturbation theory, in the form
being
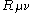the Ricci tensor. This represents a Ricci flowRicci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
having Einstein equations for the target manifold as a fixed point. The existence of such a fixed point is relevant as it grants, at this order of perturbation theory, that conformal invariance
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
is not lost due to quantum corrections and one has a sensible quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
O(3) Non-linear Sigma Model
One of the most famous examples, of interest in for its particularly interesting topological properties, is the O(3) nonlinear sigma model in 1+1 dimension, with the Lagrange density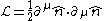where
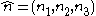with the constraint 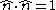and 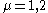. This model allows for topological finite action solutions, as at infinite space-time the Lagrange density must vanish, meaning 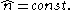at infinity. Therefore in the class of finite-action solutions we may identify the point at the infinity as a single point, i.e. that space-time can be identified with a Riemann SphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Since the
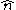-field lives on a sphere as well, we have a mapping 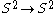, the solutions of which are classified by the Second Homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
of a 2-sphere. These solutions are called the O(3) Instantons.
See also
- Sigma model
- Chiral modelChiral modelIn nuclear physics, the chiral model is a phenomenological model describing mesons in the chiral limit where the masses of the quarks go to zero . It's a nonlinear sigma model with the principal homogeneous space of the Lie group SU as its target manifold where N is the number of quark flavors...
- Little HiggsLittle HiggsIn particle physics, little Higgs models are based on the idea that the Higgs boson is a pseudo-Goldstone boson arising from some global symmetry breaking at a TeV energy scale...
- SkyrmionSkyrmionIn theoretical physics, a skyrmion is a mathematical model used to model baryons . It was conceived by Tony Skyrme.-Overview:...
, a soliton in non-linear sigma models - WZW model
- Fubini-Study metricFubini-Study metricIn mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....
, a metric often used with non-linear sigma models. - Ricci flowRicci flowIn differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
- Scale invarianceScale invarianceIn physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...