
Dense graph
Encyclopedia
In mathematics
, a dense graph is a graph
in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph. The distinction between sparse and dense graphs is rather vague, and depends on the context.
For undirected simple graphs, the graph density is defined as: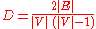
The maximum number of edges is ½ |V| (|V|−1), so the maximal density is 1 (for complete graph
s) and the minimal density is 0 .
of the values α such that the finite subgraphs of G with density α have a bounded number of vertices. It can be shown using the Erdős-Stone theorem that the upper density can only be 1 or one of the superparticular ratios 0, 1/2, 2/3, 3/4, 4/5, ... n/(n + 1), ... (see, e.g., Diestel, p. 189).
are exactly the (1,1)-tight graphs, forests are exactly the (1,1)-sparse graphs, and graphs with arboricity
k are exactly the (k,k)-sparse graphs. Pseudoforest
s are exactly the (1,0)-sparse graphs, and the Laman graph
s arising in rigidity theory are exactly the (2,3)-tight graphs.
Other graph families not characterized by their sparsity can also be described in this way. For instance the facts that any planar graph
with n vertices has at most 3n - 6 edges, and that any subgraph of a planar graph is planar, together imply that the planar graphs are (3,6)-sparse. However, not every (3,6)-sparse graph is planar. Similarly, outerplanar graph
s are (2,3)-sparse and planar bipartite graph
s are (2,4)-sparse.
Streinu and Theran show that testing (k,l)-sparsity may be performed in polynomial time.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dense graph is a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph. The distinction between sparse and dense graphs is rather vague, and depends on the context.
For undirected simple graphs, the graph density is defined as:
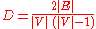
The maximum number of edges is ½ |V| (|V|−1), so the maximal density is 1 (for complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s) and the minimal density is 0 .
Upper density
Upper density is an extension of the concept of graph density defined above from finite graphs to infinite graphs. Intuitively, an infinite graph has arbitrarily large finite subgraphs with any density less than its upper density, and does not have arbitrarily large finite subgraphs with density greater than its upper density. Formally, the upper density of a graph G is the infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of the values α such that the finite subgraphs of G with density α have a bounded number of vertices. It can be shown using the Erdős-Stone theorem that the upper density can only be 1 or one of the superparticular ratios 0, 1/2, 2/3, 3/4, 4/5, ... n/(n + 1), ... (see, e.g., Diestel, p. 189).
Sparse and tight graphs
define a graph as being (k,l)-sparse if every nonempty subgraph with n vertices has at most kn − l edges, and (k,l)-tight if it is (k,l)-sparse and has exactly kn − l edges. Thus treesTree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
are exactly the (1,1)-tight graphs, forests are exactly the (1,1)-sparse graphs, and graphs with arboricity
Arboricity
The arboricity of an undirected graph is the minimum number of forests into which its edges can be partitioned. Equivalently it is the minimum number of spanning forests needed to cover all the edges of the graph.-Example:...
k are exactly the (k,k)-sparse graphs. Pseudoforest
Pseudoforest
In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be...
s are exactly the (1,0)-sparse graphs, and the Laman graph
Laman graph
In graph theory, the Laman graphs are a family of sparse graphs describing the minimally rigid systems of rods and joints in the plane. Formally, a Laman graph is a graph on n vertices such that, for all k, every k-vertex subgraph has at most 2k −3 edges, and such that the whole graph...
s arising in rigidity theory are exactly the (2,3)-tight graphs.
Other graph families not characterized by their sparsity can also be described in this way. For instance the facts that any planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
with n vertices has at most 3n - 6 edges, and that any subgraph of a planar graph is planar, together imply that the planar graphs are (3,6)-sparse. However, not every (3,6)-sparse graph is planar. Similarly, outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
s are (2,3)-sparse and planar bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
s are (2,4)-sparse.
Streinu and Theran show that testing (k,l)-sparsity may be performed in polynomial time.

