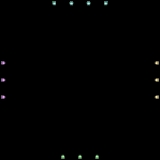
Turán graph
Encyclopedia
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have 
subsets of size 
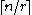, and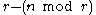 
subsets of size 
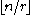. That is, it is a complete r-partite graph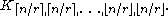
Each vertex has degree eithe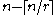r
or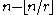 
. The number of edges is
It is a regular graph
, if n is divisible by r.
, who used them to prove Turán's theorem
, an important result in extremal graph theory
.
By the pigeonhole principle, any set of r+1 vertices in the Turán graph includes two vertices in the same partition subset; therefore,
the Turán graph does not contain a clique
of size r+1. According to Turán's theorem, the Turán graph has the maximum possible number of edges among all (r+1)-clique-free graphs with n vertices. Keevash and Sudakov (2003) show that the Turán graph is also the only (r+1)-clique-free graph of order n in which every subset of αn vertices spans at least
edges, if α is sufficiently close to 1. The Erdős–Stone theorem
extends Turán's theorem by bounding the number of edges in a graph that does not have a fixed Turán graph as a subgraph. Via this theorem, similar bounds in extremal graph theory can be proven for any excluded subgraph, depending on the chromatic number of the subgraph.
Several choices of the parameter r in a Turán graph lead to notable graphs that have been independently studied.
The Turán graph T(2n,n) can be formed by removing a perfect matching from a complete graph
K2n. As showed, this graph has boxicity
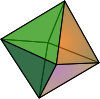
exactly n; it is sometimes known as the Roberts graph. This graph is also the 1-skeleton of an n-dimensional cross-polytope
; for instance, the graph T(6,3) = K2,2,2 is the octahedral graph, the graph of the regular octahedron
. If n couples go to a party, and each person shakes hands with every person except his or her partner, then this graph describes the set of handshakes that take place; for this reason it is also called the cocktail party graph.
The Turán graph T(n,2) is a complete bipartite graph
and, when n is even, a Moore graph. When r is a divisor of n, the Turán graph is symmetric
and strongly regular
, although some authors consider Turán graphs to be a trivial case of strong regularity and therefore exclude them from the definition of a strongly regular graph.
The Turán graph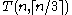
has 3a2b maximal cliques, where
3a+2b=n and b≤2; each maximal clique is formed by choosing one vertex from each partition subset. This is the largest number of maximal cliques possible among all n-vertex graphs regardless of the number of edges in the graph (Moon and Moser 1965); these graphs are sometimes called Moon-Moser graphs.
; that is, it can be formed from individual vertices by a sequence of disjoint union
and complement operations. Specifically, such a sequence can begin by forming each of the independent sets of the Turán graph as a disjoint union of isolated vertices. Then, the overall graph is the complement of the disjoint union of the complements of these independent sets.
Chao and Novacky (1982) show that the Turán graphs are chromatically unique: no other graphs have the same chromatic polynomial
s. Nikiforov (2005) uses Turán graphs to supply a lower bound for the sum of the kth eigenvalues of a graph and its complement.
Falls, Powell, and Snoeyink develop an efficient algorithm for finding clusters of orthologous groups of genes in genome data, by representing the data as a graph and searching for large Turán subgraphs.
Turán graphs also have some interesting properties related to geometric graph theory
. Pór and Wood (2005) give a lower bound of Ω((rn)3/4) on the volume of any three-dimensional grid embedding
of the Turán graph. Witsenhausen (1974) conjectures that the maximum sum of squared distances, among n points with unit diameter in Rd, is attained for a configuration formed by embedding a Turán graph onto the vertices of a regular simplex.
An n-vertex graph G is a subgraph of a Turán graph T(n,r) if and only if G admits an equitable coloring
with r colors. The partition of the Turán graph into independent sets corresponds to the partition of G into color classes. In particular, the Turán graph is the unique maximal n-vertex graph with an r-color equitable coloring.
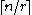subsets of size , and 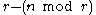subsets of size 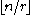. That is, it is a complete r-partite graph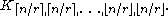Each vertex has degree either
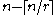or 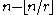. The number of edges isIt is a regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
, if n is divisible by r.
Turán's theorem
Turán graphs are named after Pál TuránPál Turán
Paul Turán was a Hungarian mathematician who worked primarily in number theory. He had a long collaboration with fellow Hungarian mathematician Paul Erdős, lasting 46 years and resulting in 28 joint papers.- Life and education :...
, who used them to prove Turán's theorem
Turán's theorem
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
, an important result in extremal graph theory
Extremal graph theory
Extremal graph theory is a branch of the mathematical field of graph theory. Extremal graph theory studies extremal graphs which satisfy a certain property. Extremality can be taken with respect to different graph invariants, such as order, size or girth...
.
By the pigeonhole principle, any set of r+1 vertices in the Turán graph includes two vertices in the same partition subset; therefore,
the Turán graph does not contain a clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
of size r+1. According to Turán's theorem, the Turán graph has the maximum possible number of edges among all (r+1)-clique-free graphs with n vertices. Keevash and Sudakov (2003) show that the Turán graph is also the only (r+1)-clique-free graph of order n in which every subset of αn vertices spans at least
edges, if α is sufficiently close to 1. The Erdős–Stone theoremErdos–Stone theorem
In extremal graph theory, the Erdős–Stone theorem is an asymptotic result generalising Turán's theorem to bound the number of edges in an H-free graph for a non-complete graph H...
extends Turán's theorem by bounding the number of edges in a graph that does not have a fixed Turán graph as a subgraph. Via this theorem, similar bounds in extremal graph theory can be proven for any excluded subgraph, depending on the chromatic number of the subgraph.
Special cases
The Turán graph T(2n,n) can be formed by removing a perfect matching from a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K2n. As showed, this graph has boxicity
Boxicity
In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.The boxicity of a graph is the minimum dimension in which a given graph can be represented as an intersection graph of axis-parallel boxes...
exactly n; it is sometimes known as the Roberts graph. This graph is also the 1-skeleton of an n-dimensional cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
; for instance, the graph T(6,3) = K2,2,2 is the octahedral graph, the graph of the regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. If n couples go to a party, and each person shakes hands with every person except his or her partner, then this graph describes the set of handshakes that take place; for this reason it is also called the cocktail party graph.
The Turán graph T(n,2) is a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
and, when n is even, a Moore graph. When r is a divisor of n, the Turán graph is symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
and strongly regular
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
, although some authors consider Turán graphs to be a trivial case of strong regularity and therefore exclude them from the definition of a strongly regular graph.
The Turán graph
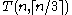has 3a2b maximal cliques, where3a+2b=n and b≤2; each maximal clique is formed by choosing one vertex from each partition subset. This is the largest number of maximal cliques possible among all n-vertex graphs regardless of the number of edges in the graph (Moon and Moser 1965); these graphs are sometimes called Moon-Moser graphs.
Other properties
Every Turán graph is a cographCograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...
; that is, it can be formed from individual vertices by a sequence of disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
and complement operations. Specifically, such a sequence can begin by forming each of the independent sets of the Turán graph as a disjoint union of isolated vertices. Then, the overall graph is the complement of the disjoint union of the complements of these independent sets.
Chao and Novacky (1982) show that the Turán graphs are chromatically unique: no other graphs have the same chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
s. Nikiforov (2005) uses Turán graphs to supply a lower bound for the sum of the kth eigenvalues of a graph and its complement.
Falls, Powell, and Snoeyink develop an efficient algorithm for finding clusters of orthologous groups of genes in genome data, by representing the data as a graph and searching for large Turán subgraphs.
Turán graphs also have some interesting properties related to geometric graph theory
Geometric graph theory
In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs...
. Pór and Wood (2005) give a lower bound of Ω((rn)3/4) on the volume of any three-dimensional grid embedding
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
of the Turán graph. Witsenhausen (1974) conjectures that the maximum sum of squared distances, among n points with unit diameter in Rd, is attained for a configuration formed by embedding a Turán graph onto the vertices of a regular simplex.
An n-vertex graph G is a subgraph of a Turán graph T(n,r) if and only if G admits an equitable coloring
Equitable coloring
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that*No two adjacent vertices have the same color, and...
with r colors. The partition of the Turán graph into independent sets corresponds to the partition of G into color classes. In particular, the Turán graph is the unique maximal n-vertex graph with an r-color equitable coloring.