Negative and non-negative numbers
Encyclopedia
A negative number is any real number
that is less than zero
. Such numbers are often used to represent the amount of a loss or absence. For example, a debt
that is owed may be thought of as a negative asset
, or a decrease in some quantity may be thought of as a negative increase. Negative numbers are also used to describe values on a scale that goes below zero, such as the Celsius
and Fahrenheit
scales for temperature
.
Negative numbers are usually written with a minus sign
in front. For example, −3 represents a negative quantity with a magnitude of three, and is pronounced “minus three”. Conversely, a number that is greater than zero is called positive; zero is usually thought of as neither positive nor negative. The positivity of a number may be emphasized by placing a plus sign before it, e.g. . In general, the negativity or positivity of a number is referred to as its sign
.
In mathematics
, every real number
other than zero is either positive or negative. The positive whole numbers are referred to as natural number
s, while the positive and negative whole numbers (together with zero) are referred to as integer
s.
In bookkeeping
, amounts owed are often represented by red
numbers, or a number in parentheses, as an alternative notation to represent negative numbers.
Negative numbers appeared for the first time in history in the Nine Chapters on the Mathematical Art , which in its present form dates from the period of the Chinese Han Dynasty
(202 BC. – AD 220), but may well contain much older material. India
n mathematicians developed consistent and correct rules on the use of negative numbers, which later spread to the Middle East, and then into Europe. Prior to the concept of negative numbers, negative solutions to problems were considered "false" and equations requiring negative solutions were described as absurd.
of a larger number from a smaller. For example, negative three is the result of subtracting three from zero:
In general, the subtraction of a larger number from a smaller yields a negative result, with the magnitude of the result being the difference between the two numbers. For example,
since .
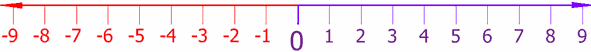Numbers appearing farther to the right on this line are greater, while numbers appearing farther to the left are less. Thus zero appears in the middle, with the positive numbers to the right and the negative numbers to the left.
Note that a negative number with greater magnitude is considered less. For example even though (positive) is greater than (positive) , written
negative is considered to be less than negative :
In addition, any negative number is less than any positive number, so
other than zero is either positive or negative, while zero itself is not considered to have a sign. Positive numbers are sometimes written with a plus sign in front, e.g. denotes a positive three.
Because zero is neither positive nor negative, the term non-negative is sometimes used to refer to a number that is either positive or zero, while non-positive is used to refer to a number that is either negative or zero.
"−" signifies the operator for both the binary (two-operand
) operation
of subtraction
(as in ) and the unary (one-operand
) operation
of negation
(as in , or twice in ). A special case of unary negation occurs when it operates on a positive number, in which case the result is a negative number (as in ).
The ambiguity of the "-" symbol does not generally lead to ambiguity in arithmetic
expressions, because the order of operations makes only one interpretation or the other possible for each "-". However, it can lead to confusion and be difficult for a person to understand an expression when operator symbols appear adjacent to one another. A solution can be to parenthesize the unary "-" along with its operand.
For example, the expression may be clearer if written (even though they mean exactly the same thing formally). The subtraction
expression is a different expression that doesn't represent the same operations, but it evaluates to the same result.
Sometimes in elementary school
s a number may be prefixed by a superscript minus sign or plus sign to explicitly distinguish negative and positive numbers as in
The idea is that two debts can be combined into a single debt of greater magnitude.
When adding together a mixture of positive of negative numbers, one can think of the negative numbers as positive quantities as being subtracted. For example:
In the first example, a credit of is combined with a debt of , which yields a total credit of . If the negative number has greater magnitude, then the result is negative:
Here the credit is less than the debt, so the net result is a debt.
In general, subtraction of a positive number is the same thing as addition of a negative. Thus
and
On the other hand, subtracting a negative number is the same as adding a positive. (The idea is that losing a debt is the same thing as gaining a credit.) Thus
and
of the product is determined by the following rules:
Thus
and
The reason behind the first example is simple: adding three 's together yields :
The reasoning behind the second example is more complicated. The idea again is that losing a debt is the same thing as gaining a credit. In this case, losing two debts of three each is the same as gaining a credit of six:
The convention that a product of two negative numbers is positive is also necessary for multiplication to follow the distributive law. In this case, we know that
Since , the product must equal .
These rules lead to another (equivalent) rule—the sign of any product a × b depends on the sign of a as follows:
are the same as for multiplication. For example,
and
If dividend and divisor have the same sign, the result is always positive.
. For example, is the negation of the positive number . The sum
of a number and its negation is equal to zero:
That is, the negation of a positive number is the additive inverse
of the number.
Using algebra
, we may write this principle as an algebraic identity:
This identity holds for any positive number . It can be made to hold for all real numbers by extending the definition of negation to include zero and negative numbers. Specifically:
For example, the negation of is . In general,
The absolute value
of a number is the non-negative number with the same magnitude. For example, the absolute value of and the absolute value of are both equal to , and the absolute value of is .
s, we can extend the natural number
s N to the integer
s Z by defining integers as an ordered pair
of natural numbers (a, b). We can extend addition and multiplication to these pairs with the following rules: + (c, d) = (a + c, b + d) × (c, d) = (a × c + b × d, a × d + b × c)
We define an equivalence relation
~ upon these pairs with the following rule: ~ (c, d) if and only if a + d = b + c.
This equivalence relation is compatible with the addition and multiplication defined above, and we may define Z to be the quotient set N²/~, i.e. we identify two pairs (a, b) and (c, d) if they are equivalent in the above sense. Note that Z, equipped with these operations of addition and multiplication, is a ring
, and is in fact, the prototypical example of a ring.
We can also define a total order
on Z by writing ≤ (c, d) if and only if a + d ≤ b + c.
This will lead to an additive zero of the form (a, a), an additive inverse
of (a, b) of the form (b, a), a multiplicative unit of the form (a + 1, a), and a definition of subtraction
− (c, d) = (a + d, b + c).
This construction is a special case of the Grothendieck construction.
Let x be a number and let y be its negative.
Suppose y′ is another negative of x. By an axiom
of the real number system
And so, x + y′ = x + y. Using the law of cancellation for addition, it is seen that
y′ = y. Thus y is equal to any other negative of x. That is, y is the unique negative of x.
(202 BC. – AD 220), but may well contain much older material. The Nine Chapters used red counting rods
to denote positive coefficient
s and black rods for negative. (This system is the exact opposite of contemporary printing of positive and negative numbers in the fields of banking, accounting, and commerce
, wherein red numbers denote negative values and black numbers signify positive values). The Chinese were also able to solve simultaneous equations involving negative numbers.
For a long time, negative solutions to problems were considered "false". In Hellenistic Egypt, Diophantus
in the third century A.D. referred to an equation that was equivalent to 4x + 20 = 0 (which has a negative solution) in Arithmetica
, saying that the equation was absurd.
The use of negative numbers was known in early India
, and their role in situations like mathematical problems of debt was understood. Consistent and correct rules for working with these numbers were formulated. The diffusion of this concept led the Arab
intermediaries to pass it to Europe
.
The ancient Indian Bakhshali Manuscript
, which Pearce Ian claimed was written some time between 200 BC. and AD 300, while George Gheverghese Joseph dates it to about AD 400 and no later than the early 7th century, carried out calculations with negative numbers, using "+" as a negative sign.
During the 7th century AD, negative numbers were used in India to represent debts. The Indian mathematician
Brahmagupta
, in Brahma-Sphuta-Siddhanta
(written in A.D. 628), discussed the use of negative numbers to produce the general form quadratic formula that remains in use today. He also found negative solutions of quadratic equation
s and gave rules regarding operations involving negative numbers and zero
, such as "A debt cut off from nothingness becomes a credit; a credit cut off from nothingness becomes a debt. " He called positive numbers "fortunes," zero "a cipher," and negative numbers "debts."
During the 8th century AD, the Islamic world learned about negative numbers from Arabic translations of Brahmagupta's works, and by the 10th century Islamic mathematicians were using negative numbers for debts. The earliest known Islamic text that uses negative numbers is A Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen by Abū al-Wafā' al-Būzjānī.
In the 12th century AD in India, Bhāskara II also gave negative roots for quadratic equations but rejected them because they were inappropriate in the context of the problem. He stated that a negative value is "in this case not to be taken, for it is inadequate; people do not approve of negative roots."
Knowledge of negative numbers eventually reached Europe through Latin
translations of Arabic and Indian works.
European mathematicians, for the most part, resisted the concept of negative numbers until the 17th century, although Fibonacci allowed negative solutions in financial problems where they could be interpreted as debits (chapter 13 of Liber Abaci
, AD 1202) and later as losses (in Flos).
In the 15th century, Nicolas Chuquet
, a Frenchman, used negative numbers as exponents
and referred to them as “absurd numbers.”
In A.D. 1759, Francis Maseres
, an English mathematician, wrote that negative numbers "darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple". He came to the conclusion that negative numbers were nonsensical.
In the 18th century it was common practice to ignore any negative results derived from equations, on the assumption that they were meaningless.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
that is less than zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. Such numbers are often used to represent the amount of a loss or absence. For example, a debt
Debt
A debt is an obligation owed by one party to a second party, the creditor; usually this refers to assets granted by the creditor to the debtor, but the term can also be used metaphorically to cover moral obligations and other interactions not based on economic value.A debt is created when a...
that is owed may be thought of as a negative asset
Asset
In financial accounting, assets are economic resources. Anything tangible or intangible that is capable of being owned or controlled to produce value and that is held to have positive economic value is considered an asset...
, or a decrease in some quantity may be thought of as a negative increase. Negative numbers are also used to describe values on a scale that goes below zero, such as the Celsius
Celsius
Celsius is a scale and unit of measurement for temperature. It is named after the Swedish astronomer Anders Celsius , who developed a similar temperature scale two years before his death...
and Fahrenheit
Fahrenheit
Fahrenheit is the temperature scale proposed in 1724 by, and named after, the German physicist Daniel Gabriel Fahrenheit . Within this scale, the freezing of water into ice is defined at 32 degrees, while the boiling point of water is defined to be 212 degrees...
scales for temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
.
Negative numbers are usually written with a minus sign
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
in front. For example, −3 represents a negative quantity with a magnitude of three, and is pronounced “minus three”. Conversely, a number that is greater than zero is called positive; zero is usually thought of as neither positive nor negative. The positivity of a number may be emphasized by placing a plus sign before it, e.g. . In general, the negativity or positivity of a number is referred to as its sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
.
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, every real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
other than zero is either positive or negative. The positive whole numbers are referred to as natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, while the positive and negative whole numbers (together with zero) are referred to as integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
In bookkeeping
Bookkeeping
Bookkeeping is the recording of financial transactions. Transactions include sales, purchases, income, receipts and payments by an individual or organization. Bookkeeping is usually performed by a bookkeeper. Bookkeeping should not be confused with accounting. The accounting process is usually...
, amounts owed are often represented by red
Red
Red is any of a number of similar colors evoked by light consisting predominantly of the longest wavelengths of light discernible by the human eye, in the wavelength range of roughly 630–740 nm. Longer wavelengths than this are called infrared , and cannot be seen by the naked eye...
numbers, or a number in parentheses, as an alternative notation to represent negative numbers.
Negative numbers appeared for the first time in history in the Nine Chapters on the Mathematical Art , which in its present form dates from the period of the Chinese Han Dynasty
Han Dynasty
The Han Dynasty was the second imperial dynasty of China, preceded by the Qin Dynasty and succeeded by the Three Kingdoms . It was founded by the rebel leader Liu Bang, known posthumously as Emperor Gaozu of Han. It was briefly interrupted by the Xin Dynasty of the former regent Wang Mang...
(202 BC. – AD 220), but may well contain much older material. India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n mathematicians developed consistent and correct rules on the use of negative numbers, which later spread to the Middle East, and then into Europe. Prior to the concept of negative numbers, negative solutions to problems were considered "false" and equations requiring negative solutions were described as absurd.
As the result of subtraction
Negative numbers can be thought of as resulting from the subtractionSubtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
of a larger number from a smaller. For example, negative three is the result of subtracting three from zero:
In general, the subtraction of a larger number from a smaller yields a negative result, with the magnitude of the result being the difference between the two numbers. For example,
since .
The number line
The relationship between negative numbers, positive numbers, and zero is often expressed in the form of a number line: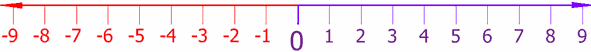Note that a negative number with greater magnitude is considered less. For example even though (positive) is greater than (positive) , written
negative is considered to be less than negative :
In addition, any negative number is less than any positive number, so
- and
Signed numbers
In the context of negative numbers, a number that is greater than zero is referred to as positive. Thus every real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
other than zero is either positive or negative, while zero itself is not considered to have a sign. Positive numbers are sometimes written with a plus sign in front, e.g. denotes a positive three.
Because zero is neither positive nor negative, the term non-negative is sometimes used to refer to a number that is either positive or zero, while non-positive is used to refer to a number that is either negative or zero.
Arithmetic involving negative numbers
The minus signPlus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
"−" signifies the operator for both the binary (two-operand
Operand
In mathematics, an operand is the object of a mathematical operation, a quantity on which an operation is performed.-Example :The following arithmetic expression shows an example of operators and operands:3 + 6 = 9\;...
) operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
of subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
(as in ) and the unary (one-operand
Operand
In mathematics, an operand is the object of a mathematical operation, a quantity on which an operation is performed.-Example :The following arithmetic expression shows an example of operators and operands:3 + 6 = 9\;...
) operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
of negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
(as in , or twice in ). A special case of unary negation occurs when it operates on a positive number, in which case the result is a negative number (as in ).
The ambiguity of the "-" symbol does not generally lead to ambiguity in arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
expressions, because the order of operations makes only one interpretation or the other possible for each "-". However, it can lead to confusion and be difficult for a person to understand an expression when operator symbols appear adjacent to one another. A solution can be to parenthesize the unary "-" along with its operand.
For example, the expression may be clearer if written (even though they mean exactly the same thing formally). The subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
expression is a different expression that doesn't represent the same operations, but it evaluates to the same result.
Sometimes in elementary school
Elementary school
An elementary school or primary school is an institution where children receive the first stage of compulsory education known as elementary or primary education. Elementary school is the preferred term in some countries, particularly those in North America, where the terms grade school and grammar...
s a number may be prefixed by a superscript minus sign or plus sign to explicitly distinguish negative and positive numbers as in
- gives .
Addition
Addition of two negative numbers is very similar to addition of two positive numbers. For example,- .
The idea is that two debts can be combined into a single debt of greater magnitude.
When adding together a mixture of positive of negative numbers, one can think of the negative numbers as positive quantities as being subtracted. For example:
- and .
In the first example, a credit of is combined with a debt of , which yields a total credit of . If the negative number has greater magnitude, then the result is negative:
- and .
Here the credit is less than the debt, so the net result is a debt.
Subtraction
As discussed above, it is possible for the subtraction of two non-negative numbers to yield a negative answer:In general, subtraction of a positive number is the same thing as addition of a negative. Thus
and
On the other hand, subtracting a negative number is the same as adding a positive. (The idea is that losing a debt is the same thing as gaining a credit.) Thus
and
- .
Multiplication
When multiplying numbers, the magnitude of the product is always just the product of the two magnitudes. The signSign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
of the product is determined by the following rules:
- The product of one positive number and one negative number is negative.
- The product of two negative numbers is positive.
Thus
and
- .
The reason behind the first example is simple: adding three 's together yields :
- .
The reasoning behind the second example is more complicated. The idea again is that losing a debt is the same thing as gaining a credit. In this case, losing two debts of three each is the same as gaining a credit of six:
- debts each credit.
The convention that a product of two negative numbers is positive is also necessary for multiplication to follow the distributive law. In this case, we know that
- .
Since , the product must equal .
These rules lead to another (equivalent) rule—the sign of any product a × b depends on the sign of a as follows:
- if a is positive, then the sign of a × b is the same as the sign of b, and
- if a is negative, then the sign of a × b is the opposite of the sign of b.
Division
The sign rules for divisionDivision (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
are the same as for multiplication. For example,
- ,
- ,
and
- .
If dividend and divisor have the same sign, the result is always positive.
Negation
The negative version of a positive number is referred to as its negationNegation (algebra)
Negation is the mathematical operation that reverses the sign of a number. Thus the negation of a positive number is negative, and the negation of a negative number is positive. The negation of zero is zero...
. For example, is the negation of the positive number . The sum
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
of a number and its negation is equal to zero:
- .
That is, the negation of a positive number is the additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of the number.
Using algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, we may write this principle as an algebraic identity:
- .
This identity holds for any positive number . It can be made to hold for all real numbers by extending the definition of negation to include zero and negative numbers. Specifically:
- The negation of 0 is 0, and
- The negation of a negative number is the corresponding positive number.
For example, the negation of is . In general,
- .
The absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of a number is the non-negative number with the same magnitude. For example, the absolute value of and the absolute value of are both equal to , and the absolute value of is .
Formal construction of negative integers
In a similar manner to rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, we can extend the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s N to the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z by defining integers as an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
of natural numbers (a, b). We can extend addition and multiplication to these pairs with the following rules: + (c, d) = (a + c, b + d) × (c, d) = (a × c + b × d, a × d + b × c)
We define an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
~ upon these pairs with the following rule: ~ (c, d) if and only if a + d = b + c.
This equivalence relation is compatible with the addition and multiplication defined above, and we may define Z to be the quotient set N²/~, i.e. we identify two pairs (a, b) and (c, d) if they are equivalent in the above sense. Note that Z, equipped with these operations of addition and multiplication, is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, and is in fact, the prototypical example of a ring.
We can also define a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
on Z by writing ≤ (c, d) if and only if a + d ≤ b + c.
This will lead to an additive zero of the form (a, a), an additive inverse
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of (a, b) of the form (b, a), a multiplicative unit of the form (a + 1, a), and a definition of subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
− (c, d) = (a + d, b + c).
This construction is a special case of the Grothendieck construction.
Uniqueness
The negative of a number is unique, as is shown by the following proof.Let x be a number and let y be its negative.
Suppose y′ is another negative of x. By an axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
of the real number system
And so, x + y′ = x + y. Using the law of cancellation for addition, it is seen that
y′ = y. Thus y is equal to any other negative of x. That is, y is the unique negative of x.
History
Negative numbers appear for the first time in history in the Nine Chapters on the Mathematical Art (Jiu zhang suan-shu), which in its present form dates from the period of the Han DynastyHan Dynasty
The Han Dynasty was the second imperial dynasty of China, preceded by the Qin Dynasty and succeeded by the Three Kingdoms . It was founded by the rebel leader Liu Bang, known posthumously as Emperor Gaozu of Han. It was briefly interrupted by the Xin Dynasty of the former regent Wang Mang...
(202 BC. – AD 220), but may well contain much older material. The Nine Chapters used red counting rods
Counting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
to denote positive coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s and black rods for negative. (This system is the exact opposite of contemporary printing of positive and negative numbers in the fields of banking, accounting, and commerce
Commerce
While business refers to the value-creating activities of an organization for profit, commerce means the whole system of an economy that constitutes an environment for business. The system includes legal, economic, political, social, cultural, and technological systems that are in operation in any...
, wherein red numbers denote negative values and black numbers signify positive values). The Chinese were also able to solve simultaneous equations involving negative numbers.
For a long time, negative solutions to problems were considered "false". In Hellenistic Egypt, Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
in the third century A.D. referred to an equation that was equivalent to 4x + 20 = 0 (which has a negative solution) in Arithmetica
Arithmetica
Arithmetica is an ancient Greek text on mathematics written by the mathematician Diophantus in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate equations and indeterminate equations.Equations in the book are called Diophantine equations...
, saying that the equation was absurd.
The use of negative numbers was known in early India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
, and their role in situations like mathematical problems of debt was understood. Consistent and correct rules for working with these numbers were formulated. The diffusion of this concept led the Arab
Arab
Arab people, also known as Arabs , are a panethnicity primarily living in the Arab world, which is located in Western Asia and North Africa. They are identified as such on one or more of genealogical, linguistic, or cultural grounds, with tribal affiliations, and intra-tribal relationships playing...
intermediaries to pass it to Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
.
The ancient Indian Bakhshali Manuscript
Bakhshali Manuscript
The Bakhshali Manuscript is an Ancient Indian mathematical manuscript written on birch bark which was found near the village of Bakhshali in 1881 in what was then the North-West Frontier Province of British India...
, which Pearce Ian claimed was written some time between 200 BC. and AD 300, while George Gheverghese Joseph dates it to about AD 400 and no later than the early 7th century, carried out calculations with negative numbers, using "+" as a negative sign.
During the 7th century AD, negative numbers were used in India to represent debts. The Indian mathematician
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
, in Brahma-Sphuta-Siddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
(written in A.D. 628), discussed the use of negative numbers to produce the general form quadratic formula that remains in use today. He also found negative solutions of quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s and gave rules regarding operations involving negative numbers and zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, such as "A debt cut off from nothingness becomes a credit; a credit cut off from nothingness becomes a debt. " He called positive numbers "fortunes," zero "a cipher," and negative numbers "debts."
During the 8th century AD, the Islamic world learned about negative numbers from Arabic translations of Brahmagupta's works, and by the 10th century Islamic mathematicians were using negative numbers for debts. The earliest known Islamic text that uses negative numbers is A Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen by Abū al-Wafā' al-Būzjānī.
In the 12th century AD in India, Bhāskara II also gave negative roots for quadratic equations but rejected them because they were inappropriate in the context of the problem. He stated that a negative value is "in this case not to be taken, for it is inadequate; people do not approve of negative roots."
Knowledge of negative numbers eventually reached Europe through Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
translations of Arabic and Indian works.
European mathematicians, for the most part, resisted the concept of negative numbers until the 17th century, although Fibonacci allowed negative solutions in financial problems where they could be interpreted as debits (chapter 13 of Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
, AD 1202) and later as losses (in Flos).
In the 15th century, Nicolas Chuquet
Nicolas Chuquet
Nicolas Chuquet was a French mathematician whose great work, Triparty en la science des nombres , was unpublished in his lifetime...
, a Frenchman, used negative numbers as exponents
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
and referred to them as “absurd numbers.”
In A.D. 1759, Francis Maseres
Francis Maseres
Francis Maseres was an English lawyer. He is known as attorney general of the Province of Quebec, judge, mathematician, historian, member of the Royal Society, and cursitor baron of the exchequer.- Biography :...
, an English mathematician, wrote that negative numbers "darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple". He came to the conclusion that negative numbers were nonsensical.
In the 18th century it was common practice to ignore any negative results derived from equations, on the assumption that they were meaningless.