
Second derivative
Encyclopedia
In calculus
, the second derivative of a function
ƒ is the derivative
of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is the instantaneous acceleration
of the vehicle, or the rate at which the velocity
of the vehicle is changing.
On the graph of a function
, the second derivative corresponds to the curvature
or concavity of the graph. The graph of a function with positive second derivative curves upwards, while the graph of a function with negative second derivative curves downwards.
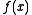 is usually denoted
is usually denoted 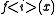 . That is:
. That is: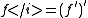
When using Leibniz's notation for derivatives, the second derivative of a dependent variable y with respect to an independent variable x is written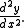
This notation is derived from the following formula: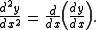

the derivative of ƒ is the function
The second derivative of ƒ is the derivative of ƒ′, namely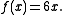

line will lie below the graph of the function. Similarly, a function whose second derivative is negative will be concave down (sometimes called simply “concave”), and its tangent lines will lie above the graph of the function.
for a function (i.e. a point where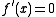 ) is a local maximum or a local minimum. Specifically,
) is a local maximum or a local minimum. Specifically,
The reason the second derivative produces these results can be seen by way of a real-world analogy. Consider a vehicle that at first is moving forward at a great velocity, but with a negative acceleration. Clearly the position of the vehicle at the point where the velocity reaches zero will be the maximum distance from the starting position – after this time, the velocity will become negative and the vehicle will reverse. The same is true for the minimum, with a vehicle that at first has a very negative velocity but positive acceleration.
for the second derivative: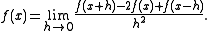
The expression on the right can be written as a difference quotient
of difference quotients:
This limit can be viewed as a continuous version of the second difference for sequences.
s, the second derivative is related to the best quadratic approximation for a function ƒ. This is the quadratic function
whose first and second derivatives are the same as those of ƒ at a given point. The formula for the best quadratic approximation to a function ƒ around the point x = a is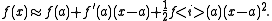
This quadratic approximation is the second-order Taylor polynomial for the function centered at x = a.
can be obtained. For example, assuming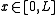 and homogeneous Dirichlet boundary conditions, i.e.,
and homogeneous Dirichlet boundary conditions, i.e., 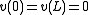 , the eigenvalues are
, the eigenvalues are  and the corresponding eigenvectors (also called eigenfunctions) are
and the corresponding eigenvectors (also called eigenfunctions) are 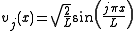 . Here,
. Here, 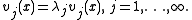
For other well-known cases, see the main article eigenvalues and eigenvectors of the second derivative
.
s. For a function ƒ:R3 → R, these include the three second-order partials

and the mixed partials
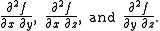
If the function's image and domain both have a potential, then these fit together into a symmetric matrix known as the Hessian. The eigenvalues of this matrix can be used to implement a multivariable analogue of the second derivative test. (See also the second partial derivative test
.)
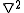 defined by
defined by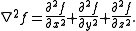
The Laplacian of a function is equal to the divergence
of the gradient
.
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the second derivative of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
ƒ is the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is the instantaneous acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of the vehicle, or the rate at which the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the vehicle is changing.
On the graph of a function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
, the second derivative corresponds to the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
or concavity of the graph. The graph of a function with positive second derivative curves upwards, while the graph of a function with negative second derivative curves downwards.
Notation
The second derivative of a function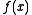 is usually denoted
is usually denoted 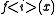 . That is:
. That is: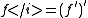
When using Leibniz's notation for derivatives, the second derivative of a dependent variable y with respect to an independent variable x is written
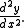
This notation is derived from the following formula:
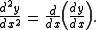
Example
Given the function
the derivative of ƒ is the function

The second derivative of ƒ is the derivative of ƒ′, namely
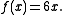
Relation to the graph

Concavity
The second derivative of a function ƒ measures the concavity of the graph of ƒ. A function whose second derivative is positive will be concave up (sometimes referred to as convex), meaning that the tangentTangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
line will lie below the graph of the function. Similarly, a function whose second derivative is negative will be concave down (sometimes called simply “concave”), and its tangent lines will lie above the graph of the function.
Inflection points
If the second derivative of a function changes sign, the graph of the function will switch from concave down to concave up, or vice versa. A point where this occurs is called an inflection point. Assuming the second derivative is continuous, it must take a value of zero at any inflection point, although not every point where the second derivative is zero is necessarily a point of inflection.Second derivative test
The relation between the second derivative and the graph can be used to test whether a stationary pointStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
for a function (i.e. a point where
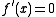 ) is a local maximum or a local minimum. Specifically,
) is a local maximum or a local minimum. Specifically,
- If
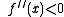 then
then 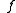 has a local maximum at
has a local maximum at 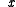 .
. - If
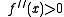 then
then  has a local minimum at
has a local minimum at 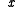 .
. - If
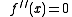 , the second derivative test says nothing about the point
, the second derivative test says nothing about the point 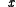 , a possible inflection point.
, a possible inflection point.
The reason the second derivative produces these results can be seen by way of a real-world analogy. Consider a vehicle that at first is moving forward at a great velocity, but with a negative acceleration. Clearly the position of the vehicle at the point where the velocity reaches zero will be the maximum distance from the starting position – after this time, the velocity will become negative and the vehicle will reverse. The same is true for the minimum, with a vehicle that at first has a very negative velocity but positive acceleration.
Limit
It is possible to write a single limitLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
for the second derivative:
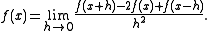
The expression on the right can be written as a difference quotient
Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
of difference quotients:

This limit can be viewed as a continuous version of the second difference for sequences.
Quadratic approximation
Just as the first derivative is related to linear approximationLinear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
s, the second derivative is related to the best quadratic approximation for a function ƒ. This is the quadratic function
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
whose first and second derivatives are the same as those of ƒ at a given point. The formula for the best quadratic approximation to a function ƒ around the point x = a is
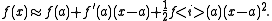
This quadratic approximation is the second-order Taylor polynomial for the function centered at x = a.
Eigenvalues and eigenvectors of the second derivative
For many combinations of boundary conditions explicit formulas for eigenvalues and eigenvectors of the second derivativeEigenvalues and eigenvectors of the second derivative
Explicit formulas for eigenvalues and eigenvectors of the second derivative with different boundary conditions are provided both for the continuous and discrete cases...
can be obtained. For example, assuming
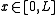 and homogeneous Dirichlet boundary conditions, i.e.,
and homogeneous Dirichlet boundary conditions, i.e., 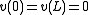 , the eigenvalues are
, the eigenvalues are  and the corresponding eigenvectors (also called eigenfunctions) are
and the corresponding eigenvectors (also called eigenfunctions) are 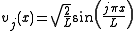 . Here,
. Here, 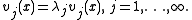
For other well-known cases, see the main article eigenvalues and eigenvectors of the second derivative
Eigenvalues and eigenvectors of the second derivative
Explicit formulas for eigenvalues and eigenvectors of the second derivative with different boundary conditions are provided both for the continuous and discrete cases...
.
The Hessian
The second derivative generalizes to higher dimensions through the notion of second partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s. For a function ƒ:R3 → R, these include the three second-order partials

and the mixed partials
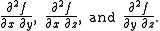
If the function's image and domain both have a potential, then these fit together into a symmetric matrix known as the Hessian. The eigenvalues of this matrix can be used to implement a multivariable analogue of the second derivative test. (See also the second partial derivative test
Second partial derivative test
In mathematics, the second partial derivative test is a method in multivariable calculus used to determine if a critical point of a function f is a minimum, maximum or saddle point.-Explanation:Suppose that...
.)
The Laplacian
Another common generalization of the second derivative is the Laplacian. This is the differential operator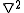 defined by
defined by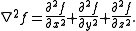
The Laplacian of a function is equal to the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
.

