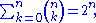Double counting (proof technique)
Encyclopedia
In combinatorics
, double counting, also called counting in two ways, is a combinatorial proof
technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set. In this technique, which call “one of the most important tools in combinatorics,” one describes a finite set X from two perspectives leading to two distinct expressions for the size of the set. Since both expressions equal the size of the same set, they equal each other.
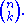
Therefore the total number of possible committees is the sum of binomial coefficients over k = 0, 1, 2, ... n. Equating the two expressions gives the identity
a special case of the binomial theorem
. The committees counted in this way may also be interpreted as the vertices
of a hypercube
; a similar double counting method for higher dimensional hypercube features can be used to prove the more general identity
.
. That is, the number of vertices that have an odd number of incident edges must be even. In more colloquial terms, in a party of people some of whom shake hands, an even number of people must have shaken an odd number of other people's hands; for this reason, the result is known as the handshaking lemma
.
To prove this by double counting, let d(v) be the degree of vertex v. The number of vertex-edge incidences in the graph may be counted in two different ways: by summing the degrees of the vertices, or by counting two incidences for every edge. Therefore
where e is the number of edges. The sum of the degrees of the vertices is therefore an even number, which could not happen if an odd number of the vertices had odd degree. This fact, with this proof, appears in the 1736 paper of Leonhard Euler
on the Seven Bridges of Königsberg
that first began the study of graph theory
.
 What is the number Tn of different trees
What is the number Tn of different trees
that can be formed from a set of n distinct vertices? Cayley's formula gives the answer . list four proofs of this fact; they write of the fourth, a double counting proof due to Jim Pitman, that it is “the most beautiful of them all.”
Pitman's proof counts in two different ways the number of different sequences of directed edges that can be added to an empty graph on n vertices to form from it a rooted tree. One way to form such a sequence is to start with one of the Tn possible unrooted trees, choose one of its n vertices as root, and choose one of the possible sequences in which to add its edges. Therefore, the total number of sequences that can be formed in this way is .
Another way to count these edge sequences is to consider adding the edges one by one to an empty graph, and to count the number of choices available at each step. If one has added a collection of edges already, so that the graph formed by these edges is a rooted forest with k trees, there are choices for the next edge to add: its starting vertex can be any one of the n vertices of the graph, and its ending vertex can be any one of the k roots other than the root of the tree containing the starting vertex. Therefore, if one multiplies together the number of choices from the first step, the second step, etc., the total number of choices is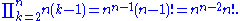
Equating these two formulas for the number of edge sequences results in Cayley's formula:
and
As Aigner and Ziegler describe, the formula and the proof can be generalized to count the number of rooted forests with k trees, for any k.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, double counting, also called counting in two ways, is a combinatorial proof
Combinatorial proof
In mathematics, the term combinatorial proof is often used to mean either of two types of proof of an identity in enumerative combinatorics that either states that two sets of combinatorial configurations, depending on one or more parameters, have the same number of elements , or gives a formula...
technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set. In this technique, which call “one of the most important tools in combinatorics,” one describes a finite set X from two perspectives leading to two distinct expressions for the size of the set. Since both expressions equal the size of the same set, they equal each other.
Forming committees
One example of the double counting method counts the number of ways in which a committee can be formed from n people, allowing any number of the people (even zero of them) to be part of the committee. That is, one counts the number of subsets that an n-element set may have. One method for forming a committee is to ask each person to choose whether or not to join it. Each person has two choices – yes or no – and these choices are independent of those of the other people. Therefore there are 2 × 2 × ... × 2 = 2n possibilities. Alternatively, one may observe that the size of the committee must be some number between 0 and n. For each possible size k, the number of ways in which a committee of k people can be formed from n people is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
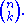
Therefore the total number of possible committees is the sum of binomial coefficients over k = 0, 1, 2, ... n. Equating the two expressions gives the identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
a special case of the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. The committees counted in this way may also be interpreted as the vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
; a similar double counting method for higher dimensional hypercube features can be used to prove the more general identity

.
Handshaking lemma
Another theorem that is commonly proved with a double counting argument states that every undirected graph contains an even number of vertices of odd degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
. That is, the number of vertices that have an odd number of incident edges must be even. In more colloquial terms, in a party of people some of whom shake hands, an even number of people must have shaken an odd number of other people's hands; for this reason, the result is known as the handshaking lemma
Handshaking lemma
In graph theory, a branch of mathematics, the handshaking lemma is the statement that every finite undirected graph has an even number of vertices with odd degree...
.
To prove this by double counting, let d(v) be the degree of vertex v. The number of vertex-edge incidences in the graph may be counted in two different ways: by summing the degrees of the vertices, or by counting two incidences for every edge. Therefore
where e is the number of edges. The sum of the degrees of the vertices is therefore an even number, which could not happen if an odd number of the vertices had odd degree. This fact, with this proof, appears in the 1736 paper of Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
on the Seven Bridges of Königsberg
Seven Bridges of Königsberg
The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and prefigured the idea of topology....
that first began the study of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
Counting trees

Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
that can be formed from a set of n distinct vertices? Cayley's formula gives the answer . list four proofs of this fact; they write of the fourth, a double counting proof due to Jim Pitman, that it is “the most beautiful of them all.”
Pitman's proof counts in two different ways the number of different sequences of directed edges that can be added to an empty graph on n vertices to form from it a rooted tree. One way to form such a sequence is to start with one of the Tn possible unrooted trees, choose one of its n vertices as root, and choose one of the possible sequences in which to add its edges. Therefore, the total number of sequences that can be formed in this way is .
Another way to count these edge sequences is to consider adding the edges one by one to an empty graph, and to count the number of choices available at each step. If one has added a collection of edges already, so that the graph formed by these edges is a rooted forest with k trees, there are choices for the next edge to add: its starting vertex can be any one of the n vertices of the graph, and its ending vertex can be any one of the k roots other than the root of the tree containing the starting vertex. Therefore, if one multiplies together the number of choices from the first step, the second step, etc., the total number of choices is
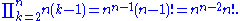
Equating these two formulas for the number of edge sequences results in Cayley's formula:

and

As Aigner and Ziegler describe, the formula and the proof can be generalized to count the number of rooted forests with k trees, for any k.
Additional examples
- Vandermonde's identity, another identity on sums of binomial coefficients that can be proven by double counting.
- Square pyramidal numberSquare pyramidal numberIn mathematics, a pyramid number, or square pyramidal number, is a figurate number that represents the number of stacked spheres in a pyramid with a square base...
. The equality between the sum of the first n square numbers and a cubic polynomial can be shown by double counting the triples of numbers x, y, and z where z is larger than either of the other two numbers. - Lubell–Yamamoto–Meshalkin inequality. Lubell's proof of this result on set families is a double counting argument on permutations, used to prove an inequality rather than an equality.
- Proofs of Fermat's little theoremProofs of Fermat's little theoremThis article collects together a variety of proofs of Fermat's little theorem, which states thata^p \equiv a \pmod p \,\!for every prime number p and every integer a .-Simplifications:...
. A divisibility proof by double counting: for any prime p and natural number A, there are length-p words over an A-symbol alphabet having two or more distinct symbols. These may be grouped into sets of p words that can be transformed into each other by circular shiftCircular shiftIn combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation...
s; these sets are called necklacesNecklace (combinatorics)In combinatorics, a k-ary necklace of length n is an equivalence class of n-character strings over an alphabet of size k, taking all rotations as equivalent...
. Therefore, of necklaces) and is divisible by p. - Proofs of quadratic reciprocityProofs of quadratic reciprocityIn number theory, the law of quadratic reciprocity, like the Pythagorean theorem, has lent itself to an unusual number of proofs. Several hundred proofs of the law of quadratic reciprocity have been found.-Proofs that are accessible:...
. A proof by Eisenstein derives another important number-theoreticNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
fact by double counting lattice points in a triangle.
Related topics
- Bijective proofBijective proofIn combinatorics, bijective proof is a proof technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of...
. Where double counting involves counting one set in two ways, bijective proofs involve counting two sets in one way, by showing that their elements correspond one-for-one. - The inclusion-exclusion principleInclusion-exclusion principleIn combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
, a formula for the size of a union of sets that may, together with another formula for the same union, be used as part of a double counting argument.