
Experimental mathematics
Encyclopedia
Experimental mathematics is an approach to mathematics in which numerical computation is used to investigate mathematical objects and identify properties and patterns. It has been defined as "that branch of mathematics that concerns itself ultimately with the codification and transmission of insights within the mathematical community through the use of experimental (in either the Galilean, Baconian, Aristotelian or Kantian sense) exploration of conjectures and more informal beliefs and a careful analysis of the data acquired in this pursuit."
, typically consist of lists of numerical examples illustrating algebraic identities. However, modern mathematics, beginning in the 17th century, developed a tradition of publishing results in a final, formal and abstract presentation. The numerical examples that may have led a mathematician to originally formulate a general theorem were not published, and were generally forgotten.
Experimental mathematics as a separate area of study re-emerged in the twentieth century, when the invention of the electronic computer vastly increased the range of feasible calculations, with a speed and precision far greater than anything available to previous generations of mathematicians. A significant milestone and achievement of experimental mathematics was the discovery in 1995 of the Bailey–Borwein–Plouffe formula
for the binary digits of π. This formula was discovered not by formal reasoning, but instead
by numerical searches on a computer; only afterwards was a rigorous proof found.
The uses of experimental mathematics have been defined as follows:
s are then used to search for relations between these values and mathematical constants. Working with high precision values reduces the possibility of mistaking a mathematical coincidence for a true relation. A formal proof of a conjectured relation will then be sought – it is often easier to find a formal proof once the form of a conjectured relation is known.
If a counterexample is being sought or a large-scale proof by exhaustion is being attempted, distributed computing
techniques may be used to divide the calculations between multiple computers.
Frequent use is made of general computer algebra system
s such as Mathematica
, although domain-specific software is also written for attacks on problems that require high efficiency. Experimental mathematics software usually includes error detection and correction
mechanisms, integrity checks and redundant calculations designed to minimise the possibility of results being invalidated by a hardware or software error.
History
Mathematicians have always practised experimental mathematics. Existing records of early mathematics, such as Babylonian mathematicsBabylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
, typically consist of lists of numerical examples illustrating algebraic identities. However, modern mathematics, beginning in the 17th century, developed a tradition of publishing results in a final, formal and abstract presentation. The numerical examples that may have led a mathematician to originally formulate a general theorem were not published, and were generally forgotten.
Experimental mathematics as a separate area of study re-emerged in the twentieth century, when the invention of the electronic computer vastly increased the range of feasible calculations, with a speed and precision far greater than anything available to previous generations of mathematicians. A significant milestone and achievement of experimental mathematics was the discovery in 1995 of the Bailey–Borwein–Plouffe formula
Bailey–Borwein–Plouffe formula
The Bailey–Borwein–Plouffe formula provides a spigot algorithm for the computation of the nth binary digit of π. This summation formula was discovered in 1995 by Simon Plouffe. The formula is named after the authors of the paper in which the formula was published, David H. Bailey, Peter Borwein,...
for the binary digits of π. This formula was discovered not by formal reasoning, but instead
by numerical searches on a computer; only afterwards was a rigorous proof found.
Objectives and uses
The objectives of experimental mathematics are "to generate understanding and insight; to generate and confirm or confront conjectures; and generally to make mathematics more tangible, lively and fun for both the professional researcher and the novice".The uses of experimental mathematics have been defined as follows:
- Gaining insight and intuition.
- Discovering new patterns and relationships.
- Using graphical displays to suggest underlying mathematical principles.
- Testing and especially falsifying conjectures.
- Exploring a possible result to see if it is worth formal proof.
- Suggesting approaches for formal proof.
- Replacing lengthy hand derivations with computer-based derivations.
- Confirming analytically derived results.
Tools and techniques
Experimental mathematics makes use of numerical methods to calculate approximate values for integrals and infinite series. Arbitrary precision arithmetic is often used to establish these values to a high degree of precision – typically 100 significant figures or more. Integer relation algorithmInteger relation algorithm
An integer relation between a set of real numbers x1, x2, ..., xn is a set of integers a1, a2, ..., an, not all 0, such thata_1x_1 + a_2x_2 + \cdots + a_nx_n = 0.\,...
s are then used to search for relations between these values and mathematical constants. Working with high precision values reduces the possibility of mistaking a mathematical coincidence for a true relation. A formal proof of a conjectured relation will then be sought – it is often easier to find a formal proof once the form of a conjectured relation is known.
If a counterexample is being sought or a large-scale proof by exhaustion is being attempted, distributed computing
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
techniques may be used to divide the calculations between multiple computers.
Frequent use is made of general computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s such as Mathematica
Mathematica
Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
, although domain-specific software is also written for attacks on problems that require high efficiency. Experimental mathematics software usually includes error detection and correction
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
mechanisms, integrity checks and redundant calculations designed to minimise the possibility of results being invalidated by a hardware or software error.
Applications and examples
Applications and examples of experimental mathematics include:- Searching for a counterexample to a conjecture
- Roger Frye used experimental mathematics techniques to find the smallest counterexample to Euler's sum of powers conjecture.
- The ZetaGridZetaGridZetaGrid was at one time the largest distributed computing project designed to explore roots of the Riemann zeta function, checking over one billion roots a day....
project was set up to search for a counterexample to the Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. - This project is searching for a counterexample to the Collatz conjectureCollatz conjectureThe Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture, the Ulam conjecture , Kakutani's problem , the Thwaites conjecture , Hasse's algorithm The Collatz conjecture is a...
.
- Finding new examples of numbers or objects with particular properties
- The Great Internet Mersenne Prime SearchGreat Internet Mersenne Prime SearchThe Great Internet Mersenne Prime Search is a collaborative project of volunteers who use freely available computer software to search for Mersenne prime numbers. The project was founded by George Woltman, who also wrote the software Prime95 and MPrime for the project...
is searching for new Mersenne primeMersenne primeIn mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
s. - The distributed.netDistributed.netdistributed.net is a worldwide distributed computing effort that is attempting to solve large scale problems using otherwise idle CPU or GPU time. It is officially recognized as a non-profit organization under U.S...
's OGR project is searching for optimal Golomb rulerGolomb rulerIn mathematics, a Golomb ruler is a set of marks at integer positions along an imaginary ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its order, and the largest distance between two of its marks is its length...
s. - The Riesel SieveRiesel SieveRiesel Sieve is a distributed computing project, running in part on the BOINC platform. Its aim is to prove that is the smallest Riesel number, by finding a prime of the form for all odd smaller than .-Progress of the project:...
project is searching for the smallest Riesel numberRiesel numberIn mathematics, a Riesel number is an odd natural number k for which the integers of the form k·2n − 1 are composite for all natural numbers n....
. - The Seventeen or BustSeventeen or BustSeventeen or Bust is a distributed computing project started in March 2002 to solve the last seventeen cases in the Sierpinski problem.-Goals:...
project is searching for the smallest Sierpinski number. - The Sudoku Project is searching for a solution to the minimum Sudoku problem.
- The Great Internet Mersenne Prime Search
- Finding serendipitous numerical patterns
- Edward Lorenz found the Lorenz attractorLorenz attractorThe Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
, an early example of a chaotic dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, by investigating anomalous behaviours in a numerical weather model. - The Ulam spiralUlam spiralThe Ulam spiral, or prime spiral is a simple method of visualizing the prime numbers that reveals the apparent tendency of certain quadratic polynomials to generate unusually large numbers of primes...
was discovered by accident. - Mitchell FeigenbaumMitchell FeigenbaumMitchell Jay Feigenbaum is a mathematical physicist whose pioneering studies in chaos theory led to the discovery of the Feigenbaum constants.- Biography :...
's discovery of the Feigenbaum constant was based initially on numerical observations, followed by a rigorous proof.
- Edward Lorenz found the Lorenz attractor
- Use of computer programs to check a large but finite number of cases to complete a computer-assistedComputer-assisted proofA computer-assisted proof is a mathematical proof that has been at least partially generated by computer.Most computer-aided proofs to date have been implementations of large proofs-by-exhaustion of a mathematical theorem. The idea is to use a computer program to perform lengthy computations, and...
proof by exhaustionProof by exhaustionProof by exhaustion, also known as proof by cases, perfect induction, or the brute force method, is a method of mathematical proof in which the statement to be proved is split into a finite number of cases and each case is checked to see if the proposition in question holds...
- Thomas HalesThomas Callister HalesThomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
's proof of the Kepler conjectureKepler conjectureThe Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
. - Various proofs of the four colour theorem.
- Clement Lam's proof of the non-existence of a finite projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
of order 10.
- Thomas Hales
- Symbolic validation (via Computer algebra) of conjectures to motivate the search for an analytical proof
- Solutions to a special case of the quantum three-body problemThree-body problemThree-body problem has two distinguishable meanings in physics and classical mechanics:# In its traditional sense the three-body problem is the problem of taking an initial set of data that specifies the positions, masses and velocities of three bodies for some particular point in time and then...
known as the hydrogen molecule-ion were found standard quantum chemistry basis sets before realizing they all lead to the same unique analytical solution in terms of a generalization of the Lambert W function. Related to this work is the isolation of a previously unknown link between gravity theory and quantum mechanics in lower dimensions (see quantum gravity and references therein). - In the realm of relativistic many-bodied mechanicsN-body problemThe n-body problem is the problem of predicting the motion of a group of celestial objects that interact with each other gravitationally. Solving this problem has been motivated by the need to understand the motion of the Sun, planets and the visible stars...
, namely the time-symmetricT-symmetryT Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries...
Wheeler–Feynman absorber theory: the equivalence between an advanced Liénard–Wiechert potential of particle j acting on particle i and the corresponding potential for particle i acting on particle j was demonstrated exhaustively to order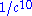 before being proved mathematically.
before being proved mathematically. - In the realm of linear optics, verification of the series expansion of the envelopeSlowly varying envelope approximationIn physics, the slowly varying envelope approximation is the assumption that the envelope of a forward-travelling wave pulse varies slowly in time and space compared to a period or wavelength...
of the electric field for ultrashort light pulses travelling in non isotropic media. Previous expansions had been incomplete: the outcome revealed an extra term vindicated by experiment.
- Solutions to a special case of the quantum three-body problem
- Evaluation of infinite seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, infinite products and integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s (also see symbolic integrationSymbolic integrationIn calculus symbolic integration is the problem of finding a formula for the antiderivative, or indefinite integral, of a given function f, i.e...
), typically by carrying out a high precision numerical calculation, and then using an integer relation algorithmInteger relation algorithmAn integer relation between a set of real numbers x1, x2, ..., xn is a set of integers a1, a2, ..., an, not all 0, such thata_1x_1 + a_2x_2 + \cdots + a_nx_n = 0.\,...
(such as the Inverse Symbolic CalculatorInverse Symbolic CalculatorThe Inverse Symbolic Calculator is an online number checker established July 18, 1995 by Peter Benjamin Borwein, Jonathan Michael Borwein and Simon Plouffe of the Canadian Centre for Experimental and Constructive Mathematics...
) to find a linear combination of mathematical constants that matches this value. For example, the following identity was first conjectured by Enrico Au-Yeung, a student of Jonathan BorweinJonathan BorweinJonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...
using computer search and PSLQ algorithm in 1993:
-

- Visual investigations
- In Indra's PearlsIndra's Pearls (book)Indra's Pearls: The Vision of Felix Klein is a geometry book written by David Mumford, Caroline Series and David Wright, and published by Cambridge University Press in 2002....
, David MumfordDavid MumfordDavid Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
and others investigated various properties of Möbius transformation and Schottky groupSchottky groupIn mathematics, a Schottky group is a special sort of Kleinian group, first studied by .-Definition:Fix some point p on the Riemann sphere...
using computer generated images of the groups which: furnished convincing evidence for many conjectures and lures to further exploration.
- In Indra's Pearls
Open problems
Some relations have been shown to hold to very high precision, but no formal proof has yet been found; one example is:
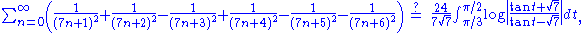
which has been verified to 20,000 digits.
Plausible but false examples
Some plausible relations hold to a high degree of accuracy, but are still not true. One example is:
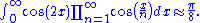
The two sides of this expression only differ after the 42nd decimal place.
Another example is that the maximum heightHeight of a polynomialIn mathematics, the height and length of a polynomial P with complex coefficients are measures of its "size".For a polynomial P given byP = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n ,...
(maximum absolute value of coefficients) of all the factors of xn − 1 appears to be the same as height of nth cyclotomic polynomialCyclotomic polynomialIn algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
. This was shown by computer to be true for n < 10000 and was expected to be true for all n. However, a larger computer search showed that this equality fails to hold for n = 14235, when the height of the nth cyclotomic polynomial is 2, but maximum height of the factors is 3.
Practitioners
The following mathematicianMathematicianA mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s and computer scientistComputer scientistA computer scientist is a scientist who has acquired knowledge of computer science, the study of the theoretical foundations of information and computation and their application in computer systems....
s have made significant contributions to the field of experimental mathematics:
See also
- Computer-aided proof
- Proofs and RefutationsProofs and RefutationsProofs and Refutations is a book by the philosopher Imre Lakatos expounding his view ofthe progress of mathematics. The book is written as a series of Socratic dialogues involving a group of students who debate the proof of the Euler characteristic defined for the polyhedron...
- Experimental Mathematics (journal)Experimental Mathematics (journal)Experimental Mathematics is a quarterly scientific journal of mathematics published by A K Peters, Ltd. until 2004, now by Taylor & Francis. The journal publishes papers in experimental mathematics, broadly construed...
- Institute for Experimental MathematicsInstitute for Experimental MathematicsThe Institute for Experimental Mathematics was founded, with the support of the VolkswagenFoundation, as a central scientific facility of the former University of Essen, now University of Duisburg-Essen in 1989. With the addition of the Alfried Krupp von Bohlen und Halbach Foundation Chair on 1...
External links
- Experimental Mathematics (Journal)
- Centre for Experimental and Constructive Mathematics (CECM) at Simon Fraser UniversitySimon Fraser UniversitySimon Fraser University is a Canadian public research university in British Columbia with its main campus on Burnaby Mountain in Burnaby, and satellite campuses in Vancouver and Surrey. The main campus in Burnaby, located from downtown Vancouver, was established in 1965 and has more than 34,000...
- Collaborative Group for Research in Mathematics Education at University of SouthamptonUniversity of SouthamptonThe University of Southampton is a British public university located in the city of Southampton, England, a member of the Russell Group. The origins of the university can be dated back to the founding of the Hartley Institution in 1862 by Henry Robertson Hartley. In 1902, the Institution developed...
- Recognizing Numerical Constants by David H. BaileyDavid H. BaileyDavid Harold Bailey is a mathematician and computer scientist. He received his B.S. in mathematics from Brigham Young University in 1972 and his Ph.D. in mathematics from Stanford University in 1976...
and Simon PlouffeSimon PlouffeSimon Plouffe is a Quebec mathematician born on June 11, 1956 in Saint-Jovite, Quebec. He discovered the formula for the BBP algorithm which permits the computation of the nth binary digit of π, in 1995... - Psychology of Experimental Mathematics
- Experimental Mathematics Website (Links and resources)
- An Algorithm for the Ages: PSLQ, A Better Way to Find Integer Relations
- Experimental Algorithmic Information Theory
- Sample Problems of Experimental Mathematics by David H. BaileyDavid H. BaileyDavid Harold Bailey is a mathematician and computer scientist. He received his B.S. in mathematics from Brigham Young University in 1972 and his Ph.D. in mathematics from Stanford University in 1976...
and Jonathan M. BorweinJonathan BorweinJonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H... - Ten Problems in Experimental Mathematics by David H. BaileyDavid H. BaileyDavid Harold Bailey is a mathematician and computer scientist. He received his B.S. in mathematics from Brigham Young University in 1972 and his Ph.D. in mathematics from Stanford University in 1976...
, Jonathan M. BorweinJonathan BorweinJonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...
, Vishaal Kapoor, and Eric W. WeissteinEric W. WeissteinEric W. Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science . He currently works for Wolfram Research, Inc.-Education:... - Institute for Experimental Mathematics at University of Duisburg-EssenUniversity of Duisburg-EssenThe University Duisburg-Essen is a public university in Duisburg and Essen, North Rhine-Westphalia, Germany and a member of the new founded University Alliance Metropolis Ruhr....
- Visual investigations

