
Mathematical descriptions of physical laws
Encyclopedia
Physical laws are often summarized by a single equation, or at least a small set of equations. This article tabulates many of the important bands of physics where such laws occur.
can be written as a conservation law
(also as continuity equation
). The formalism of how conservation laws can be used is given below. See also Noether's theorem
.
Then we have the following equations.
In the table below, the fluxes, flows and continuity equations have been collected for comparison. Also alternative forms using currents have been included; often these forms are used in introductory transport mechanics since they are simply statements which relate current and flux, simply by conservation of the quantity as it flows. The nomenclature is very similar throughout the equations, to make clear the nature of transport much of the nomenclature been re-stated.
Unprimed quantities refer to position, velocity and acceleration in one frame F; primed quantities refer to position, velocity and acceleration in another frame F' moving at translational velocity V or angular velocity Ω relative to F. Conversely F moves at velocity (—V or —Ω) relative to F'. The situation is similar for relative accelerations.
 = Internal energy
= Internal energy
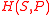 = Enthalpy
= Enthalpy
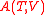 = Helmholtz free energy
= Helmholtz free energy
 = Gibbs free energy
= Gibbs free energy
Main article: Einstein field equations
(ETF), Gravitomagnetism
(GEM)
In a relatively flat spacetime due to weak gravitational fields (by General Relativity), the following gravitational analogues of Maxwell's equations can be found, to describe an analogous Gravitomagnetic Field. They are well established by the theory, but have yet to be verified by experiment.
), are true for any central forces.
For Kepler's 1st law, the equation is nothing physically fundamental; simply the polar equation
of an ellipse
where the pole (origin of polar coordinate system) is positioned at a focus of the ellipse, centred on the central star.
e = (elliptic) eccentricity
a = elliptic semi-major axes = planet aphelion
b = elliptic semi-minor axes = planet perihelion
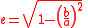
{2m} \,\!
|-
|Kepler's 3rd Law
|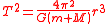
|-
|}
Monopoles Inclusion
To introduce monopoles mathematically, magnetic pole strength
qm (AKA magnetic charge or monopole charge, all synonymous) is defined, treating magnetic poles analogously to electric charges - see section below. Pole srength can be quantified into volume densities, currents and current densities just like electric charge.
The mathematical convention is: north charge N; qm > 0, south charge S; qm < 0, neutral charge; qm = 0 (equivalent to no net magnetic charge, or none at all).
From the SI system two units are possible, Wb (Weber
) and A m (Ampere
-metre
). Dimensional analysis
leads to the conversion:
Maxwell's Equations would become one of the columns in the table below, at least theoretically. Subscripts e are electric charge quantities; subscripts m are magnetic charge quantities. They are consistent if no magnetic monopoles exist, since the monopole quantities are then zero and the equations reduce to the original form of Maxwell's equations.
Let:
α = Mass, electric charge or magnetic monopole strength,
Λ = Gravitational, electric field or magnetic field,
F = Force,
Π = Mass moment, electric dipole due to charges, magnetic moment due to current or monopoles,
d = Pole separation for electric/magnetic dipoles,
r = Position vector,
X = Proportionality constants related to other physical constants,
Y = Physical constant, gravitational constant
G, vacuum permittivity ε0, vacuum permeability
μ0,
ФΛ = Field flux,
n, m = any from +1, 0, −1
and using the same notation as before in the General principles section above, we have the following.
= \frac{\mathbf{r}_{\rm i} - \mathbf{r}_{\rm j}}{\left | \mathbf{r}_{\rm i} - \mathbf{r}_{\rm j} \right |} \,\!
|-
|Mass moments or electric/magnetic dipole moments
|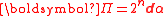
|-
|Mass moment density, electric or magnetic dipole moment densities (polarization/ magnetization)
|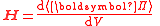
The average moment is simply:

|-
|Field flux
|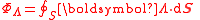
|-
|"Gaussian law"
|Equivalent forms (by the divergence theorem) are:
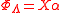
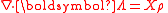
|-
|}
\left [ \cos \alpha_0 - \cos \alpha \right ] \mathrm{d}S \,\!
where
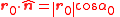


|-
| r0 = position from source to aperture, incident on it
r = position from aperture diffracted from it to a point
α0 = incident angle with respect to the normal, from source to aperture
α = diffracted angle, from aperture to a point
S = imaginary surface bounded by aperture
 = unit normal vector to the aperture
= unit normal vector to the aperture
|-
| Kirchhoff's diffraction formula
|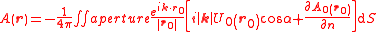
|-
|}
These ratios are sometimes also used, following simply from other definitions of refractive index, wave phase velocity, and the luminal speed equation;

where:
ε = permittivity
of medium,
μ = permeability
of medium,
λ = wavelength
of light in medium,
v = speed of light
in media.
Commonly used corollaries of Schrödinger's equation are obtained in this way:
- A free particle corresponds to zero potential energy.
A boost B(v) in any arbitrary direction at velocity v = (vx, vy, vz), or equivalently β = (βx, βy, βz), without rotation, is given by:

where


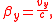

 , and
, and 
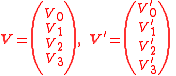
Conservation and continuity
All conserved quantitiesConserved quantity
In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...
can be written as a conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
(also as continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
). The formalism of how conservation laws can be used is given below. See also Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
.
| Let | so that |
| S = Closed surface of region to calculate flux, arbitrary but fixed for calculation, R = Region of space bounded by S containing total amount of quantity Q, which occupies the closed system, A = surface or cross-sectional area through which flows pass through, 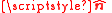 = unit normal to A, = unit normal to A,A = vector area, V = Volume of closed system, r = position vector, t = time, q = any conserved quantity as a function of space and time within the closed system (since it may flow throughout, but the total amount in the system is still constant and independent of space and time), Q = total amount of q for system (constant), I = current of q, J = current density of q,  = unit vector in direction of J, = unit vector in direction of J,ρ = volume density of q T = time taken for all of z to pass a boundary (including a point), Σ = Total generation (positive) or removal (negative) of q per unit time by the sources and sinks in the volume V, σ = Total generation (positive) or removal (negative) of q per unit volume per unit time by the sources and sinks in the volume V N = number of discrete constituents of the system, e.g. particles possessing momenta |
  , , 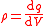 , , , ,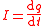 As a scalar  or vector or vector 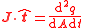 (θ = angle between J and normal to A) |
Then we have the following equations.
Summary of conservative formalisms
The following appear trivial and self-evident, but often calculations for conservative situations are applied in one of these forms.| Equation type | Discrete equation | Continuum equation |
|---|---|---|
| Constancy equation | All changes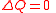 |
Differential changes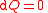 |
| System equation/s |  |
 |
| Time derivatives, Current |
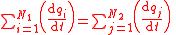  |
 |
| Time–area derivatives, Current density, flux |
 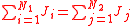  |
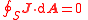 by the divergence theorem Divergence theorem In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem... ;  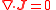 |
Summary of classical continuity equations
The general continuity equation can be written in differential or integral form:  |
In the table below, the fluxes, flows and continuity equations have been collected for comparison. Also alternative forms using currents have been included; often these forms are used in introductory transport mechanics since they are simply statements which relate current and flux, simply by conservation of the quantity as it flows. The nomenclature is very similar throughout the equations, to make clear the nature of transport much of the nomenclature been re-stated.
| Phyics, conserved quantity | Conserved quantity q | Volume density ρ (of q) | Flux J (of q) | Vector DE | Conservative equation |
|---|---|---|---|---|---|
| Hydrodynamics, fluid |
m = mass (kg) | ρ = volume mass density (kg m-3) | ρ u, where u = velocity field of fluid (m s-1) |
 |
 jm = mass current at the cross-section (kg s-1) |
| Electromagnetism, electric charge | q = electric charge (C) | ρ = volume electric charge density (C m-3) | J = electric current density (A m-2) | 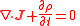 |
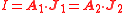 I = electric current at the cross-section (A) |
| Thermodynamics, energy | E = energy (J) | u = volume energy density (J m-3) | q = heat flux (W m-2) | 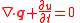 |
 P = thermal current Power (physics) In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit... at the cross-section (W) |
| Quantum mechanics, probability | p = Pr(x,t) = probability distribution Probability distribution In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values.... |
P = P(x,t) = probability density function (m-3) | j = probability current/flux |  |
|
Principle of least action
A system always minimizes the action associated with all parts of the system. Various minimized action formulations are given, all of course equivalent.| Formulation | Nomenclature | Equations |
|---|---|---|
| Statement |  = action = action |
 |
| Maupertuis'-Euler | t = time Time Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects.... , t1, t2 = initial and final times, T = Kinetic energy Kinetic energy The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes... |
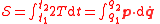 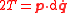 |
| Jacobi's | s = arc length Arc length Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves... , C = curve, T = Kinetic energy V = Potential energy Potential energy In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule... E = Total mechanical energy |
  |
| Lagrange | L = Lagrangian Lagrangian The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as... |
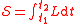 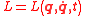 |
Galilean frame transforms
For classical (Galileo-Newtonian) mechanics, the transformation law from one inertial or accelerating (including rotation) frame (reference frame travelling at constant velocity - including zero) to another is the Galilean transform.Unprimed quantities refer to position, velocity and acceleration in one frame F; primed quantities refer to position, velocity and acceleration in another frame F' moving at translational velocity V or angular velocity Ω relative to F. Conversely F moves at velocity (—V or —Ω) relative to F'. The situation is similar for relative accelerations.
| Motion of entities | Inertial frames | Accelerating frames | |
|---|---|---|---|
| Translation V = Constant relative velocity between two inertial frames F and F'. A = (Variable) relative acceleration between two accelerating frames F and F'. |
Relative position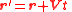 Relative velocity  Equivalent accelerations  |
Relative accelerations Apparent/ficticous forces 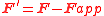 |
|
| As measured in frame F: r = position v = velocity a = acceleration F = force |
As measured in frame F': r' = position v' = velocity a' = acceleration F' = force Fapp = apparent forces |
||
| Rotation Ω = Constant relative angular velocity between two frames F and F'. Λ = (Variable) relative angular acceleration between two accelerating frames F and F'. |
Relative angular position Relative velocity 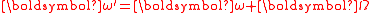 Equivalent accelerations  |
Relative accelerations Apparent/ficticous torques  |
|
As measured in frame F: θ = angular position, angle ω = angular velocity α = angular acceleration τ = torque |
As measured in frame F': r' = angular position ω' = angular velocity α' = angular acceleration τ' = torque τapp = apparent torque |
||
Laws of classical mechanics
The following general approaches to classical mechanics are summarized below in the order of establishment. They are equivalent formulations, Newton's is very commonly used due to simplicity, but Hamilton's and Lagrange's equations are more general, and their range can extend into other branches of physics with suitable modifications.| Laws | Equation |
|---|---|
| Newton's laws | The laws can be summarized by two equations: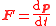  For a dynamical system the two equations (effectively) combine into one:  |
| p = momentum of body, Fij = force ON body i BY body j, Fij = force ON body j BY body i, FE = resultant external force (due to any agent not part of system). Body i does not exert a force on itself. |
|
| Euler-Lagrange equations | Euler-Lagrange equation system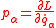 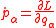 Euler-Lagrange equation  |
| qi = generalized coordinates, pi = generalized momenta |
|
| Hamilton's equation system |  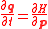 The Hamiltonian as a function of generalized coordinates and momenta has the general form: 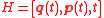 |
| Appell's equation | 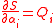 where:  |
| Qi = generalized force αi = generalized acceleration ai = acceleration of particle |
|
Main laws
| Property/effect | Equation |
|---|---|
| Zeroth law of thermodynamics Zeroth law of thermodynamics The zeroth law of thermodynamics is a generalization principle of thermal equilibrium among bodies, or thermodynamic systems, in contact.The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.Systems are said to... (systems in thermal equilibrium) |
 |
| First law of thermodynamics First law of thermodynamics The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed... |
 Internal energy increase 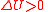 , decrease , decrease 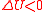 Heat energy transferred to system  , from system , from system  Work done transferred to system 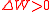 by system by system 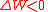 |
| Second Law of Thermodynamics Second law of thermodynamics The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and... |
 |
| Third Law of Thermodynamics Third law of thermodynamics The third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:... |
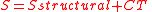 |
Extensions of the laws
| Property or effect | Equation |
|---|---|
| Fundamental thermodynamic relation (systems in thermal equilibrium) |  |
| Onsager reciprocal relations Onsager reciprocal relations In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.... |
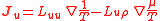 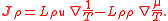 |
| u = Energy Density (J m−3) J = Energy Flux Density (W m−2) L = Reciprocity Coefficients (K kg m−3) |
|
Maxwell's relations
The potentials as functions of their natural variables are: = Internal energy
= Internal energyInternal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
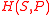 = Enthalpy
= EnthalpyEnthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
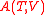 = Helmholtz free energy
= Helmholtz free energyHelmholtz free energy
In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
 = Gibbs free energy
= Gibbs free energyGibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
 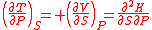 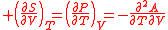 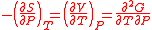 |
Modern laws
ETF and GEM EquationsMain article: Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
(ETF), Gravitomagnetism
Gravitomagnetism
Gravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
(GEM)
In a relatively flat spacetime due to weak gravitational fields (by General Relativity), the following gravitational analogues of Maxwell's equations can be found, to describe an analogous Gravitomagnetic Field. They are well established by the theory, but have yet to be verified by experiment.
| Laws | Nomenclature | Equations |
|---|---|---|
| Einstein Tensor Field (ETF) Equations | Λ = Cosmological Constant Rμν = Ricci Curvature Tensor Tμν = Stress-Energy Tensor gμν = The Metric Tensor Gμν = Einstein Tensor |
 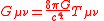 |
| GEM Equations | g = Gravitational Field ξ = Gravitomagnetic Field |
   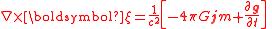 |
| Gravitomagnetic Lorentz Force | Ω = Gravitational Torsion Field | 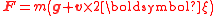  |
Classical laws
It can be found that Kepler's Laws, though originally discovered from planetary observations (also due to Tycho BraheTycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
), are true for any central forces.
For Kepler's 1st law, the equation is nothing physically fundamental; simply the polar equation
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
of an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
where the pole (origin of polar coordinate system) is positioned at a focus of the ellipse, centred on the central star.
e = (elliptic) eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
a = elliptic semi-major axes = planet aphelion
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
b = elliptic semi-minor axes = planet perihelion
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
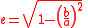
| Property or effect | Equation |
|---|---|
| Newton's law of universal gravitation Newton's law of universal gravitation Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them... |
 For a non uniform mass distribution this becomes: 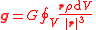 |
| ρ = Local mass density of body V = Volume of body |
|
| Gauss' law for gravity Gauss' law for gravity In physics, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics which is essentially equivalent to Newton's law of universal gravitation... |
 |
| Kepler's 1st Law Planets move in an ellipse, with the star at a focus |
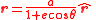 |
| Kepler's 2nd Law |
|-
|Kepler's 3rd Law
|
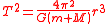
|-
|}
Maxwell's equations
No Magnetic Monopoles| Name | Differential form |
|---|---|
| Gauss's law for electrostatics | 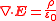 |
| Gauss's law for magnetostatics |  |
| Maxwell–Faraday law (Faraday's law of induction) |
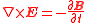 |
| Maxwell-Ampère circuital law (Ampere's Law with Maxwell's correction) |
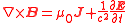 |
| Lorentz force law |  |
Monopoles Inclusion
To introduce monopoles mathematically, magnetic pole strength
Magnetic pole strength
Magnetic pole strength is a physical quantity used to measure the strength of the pole of a bar magnet...
qm (AKA magnetic charge or monopole charge, all synonymous) is defined, treating magnetic poles analogously to electric charges - see section below. Pole srength can be quantified into volume densities, currents and current densities just like electric charge.
The mathematical convention is: north charge N; qm > 0, south charge S; qm < 0, neutral charge; qm = 0 (equivalent to no net magnetic charge, or none at all).
From the SI system two units are possible, Wb (Weber
Weber (unit)
In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :...
) and A m (Ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
-metre
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
). Dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
leads to the conversion:
 |
Maxwell's Equations would become one of the columns in the table below, at least theoretically. Subscripts e are electric charge quantities; subscripts m are magnetic charge quantities. They are consistent if no magnetic monopoles exist, since the monopole quantities are then zero and the equations reduce to the original form of Maxwell's equations.
| Name | Weber (Wb) | Ampere meter (A m) convention |
|---|---|---|
| Gauss's law for electrostatics | 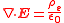 |
 |
| Gauss's law for magnetostatics |  |
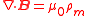 |
| Faraday's law of induction | 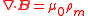 |
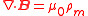 |
| Ampère's law |  |
 |
| Lorentz force equation | 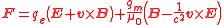 |
 |
Pre-Maxwell laws
These laws are not fundamental, since they can be derived from Maxwell's Equations. Coulomb's Law can be found from Gauss' Law (electrostatic form) and the Biot-Savart Law can be deduced from Ampere's Law (magnetostatic form). Lenz' Law and Faraday's Law can be incorporated into the Maxwell-Faraday equation. Nonetheless they are still very effective for simple calculations.| Name | Equation |
|---|---|
| Coulomb's Law Coulomb's law Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism... |
|
| Biot-Savart law Biot-Savart law The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant... |
|
| Lenz's law Lenz's law Lenz's law is a common way of understanding how electromagnetic circuits must always obey Newton's third law and The Law of Conservation of Energy... |
The magnetic flux set up by the current in a conductor tends to oppose that current. |
| Kirchoff's Laws | emf loop rule around any closed circuit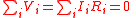 Current law at junctions  |
Parallels between classical gravitation and electromagnetism
Below the mathematics can only be incorporated into magnetism if magnetic monopoles exist. If they do not, then as stated in the above Laws of electromagnetism section the pole strength is zero and monopole quantities disappear.Let:
α = Mass, electric charge or magnetic monopole strength,
Λ = Gravitational, electric field or magnetic field,
F = Force,
Π = Mass moment, electric dipole due to charges, magnetic moment due to current or monopoles,
d = Pole separation for electric/magnetic dipoles,
r = Position vector,
X = Proportionality constants related to other physical constants,
Y = Physical constant, gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G, vacuum permittivity ε0, vacuum permeability
Vacuum permeability
The physical constant μ0, commonly called the vacuum permeability, permeability of free space, or magnetic constant is an ideal, physical constant, which is the value of magnetic permeability in a classical vacuum...
μ0,
ФΛ = Field flux,
n, m = any from +1, 0, −1
and using the same notation as before in the General principles section above, we have the following.
| Property or effect | Equation |
|---|---|
| Constants |  |
| Quantification: volume densities, currents, current densities | 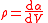 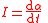 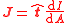 |
| Force due to field |
|-
|Mass moments or electric/magnetic dipole moments
|
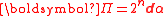
|-
|Mass moment density, electric or magnetic dipole moment densities (polarization/ magnetization)
|
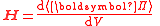
The average moment is simply:

|-
|Field flux
|
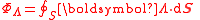
|-
|"Gaussian law"
|Equivalent forms (by the divergence theorem) are:
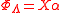
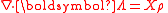
|-
|}
Photonics
Subscripts 1 and 2 refer to initial and final optical media respectivley.| Name | Equations |
|---|---|
| Law of reflection |  |
| θ = angle of refraction relative to the interface normal | |
| Law of refraction, Snell's law Snell's law In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass... |
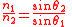 |
| n = refractive index Refractive index In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium.... of medium |
|
| Angle of total polarisation | 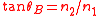 |
| θB = Reflective polarization angle, Brewster's angle Brewster's angle Brewster's angle is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly... |
|
| intensity Intensity (physics) In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech... from polarized light, Malus' law |
 |
| I0 = Initial intensity, I = Transmitted intensity, θ = Polarization angle between polarizer Polarizer A polarizer is an optical filter that passes light of a specific polarization and blocks waves of other polarizations. It can convert a beam of light of undefined or mixed polarization into a beam with well-defined polarization. The common types of polarizers are linear polarizers and circular... transmission axes and electric field vector |
|
| Bragg's law Bragg's law In physics, Bragg's law gives the angles for coherent and incoherent scattering from a crystal lattice. When X-rays are incident on an atom, they make the electronic cloud move as does any electromagnetic wave... (solid state diffraction) |
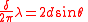 For constructive interference: 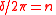 For destructive interference:  where  |
| d = lattice spacing δ = phase differance between two waves |
|
| Huygen-Fresnel-Kirchhoff principle |
where
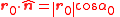


|-
| r0 = position from source to aperture, incident on it
r = position from aperture diffracted from it to a point
α0 = incident angle with respect to the normal, from source to aperture
α = diffracted angle, from aperture to a point
S = imaginary surface bounded by aperture
 = unit normal vector to the aperture
= unit normal vector to the aperture|-
| Kirchhoff's diffraction formula
Kirchhoff's diffraction formula
Kirchhoff's diffraction formula can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen...
|
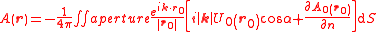
|-
|}
These ratios are sometimes also used, following simply from other definitions of refractive index, wave phase velocity, and the luminal speed equation;

where:
ε = permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of medium,
μ = permeability
Permeability
Permeability, permeable and semipermeable may refer to:*Permeability , the degree of magnetization of a material in response to a magnetic field...
of medium,
λ = wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of light in medium,
v = speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in media.
Radiation
| Name | Equations |
|---|---|
| Radioactive decay Radioactive decay Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom... |
Statistical decay of a radionuclide:  |
| N = N(t) = Number of atoms at time t t = Time (s) λ = Decay constant (s-1) |
|
| Stefan–Boltzmann law | 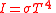 |
| I = Intensity (W m-2) | |
| Wien's displacement law Wien's displacement law Wien's displacement law states that the wavelength distribution of thermal radiation from a black body at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength is displaced on the graph... |
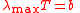 |
| b = Wein constant (m K) | |
| Planck's law |    |
| I = Specific radiative intensity Specific radiative intensity Specific intensity is a fundamental quantity used in theoretical physics that fully describes the field of classical electromagnetic radiation of any kind, including thermal radiation and light. It is a description based on radiometry rather than Maxwellian electromagnetic fields or photon... (W m–2 Hz–1 sr–1) |
|
Wavefunction equations
| Name | Equation |
|---|---|
| Schrödinger equation Schrödinger equation The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time.... |
General classical form for all wavefunctions ψ = ψ(r, t): |
| Dirac equation Dirac equation The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and... |
For elementary spin-1/2 particles Spin-½ In quantum mechanics, spin is an intrinsic property of all elementary particles. Fermions, the particles that constitute ordinary matter, have half-integer spin. Spin-½ particles constitute an important subset of such fermions. All known elementary fermions have a spin of ½.- Overview :Particles... : 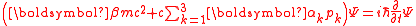 Dirac matrices:   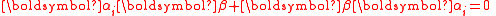 |
| Klein–Gordon equation | General form for all relativistic wavefunctions ψ = ψ(r, t):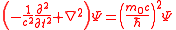 Can be obtained by inserting the quantum operators Operator (physics) In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information.... into the momentum-energy invariant of relativistic mechanics: 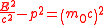 |
Commonly used corollaries of Schrödinger's equation are obtained in this way:
- A free particle corresponds to zero potential energy.
Wave–particle duality
| Property/effect | Equation |
|---|---|
| Planck–Einstein equation |   |
| de Broglie wavelength |   |
| Heisenberg's uncertainty principle |   |
Special relativity
Fundamental invariance and unification of space-time and energy-mass-momentum are given below. Both 4-vectors are very analogous, leading to analogous expressions using only the 4-vector dot product. The relativistic analogue to the classical Galilean transformation is the Lorentz transformation.Lorentz frame tranforms
Let V = any 4-vector.A boost B(v) in any arbitrary direction at velocity v = (vx, vy, vz), or equivalently β = (βx, βy, βz), without rotation, is given by:

where


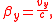

 , and
, and 
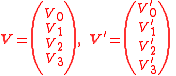
4-vectors and frame-invariant results
| Property/effect | 3-vectors | 4-vectors | Invariant result |
|---|---|---|---|
| Time and proper time | 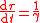 |
||
| Space-time | 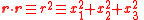 |
  |
|
| τ = Proper time χ = Proper length 3-Position: r = (x1, x2, x3) 4-Position: R = (ct, x1, x2, x3) |
|||
| Velocity transform | 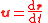 |
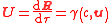 |
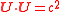 |
| 3-Velocity: u = (u1, u2, u3) 4-Velocity: U = (u0, u1, u2, u3) |
|||
| Momentum-energy invariance |   |
 |
 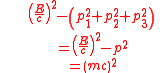 which leads to: 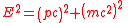 |
| E = total energy m = invariant mass 3-Momentum: p = (p1, p2, p3) 4-Position: P = (E/c, p1, p2, p3) |
|||
| Acceleration transform | 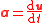 |
 |
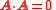 |
| 3-Acceleration: a = (a1, a2, a3) 4-Acceleration: A = (a0, a1, a2, a3) |
|||
| Force transform |  |
 |
 |
| 3-Acceleration: f = (f1, f2, f3) 4-Acceleration: F = (f0, f1, f2, f3) |
|||
Particle Physics
| Name | Equations |
|---|---|
| Strong force | 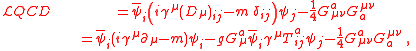 |
| Electroweak interaction Electroweak interaction In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different... |
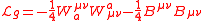 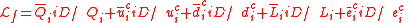   |
| Quantum electrodynamics Quantum electrodynamics Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved... |
 |

