
Zeroth law of thermodynamics
Encyclopedia
The zeroth law of thermodynamics
is a generalization principle of thermal equilibrium
among bodies, or thermodynamic system
s, in contact.
The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.
Systems are said to be in thermal equilibrium if they do not actually exchange heat
, and, if they are not already connected by a conductor of heat or pathway for exchange of thermal radiation, would not do so if they were so connected. The law implies that thermal equilibrium between systems is a transitive relation
, which affords the definition of an empirical physical parameter, called temperature
. The temperatures are equal for all systems in thermal equilibrium. The law permits the construction of a thermometer
to measure this property.
when it experiences no net change in thermal energy. If A, B, and C are distinct thermodynamic system
s, the zeroth
law of thermodynamics
can be expressed as:
This statement asserts that thermal equilibrium is a Euclidean relation
between thermodynamic systems. If we also grant that all thermodynamic systems are in thermal equilibrium with themselves, then thermal equilibrium is also a reflexive relation
. Relations
that are both reflexive and Euclidean are equivalence relation
s. One consequence of this reasoning is that thermal equilibrium is a transitive relation
ship: If A is in thermal equilibrium with B and B is in thermal equilibrium with C, then A is in thermal equilibrium with C. Another consequence is that the equilibrium relationship is symmetric: If A is in thermal equilibrium with B, then B is in thermal equilibrium with A. Thus we may say that two systems are in thermal equilibrium with each other, or that they are in mutual equilibrium. Implicitly assuming both reflexivity and symmetry, the zeroth law is therefore often expressed as:
Again, implicitly assuming both reflexivity and symmetry, the zeroth law is occasionally expressed as the transitive relationship
or photon emissions, for example) between them do not lead to a net change in the total energy summed over all systems. A simple example illustrates why the zeroth law is necessary to complete the equilibrium description.
Consider N systems in adiabatic
isolation from the rest of the universe, i.e. no heat exchange is possible outside of these N systems, all of which have a constant volume
and composition, and which can only exchange heat
with one another.
The combined First and Second Laws relate the fluctuations in total energy, , to the temperature of the ith system,
, to the temperature of the ith system, 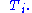 and the entropy
and the entropy
fluctuation in the ith system,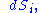 as follows:
as follows: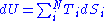 .
.
The adiabatic
isolation of the system from the remaining universe requires that the total sum of the entropy fluctuations vanishes, or: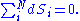
That is, entropy can only be exchanged between the N systems. This constraint can be used to rearrange the expression for the total energy fluctuation and obtain: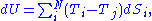
where is the temperature of any system j we may choose to single out among the N systems. Finally, equilibrium requires the total fluctuation in energy to vanish, in which case:
is the temperature of any system j we may choose to single out among the N systems. Finally, equilibrium requires the total fluctuation in energy to vanish, in which case: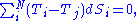
which can be thought of as the vanishing of the product of an antisymmetric matrix and a vector of entropy fluctuations
and a vector of entropy fluctuations 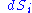 . In order for a non-trivial solution to exist,
. In order for a non-trivial solution to exist,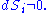
That is, the determinant
of the matrix formed by must vanish for all choices of N. However, according to Jacobi's theorem, the determinant of a NxN antisymmetric matrix is always zero if N is odd, although for N even we find that all of the entries must vanish,
must vanish for all choices of N. However, according to Jacobi's theorem, the determinant of a NxN antisymmetric matrix is always zero if N is odd, although for N even we find that all of the entries must vanish,  , in order to obtain a vanishing determinant. Hence
, in order to obtain a vanishing determinant. Hence 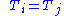 at equilibrium. This non-intuitive result means that an odd number of systems are always in equilibrium regardless of their temperatures and entropy fluctuations, while equality of temperatures is only required between an even number of systems to achieve equilibrium in the presence of entropy fluctuations.
at equilibrium. This non-intuitive result means that an odd number of systems are always in equilibrium regardless of their temperatures and entropy fluctuations, while equality of temperatures is only required between an even number of systems to achieve equilibrium in the presence of entropy fluctuations.
The zeroth law solves this odd vs. even paradox, because it can readily be used to reduce an odd-numbered system to an even number by considering any three of the N systems and eliminating one by application of its principle, and hence reduce the problem to even N which subsequently leads to the same equilibrium condition that we expect in every case, i.e.,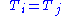 . The same result applies to fluctuations in any extensive quantity, such as volume (yielding the equal pressure condition), or fluctuations in mass (leading to equality of chemical potentials). Hence the zeroth law has implications for a great deal more than temperature alone. In general, we see that the zeroth law breaks a certain kind of asymmetry present in the First and Second Laws.
. The same result applies to fluctuations in any extensive quantity, such as volume (yielding the equal pressure condition), or fluctuations in mass (leading to equality of chemical potentials). Hence the zeroth law has implications for a great deal more than temperature alone. In general, we see that the zeroth law breaks a certain kind of asymmetry present in the First and Second Laws.
s to provide such a labeling, which yield any number of possible empirical temperature scales, and justifies the use of the second law of thermodynamics
to provide an absolute, or thermodynamic temperature
scale. Such temperature scales bring additional continuity and ordering (i.e., "hot" and "cold") properties to the concept of temperature.
In the space of thermodynamic parameters, zones of constant temperature form a surface, that provides a natural order of nearby surfaces. One may therefore construct a global temperature function that provides a continuous ordering of states. The dimensionality of a surface of constant temperature is one less than the number of thermodynamic parameters, thus, for an ideal gas described with three thermodynamic parameters P, V and n, it is a two-dimension
al surface.
For example, if two systems of ideal gases are in equilibrium, then P1V1/N1 = P2V2/N2 where Pi is the pressure in the ith system, Vi is the volume, and Ni is the amount (in mole
s, or simply the number of atoms) of gas.
The surface PV/N = const defines surfaces of equal thermodynamic temperature, and one may label defining T so that PV/N = RT, where R is some constant. These systems can now be used as a thermometer to calibrate other systems. Such systems are known as "ideal gas thermometers".
and to Newton. Carnot
took it as a presupposition for his work. Thermometers may be described as empirical or absolute. Absolute thermometers are calibrated numerically by the thermodynamic absolute temperature scale
. It was not until the middle of the nineteenth century that absolute thermodynamic temperature was recognized, long after the recognition of empirical thermometry.
Empirical thermometry recognizes hotness as a fundamental character of temperature and thermometers. Empirical thermometers are not in general necessarily in exact agreement with each other or with absolute thermometers as to their numerical scale readings, but to qualify as thermometers at all they must agree with absolute thermometers and with each other in the following way: given any two bodies isolated in their separate respective thermodynamic equilibrium states, all thermometers agree as to which of the two has the higher temperature, or that the two have equal temperatures. For any two empirical thermometers, this does not require that the relation between their numerical scale readings be linear, but it does require that relation to be strictly monotonic.
Truesdell
reports that Rankine
wrote in 1853:
Discussing the concept of temperature, James Clerk Maxwell
in 1872 wrote: "If when two bodies are placed in thermal communication, one of the two bodies loses heat, and the other gains heat, that body which gives out heat is said to have a higher temperature than that which receives heat from it." He drew the corollary "If when two bodies are placed in thermal communication neither of them loses or gains heat, the two bodies are said to have equal temperatures or the same temperature. The two bodies are then said to be in thermal equilibrium."
Further, Maxwell stated, as the "Law of equal temperatures" the following triviality: "Bodies whose temperatures are equal to that of the same body have themselves equal temperatures". Maxwell then offered an argument that this statement was "not a truism". Later in the same text, Maxwell wrote: "Hence the result of the conduction and radiation of heat from one part of a system to another is to diminish the entropy of the system, or the energy, available as work, which can be obtained from the system." This statement was surrounded in Maxwell's text by several others like it that show that it was no slip of the pen. In the same textbook, Maxwell wrote that he was following Tait in re-defining the word entropy that had been introduced by Clausius. In contrast with what Maxwell wrote then, Tait had changed his mind by 1884 when in his text he accepted Clausius's original definition of entropy.
Subsequent writers made statements like Maxwell's. Tait in 1884 wrote "if A is at the same temperature as B and also at the same temperature as C — no transfer of heat takes place between B and C, whatever be these bodies." A similar statement was made by Max Planck
in 1897, not labeled as a law but as an important proposition: "If a body, A, be in thermal equilibrium with two other bodies, B and C, then B and C are in thermal equilibrium with one another." Planck repeated this important proposition in the seventh edition of his treatise in 1922.
The title "zeroth law of thermodynamics" began to appear in textbooks to refer to statements of this kind, though now stripped of their explicit reference to heat; their implicit dependence on the notion of heat could not be removed because they rely on the concept of thermal equilibrium which in turn relies on the concept of transfer of heat by conduction or radiation, the presence or absence of which must be empirically recognizable in order to make the concept of thermal equilibrium empirically recognizable. An early example is in the textbook of statistical thermodynamics of Fowler and Guggenheim (1939/1965). Their focus of interest in that book was homogeneous systems (page 1), which they termed 'assemblies'. They dealt with assemblies that were either completely homogeneous or that could be divided into homogeneous parts, called phases (page 58). For their macroscopic thermodynamic account of phenomena, they started by accepting, on empirical physical grounds, the presupposed notions of thermal insulation, thermal contact, and thermal equilibrium (page 56). They emphasized that these notions "can be defined without any reference to temperature" (page 56). Moreover, they gave at this stage of their development of their theory no hint of the notion of heat transfer. On page 56, they wrote:
They then proposed that "it may be shown to follow that the condition for thermal equilibrium between several assemblies is the equality of a certain single-valued function of the thermodynamics states of the assemblies, which may be called the temperature t, any one of the assemblies being used as a "thermometer" reading the temperature t on a suitable scale. This postulate of the "Existence of temperature" could with advantage be known as the zeroth law of thermodynamics" (page 56). They did not there state any reason why such a function should have values in a scale consisting of a continuous succession of numbers or that it should have anything to do with heat. Their thinking was apparently conditioned by their asserted belief that "The most logically satisfactory formulation [of homogeneous system macroscopic thermodynamics] is undoubtedly that of Carathéodory" (page 56). Though they thus apparently professed concern for logicality, they had no apparent compunction about immediately assuming, without apparent justification, that their postulated "temperatures" should exist on a numerical scale, provided for example by "the measured volume of a constant quantity of any chosen substance at constant pressure" (page 56). No worries about pesky but relevant physical realities such as the anomalous behaviour of water that concerned the nineteenth century thermodynamicists, because around 4 C it does not provide a valid empirical temperature. No mention that it would therefore be safer to refer to a permanent gas as a thermometric material. The approach of Fowler and Guggenheim is labeled "mechanical" by Bailyn, who contrasts it with the "thermodynamic" approach of Planck and the founders, who fully recognized the notion of heat transfer as an essential and fundamental presupposition to thermodynamics, without actually labelling it as a numbered law of thermodynamics. Since the time of Fowler and Guggenheim, who believed that the 1909 axiomatic formulation of Carathėodory was the most logically satisfactory, other influential axiomatic formulations of thermodynamics have appeared, some of which do not refer to a zeroth law of thermodynamics.
Sommerfeld
in 1951 gave the title the "Zeroth Law" to the statement "Equality of temperature is a condition for thermal equilibrium between two systems or between two parts of a single system"; he wrote that this title followed the suggestion of Fowler
, made when he was giving an account of a certain book. Sommerfeld's statement took the existence of temperature for granted, and used it to specify one of the characteristics of thermodynamic equilibrium. This is converse to many statements that are labeled as the zeroth law, which take thermal equilibrium for granted and use it to contribute to the concept of temperature. We may guess that Fowler had made his suggestion because the notion of temperature is in effect a presupposition of thermodynamics that earlier physicists had not felt needed explicit statement as a law of thermodynamics, and because the mood of his time, pursuing a "mechanical" axiomatic approach, wanted such an explicit statement.
Guggenheim in 1966 wrote "If two systems are both in thermal equilibrium with a third system then they are in thermal equilibrium with each other" as the zeroth law of thermodynamics, and followed it with the comment "In other words, systems in thermal equilibrium are said to have the same temperature." This ordinary language statement, although less precise than the statements of Planck and Tait mentioned above, conveys much of the essence of the zeroth law.
The statement of the zeroth law of thermodynamics by Serrin in 1977, though rather mathematically abstract, is more informative for empirical thermometry: "Zeroth Law - There exists a topological line which serves as a coordinate manifold of material behaviour. The points
which serves as a coordinate manifold of material behaviour. The points 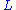 of the manifold
of the manifold  are called 'hotness levels', and
are called 'hotness levels', and  is called the 'universal hotness manifold'." To this information there needs to be added a sense of greater hotness; this sense can be had, independently of calorimetry
is called the 'universal hotness manifold'." To this information there needs to be added a sense of greater hotness; this sense can be had, independently of calorimetry
, of thermodynamics
, and of properties of particular materials, from Wien's displacement law of thermal radiation
: the temperature of a bath of thermal radiation
is proportional
, by a universal constant, to the frequency of the maximum of its frequency spectrum; this frequency is always positive, but can have values that tend to zero
.
Laws of thermodynamics
The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes...
is a generalization principle of thermal equilibrium
Thermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
among bodies, or thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
s, in contact.
The zeroth law states that if two systems are in thermal equilibrium with a third system, they are also in thermal equilibrium with each other.
Systems are said to be in thermal equilibrium if they do not actually exchange heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
, and, if they are not already connected by a conductor of heat or pathway for exchange of thermal radiation, would not do so if they were so connected. The law implies that thermal equilibrium between systems is a transitive relation
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, which affords the definition of an empirical physical parameter, called temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. The temperatures are equal for all systems in thermal equilibrium. The law permits the construction of a thermometer
Thermometer
Developed during the 16th and 17th centuries, a thermometer is a device that measures temperature or temperature gradient using a variety of different principles. A thermometer has two important elements: the temperature sensor Developed during the 16th and 17th centuries, a thermometer (from the...
to measure this property.
Zeroth law as equivalence relation
A system is said to be in thermal equilibriumThermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
when it experiences no net change in thermal energy. If A, B, and C are distinct thermodynamic system
Thermodynamic system
A thermodynamic system is a precisely defined macroscopic region of the universe, often called a physical system, that is studied using the principles of thermodynamics....
s, the zeroth
Zeroth
Zero-based numbering is numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday circumstances. Under zero-based numbering, the initial element is sometimes termed the zeroth element, rather than the first element; zeroth is a...
law of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
can be expressed as:
"If A and C are each in thermal equilibriumThermal equilibriumThermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
with B, A is also in equilibrium with C."
This statement asserts that thermal equilibrium is a Euclidean relation
Euclidean relation
In mathematics, Euclidean relations are a class of binary relations that satisfy a weakened form of transitivity that formalizes Euclid's "Common Notion 1" in The Elements: things which equal the same thing also equal one another.-Definition:...
between thermodynamic systems. If we also grant that all thermodynamic systems are in thermal equilibrium with themselves, then thermal equilibrium is also a reflexive relation
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
. Relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
that are both reflexive and Euclidean are equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s. One consequence of this reasoning is that thermal equilibrium is a transitive relation
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
ship: If A is in thermal equilibrium with B and B is in thermal equilibrium with C, then A is in thermal equilibrium with C. Another consequence is that the equilibrium relationship is symmetric: If A is in thermal equilibrium with B, then B is in thermal equilibrium with A. Thus we may say that two systems are in thermal equilibrium with each other, or that they are in mutual equilibrium. Implicitly assuming both reflexivity and symmetry, the zeroth law is therefore often expressed as:
"If two systems are in thermal equilibrium with a third system, then they are in thermal equilibrium with each other"
Again, implicitly assuming both reflexivity and symmetry, the zeroth law is occasionally expressed as the transitive relationship
"If A is in thermal equilibrium with B and if B is in thermal equilibrium with C, then A is in thermal equilibrium with C."
Thermal equilibrium between many systems
Many systems are said to be in equilibrium if the small, random exchanges (due to Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
or photon emissions, for example) between them do not lead to a net change in the total energy summed over all systems. A simple example illustrates why the zeroth law is necessary to complete the equilibrium description.
Consider N systems in adiabatic
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...
isolation from the rest of the universe, i.e. no heat exchange is possible outside of these N systems, all of which have a constant volume
Isochoric process
An isochoric process, also called a constant-volume process, an isovolumetric process, or an isometric process, is a thermodynamic process during which the volume of the closed system undergoing such a process remains constant...
and composition, and which can only exchange heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
with one another.
The combined First and Second Laws relate the fluctuations in total energy,
 , to the temperature of the ith system,
, to the temperature of the ith system, 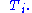 and the entropy
and the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
fluctuation in the ith system,
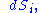 as follows:
as follows: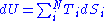 .
.The adiabatic
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...
isolation of the system from the remaining universe requires that the total sum of the entropy fluctuations vanishes, or:
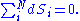
That is, entropy can only be exchanged between the N systems. This constraint can be used to rearrange the expression for the total energy fluctuation and obtain:
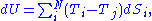
where
 is the temperature of any system j we may choose to single out among the N systems. Finally, equilibrium requires the total fluctuation in energy to vanish, in which case:
is the temperature of any system j we may choose to single out among the N systems. Finally, equilibrium requires the total fluctuation in energy to vanish, in which case: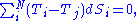
which can be thought of as the vanishing of the product of an antisymmetric matrix
 and a vector of entropy fluctuations
and a vector of entropy fluctuations 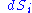 . In order for a non-trivial solution to exist,
. In order for a non-trivial solution to exist,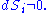
That is, the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix formed by
 must vanish for all choices of N. However, according to Jacobi's theorem, the determinant of a NxN antisymmetric matrix is always zero if N is odd, although for N even we find that all of the entries must vanish,
must vanish for all choices of N. However, according to Jacobi's theorem, the determinant of a NxN antisymmetric matrix is always zero if N is odd, although for N even we find that all of the entries must vanish,  , in order to obtain a vanishing determinant. Hence
, in order to obtain a vanishing determinant. Hence 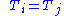 at equilibrium. This non-intuitive result means that an odd number of systems are always in equilibrium regardless of their temperatures and entropy fluctuations, while equality of temperatures is only required between an even number of systems to achieve equilibrium in the presence of entropy fluctuations.
at equilibrium. This non-intuitive result means that an odd number of systems are always in equilibrium regardless of their temperatures and entropy fluctuations, while equality of temperatures is only required between an even number of systems to achieve equilibrium in the presence of entropy fluctuations.The zeroth law solves this odd vs. even paradox, because it can readily be used to reduce an odd-numbered system to an even number by considering any three of the N systems and eliminating one by application of its principle, and hence reduce the problem to even N which subsequently leads to the same equilibrium condition that we expect in every case, i.e.,
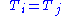 . The same result applies to fluctuations in any extensive quantity, such as volume (yielding the equal pressure condition), or fluctuations in mass (leading to equality of chemical potentials). Hence the zeroth law has implications for a great deal more than temperature alone. In general, we see that the zeroth law breaks a certain kind of asymmetry present in the First and Second Laws.
. The same result applies to fluctuations in any extensive quantity, such as volume (yielding the equal pressure condition), or fluctuations in mass (leading to equality of chemical potentials). Hence the zeroth law has implications for a great deal more than temperature alone. In general, we see that the zeroth law breaks a certain kind of asymmetry present in the First and Second Laws.Foundation of temperature
The zeroth law establishes thermal equilibrium as an equivalence relationship. An equivalence relationship on a set (such as the set of thermally equilibrated systems) divides that set into a collection of distinct subsets ("disjoint subsets") where any member of the set is a member of one and only one such subset. In the case of the zeroth law, these subsets consist of systems which are in mutual equilibrium. This partitioning allows any member of the subset to be uniquely "tagged" with a label identifying the subset to which it belongs. Although the labeling may be quite arbitrary, temperature is just such a labeling process which uses the real number system for tagging. The zeroth law justifies the use of suitable thermodynamic systems as thermometerThermometer
Developed during the 16th and 17th centuries, a thermometer is a device that measures temperature or temperature gradient using a variety of different principles. A thermometer has two important elements: the temperature sensor Developed during the 16th and 17th centuries, a thermometer (from the...
s to provide such a labeling, which yield any number of possible empirical temperature scales, and justifies the use of the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
to provide an absolute, or thermodynamic temperature
Thermodynamic temperature
Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
scale. Such temperature scales bring additional continuity and ordering (i.e., "hot" and "cold") properties to the concept of temperature.
In the space of thermodynamic parameters, zones of constant temperature form a surface, that provides a natural order of nearby surfaces. One may therefore construct a global temperature function that provides a continuous ordering of states. The dimensionality of a surface of constant temperature is one less than the number of thermodynamic parameters, thus, for an ideal gas described with three thermodynamic parameters P, V and n, it is a two-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al surface.
For example, if two systems of ideal gases are in equilibrium, then P1V1/N1 = P2V2/N2 where Pi is the pressure in the ith system, Vi is the volume, and Ni is the amount (in mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
s, or simply the number of atoms) of gas.
The surface PV/N = const defines surfaces of equal thermodynamic temperature, and one may label defining T so that PV/N = RT, where R is some constant. These systems can now be used as a thermometer to calibrate other systems. Such systems are known as "ideal gas thermometers".
History
Temperature has long been known as a quality of heat, for example, to GalileoGalileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
and to Newton. Carnot
Nicolas Léonard Sadi Carnot
Nicolas Léonard Sadi Carnot was a French military engineer who, in his 1824 Reflections on the Motive Power of Fire, gave the first successful theoretical account of heat engines, now known as the Carnot cycle, thereby laying the foundations of the second law of thermodynamics...
took it as a presupposition for his work. Thermometers may be described as empirical or absolute. Absolute thermometers are calibrated numerically by the thermodynamic absolute temperature scale
Thermodynamic temperature
Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
. It was not until the middle of the nineteenth century that absolute thermodynamic temperature was recognized, long after the recognition of empirical thermometry.
Empirical thermometry recognizes hotness as a fundamental character of temperature and thermometers. Empirical thermometers are not in general necessarily in exact agreement with each other or with absolute thermometers as to their numerical scale readings, but to qualify as thermometers at all they must agree with absolute thermometers and with each other in the following way: given any two bodies isolated in their separate respective thermodynamic equilibrium states, all thermometers agree as to which of the two has the higher temperature, or that the two have equal temperatures. For any two empirical thermometers, this does not require that the relation between their numerical scale readings be linear, but it does require that relation to be strictly monotonic.
Truesdell
Clifford Truesdell
Clifford Ambrose Truesdell III was an American mathematician, natural philosopher, historian of science, and polemicist.-Life:...
reports that Rankine
William John Macquorn Rankine
William John Macquorn Rankine was a Scottish civil engineer, physicist and mathematician. He was a founding contributor, with Rudolf Clausius and William Thomson , to the science of thermodynamics....
wrote in 1853:
-
-
-
-
-
-
-
-
-
- Definition of equal temperatures.
-
-
-
-
-
-
-
-
- Two portions of matter are said to have equal temperatures, when neither tends to communicate heat to the other.
Discussing the concept of temperature, James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
in 1872 wrote: "If when two bodies are placed in thermal communication, one of the two bodies loses heat, and the other gains heat, that body which gives out heat is said to have a higher temperature than that which receives heat from it." He drew the corollary "If when two bodies are placed in thermal communication neither of them loses or gains heat, the two bodies are said to have equal temperatures or the same temperature. The two bodies are then said to be in thermal equilibrium."
Further, Maxwell stated, as the "Law of equal temperatures" the following triviality: "Bodies whose temperatures are equal to that of the same body have themselves equal temperatures". Maxwell then offered an argument that this statement was "not a truism". Later in the same text, Maxwell wrote: "Hence the result of the conduction and radiation of heat from one part of a system to another is to diminish the entropy of the system, or the energy, available as work, which can be obtained from the system." This statement was surrounded in Maxwell's text by several others like it that show that it was no slip of the pen. In the same textbook, Maxwell wrote that he was following Tait in re-defining the word entropy that had been introduced by Clausius. In contrast with what Maxwell wrote then, Tait had changed his mind by 1884 when in his text he accepted Clausius's original definition of entropy.
Subsequent writers made statements like Maxwell's. Tait in 1884 wrote "if A is at the same temperature as B and also at the same temperature as C — no transfer of heat takes place between B and C, whatever be these bodies." A similar statement was made by Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
in 1897, not labeled as a law but as an important proposition: "If a body, A, be in thermal equilibrium with two other bodies, B and C, then B and C are in thermal equilibrium with one another." Planck repeated this important proposition in the seventh edition of his treatise in 1922.
The title "zeroth law of thermodynamics" began to appear in textbooks to refer to statements of this kind, though now stripped of their explicit reference to heat; their implicit dependence on the notion of heat could not be removed because they rely on the concept of thermal equilibrium which in turn relies on the concept of transfer of heat by conduction or radiation, the presence or absence of which must be empirically recognizable in order to make the concept of thermal equilibrium empirically recognizable. An early example is in the textbook of statistical thermodynamics of Fowler and Guggenheim (1939/1965). Their focus of interest in that book was homogeneous systems (page 1), which they termed 'assemblies'. They dealt with assemblies that were either completely homogeneous or that could be divided into homogeneous parts, called phases (page 58). For their macroscopic thermodynamic account of phenomena, they started by accepting, on empirical physical grounds, the presupposed notions of thermal insulation, thermal contact, and thermal equilibrium (page 56). They emphasized that these notions "can be defined without any reference to temperature" (page 56). Moreover, they gave at this stage of their development of their theory no hint of the notion of heat transfer. On page 56, they wrote:
-
- ...we introduce the postulate: If two assemblies are each in thermal equilibrium with a third assembly, they are in thermal equilibrium with each other.
They then proposed that "it may be shown to follow that the condition for thermal equilibrium between several assemblies is the equality of a certain single-valued function of the thermodynamics states of the assemblies, which may be called the temperature t, any one of the assemblies being used as a "thermometer" reading the temperature t on a suitable scale. This postulate of the "Existence of temperature" could with advantage be known as the zeroth law of thermodynamics" (page 56). They did not there state any reason why such a function should have values in a scale consisting of a continuous succession of numbers or that it should have anything to do with heat. Their thinking was apparently conditioned by their asserted belief that "The most logically satisfactory formulation [of homogeneous system macroscopic thermodynamics] is undoubtedly that of Carathéodory" (page 56). Though they thus apparently professed concern for logicality, they had no apparent compunction about immediately assuming, without apparent justification, that their postulated "temperatures" should exist on a numerical scale, provided for example by "the measured volume of a constant quantity of any chosen substance at constant pressure" (page 56). No worries about pesky but relevant physical realities such as the anomalous behaviour of water that concerned the nineteenth century thermodynamicists, because around 4 C it does not provide a valid empirical temperature. No mention that it would therefore be safer to refer to a permanent gas as a thermometric material. The approach of Fowler and Guggenheim is labeled "mechanical" by Bailyn, who contrasts it with the "thermodynamic" approach of Planck and the founders, who fully recognized the notion of heat transfer as an essential and fundamental presupposition to thermodynamics, without actually labelling it as a numbered law of thermodynamics. Since the time of Fowler and Guggenheim, who believed that the 1909 axiomatic formulation of Carathėodory was the most logically satisfactory, other influential axiomatic formulations of thermodynamics have appeared, some of which do not refer to a zeroth law of thermodynamics.
Sommerfeld
Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
in 1951 gave the title the "Zeroth Law" to the statement "Equality of temperature is a condition for thermal equilibrium between two systems or between two parts of a single system"; he wrote that this title followed the suggestion of Fowler
Ralph H. Fowler
Sir Ralph Howard Fowler OBE FRS was a British physicist and astronomer.-Education:Fowler was initially educated at home but then attended Evans' preparatory school at Horris Hill and Winchester College...
, made when he was giving an account of a certain book. Sommerfeld's statement took the existence of temperature for granted, and used it to specify one of the characteristics of thermodynamic equilibrium. This is converse to many statements that are labeled as the zeroth law, which take thermal equilibrium for granted and use it to contribute to the concept of temperature. We may guess that Fowler had made his suggestion because the notion of temperature is in effect a presupposition of thermodynamics that earlier physicists had not felt needed explicit statement as a law of thermodynamics, and because the mood of his time, pursuing a "mechanical" axiomatic approach, wanted such an explicit statement.
Guggenheim in 1966 wrote "If two systems are both in thermal equilibrium with a third system then they are in thermal equilibrium with each other" as the zeroth law of thermodynamics, and followed it with the comment "In other words, systems in thermal equilibrium are said to have the same temperature." This ordinary language statement, although less precise than the statements of Planck and Tait mentioned above, conveys much of the essence of the zeroth law.
The statement of the zeroth law of thermodynamics by Serrin in 1977, though rather mathematically abstract, is more informative for empirical thermometry: "Zeroth Law - There exists a topological line
 which serves as a coordinate manifold of material behaviour. The points
which serves as a coordinate manifold of material behaviour. The points 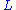 of the manifold
of the manifold  are called 'hotness levels', and
are called 'hotness levels', and  is called the 'universal hotness manifold'." To this information there needs to be added a sense of greater hotness; this sense can be had, independently of calorimetry
is called the 'universal hotness manifold'." To this information there needs to be added a sense of greater hotness; this sense can be had, independently of calorimetryCalorimetry
Calorimetry is the science of measuring the heat of chemical reactions or physical changes. Calorimetry is performed with a calorimeter. The word calorimetry is derived from the Latin word calor, meaning heat...
, of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, and of properties of particular materials, from Wien's displacement law of thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
: the temperature of a bath of thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
is proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
, by a universal constant, to the frequency of the maximum of its frequency spectrum; this frequency is always positive, but can have values that tend to zero
Third law of thermodynamics
The third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:...
.

