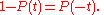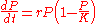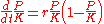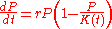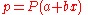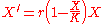Logistic function
Encyclopedia
Pierre François Verhulst
Pierre François Verhulst was a mathematician and a doctor in number theory from the University of Ghent in 1825...
who studied it in relation to population growth. It can model the "S-shaped" curve (abbreviated S-curve) of growth of some population P. The initial stage of growth is approximately exponential
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
; then, as saturation begins, the growth slows, and at maturity, growth stops.
A simple logistic function may be defined by the formula
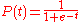
where the variable P might be considered to denote a population, where e is Euler's number and the variable t might be thought of as time. For values of t in the range of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s from −∞ to +∞, the S-curve shown is obtained. In practice, due to the nature of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
e−t, it is sufficient to compute t over a small range of real numbers such as [−6, +6].
The logistic function finds applications in a range of fields, including artificial neural network
Artificial neural network
An artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...
s, biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
, biomathematics, demography
Demography
Demography is the statistical study of human population. It can be a very general science that can be applied to any kind of dynamic human population, that is, one that changes over time or space...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, mathematical psychology
Mathematical psychology
Mathematical psychology is an approach to psychological research that is based on mathematical modeling of perceptual, cognitive and motor processes, and on the establishment of law-like rules that relate quantifiable stimulus characteristics with quantifiable behavior...
, probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, sociology
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, political science
Political science
Political Science is a social science discipline concerned with the study of the state, government and politics. Aristotle defined it as the study of the state. It deals extensively with the theory and practice of politics, and the analysis of political systems and political behavior...
, and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
. It has an easily calculated derivative:
It also has the property that
In other words, the function P − 1/2 is odd.
Logistic differential equation
The logistic function is the solution of the simple first-order non-linear differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

where P is a variable with respect to time t and with boundary condition P(0) = 1/2. This equation is the continuous version of the logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
.
The qualitative behavior is easily understood in terms of the phase line
Phase line (mathematics)
In mathematics, a phase line is a diagram that shows the qualitative behaviour of an autonomous ordinary differential equation in a single variable, dy/dt = ƒ...
: the derivative is 0 at P = 0 or 1 and the derivative is positive for P between 0 and 1, and negative for P above 1 or less than 0 (though negative populations do not generally accord with a physical model). This yields an unstable equilibrium at 0, and a stable equilibrium at 1, and thus for any value of P greater than 0 and less than 1, P grows to 1.
One may readily find the (symbolic) solution to be

Choosing the constant of integration ec = 1 gives the other well-known form of the definition of the logistic curve
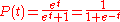
More quantitatively, as can be seen from the analytical solution, the logistic curve shows early exponential growth
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
for negative t, which slows to linear growth of slope 1/4 near t = 0, then approaches y = 1 with an exponentially decaying gap.
The logistic function is the inverse of the natural logit
Logit
The logit function is the inverse of the sigmoidal "logistic" function used in mathematics, especially in statistics.Log-odds and logit are synonyms.-Definition:The logit of a number p between 0 and 1 is given by the formula:...
function and so can be used to convert the logarithm of odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
into a probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
; the conversion from the log-likelihood ratio of two alternatives also takes the form of a logistic curve.
The logistic sigmoid function is related to the hyperbolic tangent, A.p. by
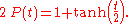
In ecology: modeling population growth

Population growth
Population growth is the change in a population over time, and can be quantified as the change in the number of individuals of any species in a population using "per unit time" for measurement....
, originally due to Pierre-François Verhulst
Pierre François Verhulst
Pierre François Verhulst was a mathematician and a doctor in number theory from the University of Ghent in 1825...
in 1838, where the rate of reproduction is proportional to both the existing population and the amount of available resources, all else being equal. The Verhulst equation was published after Verhulst had read Thomas Malthus
Thomas Malthus
The Reverend Thomas Robert Malthus FRS was an English scholar, influential in political economy and demography. Malthus popularized the economic theory of rent....
' An Essay on the Principle of Population
An Essay on the Principle of Population
The book An Essay on the Principle of Population was first published anonymously in 1798 through J. Johnson . The author was soon identified as The Reverend Thomas Robert Malthus. While it was not the first book on population, it has been acknowledged as the most influential work of its era...
. Verhulst derived his logistic equation to describe the self-limiting growth of a biological
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
population. The equation is also sometimes called the Verhulst-Pearl equation following its rediscovery in 1920. Alfred J. Lotka
Alfred J. Lotka
Alfred James Lotka was a US mathematician, physical chemist, and statistician, famous for his work in population dynamics and energetics. An American biophysicist best known for his proposal of the predator-prey model, developed simultaneously but independently of Vito Volterra...
derived the equation again in 1925, calling it the law of population growth.
Letting P represent population size (N is often used in ecology instead) and t represent time, this model is formalized by the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
:
where the constant r defines the growth rate and K is the carrying capacity
Carrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
.
In the equation, the early, unimpeded growth rate is modeled by the first term +rP. The value of the rate r represents the proportional increase of the population P in one unit of time. Later, as the population grows, the second term, which multiplied out is −rP2/K, becomes larger than the first as some members of the population P interfere with each other by competing for some critical resource, such as food or living space. This antagonistic effect is called the bottleneck, and is modeled by the value of the parameter K. The competition diminishes the combined growth rate, until the value of P ceases to grow (this is called maturity of the population).
Dividing both sides of the equation by K gives
Now setting
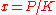 gives the differential equation
gives the differential equationFor
 we have the particular case with which we started.
we have the particular case with which we started.In ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
, species
Species
In biology, a species is one of the basic units of biological classification and a taxonomic rank. A species is often defined as a group of organisms capable of interbreeding and producing fertile offspring. While in many cases this definition is adequate, more precise or differing measures are...
are sometimes referred to as r-strategist or K-strategist depending upon the selective
Natural selection
Natural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....
processes that have shaped their life history
Biological life cycle
A life cycle is a period involving all different generations of a species succeeding each other through means of reproduction, whether through asexual reproduction or sexual reproduction...
strategies. The solution to the equation (with
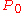 being the initial population) is
being the initial population) is
where
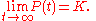
Which is to say that K is the limiting value of P: the highest value that the population can reach given infinite time (or come close to reaching in finite time). It is important to stress that the carrying capacity is asymptotically reached independently of the initial value P(0) > 0, also in case that P(0) > K.
Time-varying carrying capacity
Since the environmental conditions influence the carrying capacity, as a consequence it can be time-varying: K(t) > 0, leading to the following mathematical model:A particularly important case is that of carrying capacity that varies periodically with period T:
It can be shown that in such a case, independently from the initial value P(0) > 0, P(t) will tend to a unique periodic solution P*(t), whose period is T.
A typical value of T is one year: in such case K(t) reflects periodical variations of weather conditions.
Another interesting generalization is to consider that the carrying capacity K(t) is a function of the population
at an earlier time, capturing a delay in the way population modifies its environment. This leads to a logistic
delay equation, which has a very rich behavior, with bistability in some parameter range, as well as a monotonic decay to zero, smooth exponential growth, punctuated unlimited growth (i.e., multiple S-shapes), punctuated growth or alternation to a stationary level, oscillatory approach to a stationary level, sustainable oscillations, finite-time singularities as well as finite-time death.
In neural networks
Logistic functions are often used in neural networkNeural network
The term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
s to introduce nonlinearity
Nonlinearity
In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...
in the model and/or to clamp signals to within a specified range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
. A popular neural net element
Artificial neuron
An artificial neuron is a mathematical function conceived as a crude model, or abstraction of biological neurons. Artificial neurons are the constitutive units in an artificial neural network...
computes a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of its input signals, and applies a bounded logistic function to the result; this model can be seen as a "smoothed" variant of the classical threshold neuron
Perceptron
The perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
.
A common choice for the activation or "squashing" functions, used to clip for large magnitudes to keep the response of the neural network bounded is

which we recognize to be of the form of the logistic function.
These relationships result in simplified implementations of artificial neural network
Artificial neural network
An artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...
s with artificial neuron
Artificial neuron
An artificial neuron is a mathematical function conceived as a crude model, or abstraction of biological neurons. Artificial neurons are the constitutive units in an artificial neural network...
s. Practitioners caution that sigmoidal functions which are antisymmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
about the origin (e.g. the hyperbolic tangent) lead to faster convergence when training networks with backpropagation
Backpropagation
Backpropagation is a common method of teaching artificial neural networks how to perform a given task. Arthur E. Bryson and Yu-Chi Ho described it as a multi-stage dynamic system optimization method in 1969 . It wasn't until 1974 and later, when applied in the context of neural networks and...
.
In statistics
Logistic functions are used in several roles in statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
. Firstly, they are the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the logistic family of distributions. Secondly they are used in logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
to model how the probability p of an event may be affected by one or more explanatory variables: an example would be to have the model
where x is the explanatory variable and a and b are model parameters to be fitted.
An important application of the logistic function is in the Rasch model
Rasch model
Rasch models are used for analysing data from assessments to measure variables such as abilities, attitudes, and personality traits. For example, they may be used to estimate a student's reading ability from answers to questions on a reading assessment, or the extremity of a person's attitude to...
, used in item response theory
Item response theory
In psychometrics, item response theory also known as latent trait theory, strong true score theory, or modern mental test theory, is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is based...
. In particular, the Rasch model forms a basis for maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimation of the locations of objects or persons on a continuum
Continuum (theory)
Continuum theories or models explain variation as involving a gradual quantitative transition without abrupt changes or discontinuities. It can be contrasted with 'categorical' models which propose qualitatively different states.-In physics:...
, based on collections of categorical data, for example the abilities of persons on a continuum based on responses that have been categorized as correct and incorrect.
In medicine: modeling of growth of tumors
Another application of logistic curve is in medicine, where the logistic differential equation is used to model the growth of tumors. This application can be considered an extension of the above mentioned use in the framework of ecology. Denoting with X(t) the size of the tumor at time t, its dynamics are governed by:which is of the type:

where F(X) is the proliferation rate of the tumor.
If a chemotherapy is started with a log-kill effect, the equation may be revised to be
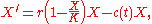
where c(t) is the therapy-induced death rate. In the idealized case of very long therapy, c(t) can be modeled as a periodic function (of period T) or (in case of continuous infusion therapy) as a constant function, and one has that
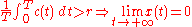
i.e. if the average therapy-induced death rate is greater than the baseline proliferation rate then there is the eradication of the disease. Of course, this is an over-simplified model of both the growth and the therapy (e.g. it does not take into account the phenomenon of clonal resistance).
In chemistry: reaction models
The concentration of reactants and products in autocatalytic reactionsAutocatalysis
A single chemical reaction is said to have undergone autocatalysis, or be autocatalytic, if the reaction product itself is the catalyst for that reaction....
follow the logistic function.
In physics: Fermi distribution
The logistic function determines the statistical distribution of fermions over the energy states of a system in thermal equilibrium. In particular, it is the distribution of the probabilities that each possible energy level is occupied by a fermion, according to Fermi–Dirac statistics.In linguistics: language change
In linguistics, the logistic function can be used to model language changeLanguage change
Language change is the phenomenon whereby phonetic, morphological, semantic, syntactic, and other features of language vary over time. The effect on language over time is known as diachronic change. Two linguistic disciplines in particular concern themselves with studying language change:...
: an innovation that is at first marginal begins to spread more quickly with time, and then more slowly as it becomes more universally adopted.
In economics: diffusion of innovations
The logistic function can be used to illustrate the progress of the diffusion of an innovationDiffusion of innovations
Diffusion of Innovations is a theory that seeks to explain how, why, and at what rate new ideas and technology spread through cultures. Everett Rogers, a professor of rural sociology, popularized the theory in his 1962 book Diffusion of Innovations...
through its life cycle. This method was used in papers by several researchers at the International Institute of Applied Systems Analysis (IIASA
IIASA
The International Institute for Applied Systems Analysis is an international research organization located in Laxenburg, near Vienna, in Austria. IIASA conducts interdisciplinary scientific studies on environmental, economic, technological and social issues in the context of human dimensions of...
). These papers deal with the diffusion of various innovations, infrastructures and energy source substitutions and the role of work in the economy as well as with the long economic cycle. Long economic cycles were investigated by Robert Ayres (1989). Cesare Marchetti published on long economic cycles
Kondratiev wave
Kondratiev waves are described as sinusoidal-like cycles in the modern capitalist world economy...
and on diffusion of innovations. Arnulf Grübler’s book (1990) gives a detailed account of the diffusion of infrastructures including canals, railroads, highways and airlines , showing that their diffusion followed logistic shaped curves.
Carlota Perez used a logistic curve to illustrate the long (Kondratiev
Kondratiev wave
Kondratiev waves are described as sinusoidal-like cycles in the modern capitalist world economy...
) business cycle with the following labels: beginning of a technological era as irruption, the ascent as frenzy, the rapid build out as synergy and the completion as maturity.
Double logistic function
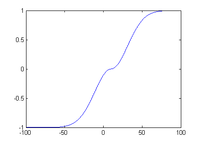
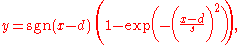
where d is its centre and s is the steepness factor. Here "sgn" represents the sign function
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
.
It is based on the Gaussian curve and graphically it is similar to two identical logistic sigmoids bonded together at the point x = d.
One of its applications is non-linear normalization
Normalization (statistics)
In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
of a sample, as it has the property of eliminating outlier
Outlier
In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....
s.
External links
- L.J. Linacre, Why logistic ogive and not autocatalytic curve?, accessed 2009-09-12.
- http://luna.cas.usf.edu/~mbrannic/files/regression/Logistic.html
- Modeling Market Adoption in Excel with a simplified s-curve
- Online experiments with JSXGraph