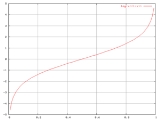
Logit
Encyclopedia
The logit function is the inverse
of the sigmoidal
"logistic" function
used in mathematics
, especially in statistics
.
Log-odds and logit are synonyms.

The base of the logarithm
function used is of little importance in the present article, as long as it is greater than 1, but the natural logarithm
with base e
is the one most often used.
The "logistic" function
of any number is given by the inverse-logit:
is given by the inverse-logit:

If p is a probability
then p/(1 − p) is the corresponding odds
, and the logit of the probability is the logarithm of the odds; similarly the difference between the logits of two probabilities is the logarithm of the odds ratio
(R), thus providing a shorthand for writing the correct combination of odds ratios only by adding and subtracting
:

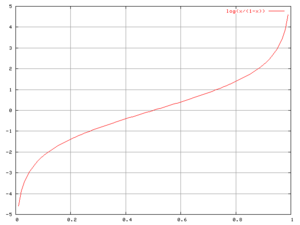
in 1944, who coined the term. The term was borrowed by analogy from the very similar probit
model developed by Chester Ittner Bliss
in 1934. G. A. Barnard in 1949 coined the commonly used term log-odds; the log-odds of an event is the logit of the probability of the event.
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of the sigmoidal
Sigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
"logistic" function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
used in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in statistics
Data transformation (statistics)
In statistics, data transformation refers to the application of a deterministic mathematical function to each point in a data set — that is, each data point zi is replaced with the transformed value yi = f, where f is a function...
.
Log-odds and logit are synonyms.
Definition
The logit of a number p between 0 and 1 is given by the formula:
The base of the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
function used is of little importance in the present article, as long as it is greater than 1, but the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
with base e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
is the one most often used.
The "logistic" function
Logistic function
A logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
of any number
 is given by the inverse-logit:
is given by the inverse-logit:
If p is a probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
then p/(1 − p) is the corresponding odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
, and the logit of the probability is the logarithm of the odds; similarly the difference between the logits of two probabilities is the logarithm of the odds ratio
Odds ratio
The odds ratio is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression...
(R), thus providing a shorthand for writing the correct combination of odds ratios only by adding and subtracting
Additive function
In mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
:


History
The logit model was introduced by Joseph BerksonJoseph Berkson
Joseph Berkson was trained as a physicist , physician , and statistician . In 1950, as Head of the Division of Biometry and Medical Statistics of the Mayo Clinic, Rochester, Minnesota, Berkson wrote a key paper entitled Are there two regressions?...
in 1944, who coined the term. The term was borrowed by analogy from the very similar probit
Probit
In probability theory and statistics, the probit function is the inverse cumulative distribution function , or quantile function associated with the standard normal distribution...
model developed by Chester Ittner Bliss
Chester Ittner Bliss
Chester Ittner Bliss was primarily a biologist, who is best known for his contributions to statistics. He was born in Springfield, Ohio in 1899 and died in 1979.-Academic qualifications:*Bachelor of Arts in Entomology from Ohio State University, 1921...
in 1934. G. A. Barnard in 1949 coined the commonly used term log-odds; the log-odds of an event is the logit of the probability of the event.
Uses and properties
- The logit in logistic regressionLogistic regressionIn statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
is a special case of a link function in a generalized linear modelGeneralized linear modelIn statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
: it is the canonical link function for the binomial distribution. - The logit function is the negative of the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the binary entropy function. - The logit is also central to the probabilistic Rasch modelRasch modelRasch models are used for analysing data from assessments to measure variables such as abilities, attitudes, and personality traits. For example, they may be used to estimate a student's reading ability from answers to questions on a reading assessment, or the extremity of a person's attitude to...
for measurementMeasurementMeasurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
, which has applications in psychological and educational assessment, among other areas. - The inverse-logit function is also sometimes referred to as the expit function.
See also
- Discrete choiceDiscrete choiceIn economics, discrete choice problems involve choices between two or more discrete alternatives, such as entering or not entering the labor market, or choosing between modes of transport. Such choices contrast with standard consumption models in which the quantity of each good consumed is assumed...
on binary logit, multinomial logit, conditional logit, nested logit, mixed logit, exploded logit, and ordered logit - Limited dependent variableLimited dependent variableA limited dependent variable is a variable whose range ofpossible values is "restricted in some important way." In econometrics, the term is often used whenestimation of the relationship between the limited dependent variable...
- Daniel McFaddenDaniel McFaddenDaniel Little McFadden is an econometrician who shared the 2000 Nobel Memorial Prize in Economic Sciences with James Heckman ; McFadden's share of the prize was "for his development of theory and methods for analyzing discrete choice". He was the E. Morris Cox Professor of Economics at the...
, a Nobel Prize winner for development of a particular logit model used in economic - Logit analysis in marketing
- PerceptronPerceptronThe perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
- ProbitProbitIn probability theory and statistics, the probit function is the inverse cumulative distribution function , or quantile function associated with the standard normal distribution...
another function with the same domain and range as the logit - Ridit scoringRidit scoringIn econometrics, ridit scoring is a statistical method used to analyze ordered qualitative measurements.The tools of ridit analysis were developed and first applied by Bross, who coined the term "ridit" by analogy with other statistical transformations such as probit and logit.-Choosing a reference...
- Data transformation (statistics)Data transformation (statistics)In statistics, data transformation refers to the application of a deterministic mathematical function to each point in a data set — that is, each data point zi is replaced with the transformed value yi = f, where f is a function...

