List of topics named after Leonhard Euler

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

and physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, there is a large number of topics named in honor of Leonhard Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

, many of which include their own unique function, equation, formula, identity, number (single or sequence), or other mathematical entity. Unfortunately, many of these entities have been given simple and ambiguous names such as Euler's function, Euler's equation, and Euler's formula.

Euler's work touched upon so many fields that he is often the earliest written reference on a given matter. Physicists and mathematicians sometimes jest that, in an effort to avoid naming everything after Euler, discoveries and theorems are named after the "first person after Euler to discover it".

General "Euler-" mathematical topics

Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...

defining a rotation in space.
Euler approximation – (see Euler method)
Euler brick
Euler brick
In mathematics, an Euler brick, named after Leonhard Euler, is a cuboid whose edges and face diagonals all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime.- Properties :...
Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

and topological graph theory
Topological graph theory
In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....

, and the corresponding Euler's formula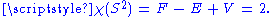
Euler circle
Nine-point circle
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
Eulerian circuit – (see Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

)
Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
Euler's constant – (see Euler–Mascheroni constant) (not to be confused with Euler's number)
Euler cycle – (see Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

)
Euler's criterion
Euler's criterion
In mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...

– quadratic residues modulo primes
Euler derivative (as opposed to Lagrangian derivative)
Euler diagram
Euler diagram
An Euler diagram is a diagrammatic means of representing sets and their relationships. The first use of "Eulerian circles" is commonly attributed to Swiss mathematician Leonhard Euler . They are closely related to Venn diagrams....

– likely more widely (though incorrectly) known as Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...

(which has more restrictions)
Euler's disk
Euler's disk
Euler's Disk is a scientific educational toy, used to illustrate and study the dynamic system of a spinning disk on a flat surface , and has been the subject of a number of scientific papers. This phenomenon has been studied since Leonard Euler in the 18th century, hence the name.It is manufactured...

– a circular disk that spins, without slipping, on a surface
Eulerian graph – (see Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

)
The Euler integrals of the first and second kind, namely the beta function and gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...

.
Euler's line
Euler's line
In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral; it passes through several important points determined from the triangle...

– relation between triangle center
Triangle center
In geometry a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles. For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of...

s
Euler–Mascheroni constant or Euler's constant γ ≈ 0.577216
Euler's number, e, the base of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

.
Euler operator
Euler operator
In mathematics, Euler operators are a small set of functions to create polygon meshes. They are closed and sufficient on the set of meshes, and they are invertible.- Purpose :...

– set of functions to create polygon mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...

es
Euler parameters – (see Euler–Rodrigues parameters)
Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

, a path through a graph that takes each edge once.
Euler polynomials
Euler pseudoprime
Euler pseudoprime
In arithmetic, an odd composite integer n is called an Euler pseudoprime to base a, if a and n are coprime, and....
Euler–Rodrigues parameters – concerns Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

s and quaternions
Euler's rule
Euler's rule
Euler's rule, named after Leonhard Euler, is a generalization of Thâbit ibn Kurrah rule for finding amicable numbers. If a = 2m× − 1, b = 2n× − 1, and c = 2n+m×2 − 1 are all prime, for integers 0 Euler's rule, named after Leonhard Euler, is a generalization of Thâbit ibn Kurrah rule for finding...

– finding amicable numbers
Euler spline – composed of classical Euler polynomial arcs (cred. to Schoenberg, 1973 – PDF)
Euler squares, usually called Graeco-Latin square
Graeco-Latin square
In mathematics, a Graeco-Latin square or Euler square or orthogonal Latin squares of order n over two sets S and T, each consisting of n symbols, is an n×n arrangement of cells, each cell containing an ordered pair , where s is in S and t is in T, such that every row and every column contains...

s.
Euler summation
Euler summation
Euler summation is a summability method for convergent and divergent series. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series....
Euler system
Euler system
In mathematics, an Euler system is collection of compatible elements of Galois cohomology groups indexed by fields. They were introduced by in his work on Heegner points on modular elliptic curves, which was motivated by his earlier paper and the work of...

, a collection of cohomology classes.
Euler's three-body problem
Euler's three-body problem
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...

See also: Other things named after Euler

Euler—conjectures

Euler's conjecture (Waring's problem)
Euler's sum of powers conjecture

(Also see Euler's conjecture.)

Euler—equations

Euler's equation – usually refers to Euler's equations (rigid body dynamics), Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...

, Euler's homogeneous function theorem, or Euler's identity
Euler equations (fluid dynamics) in fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

.
Euler's equations (rigid body dynamics), concerning the rotations of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...

.
Euler–Bernoulli beam equation, concerning the elasticity of structural beams.
Euler–Cauchy equation (or Euler equation), a second-order linear differential equation
Euler–Lagrange equation (in regard to minimization problems in calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...

)
Euler–Lotka equation
Euler–Lotka equation
The field of mathematical demography was largely developed by Alfred J. Lotka in the early 20th century, building on the earlier work of Leonhard Euler...

(mathematical demography)
Euler–Poisson–Darboux equation
Euler–Poisson–Darboux equation
The Euler–Poisson–Darboux equation is the partial differential equationThis equation is named for Siméon Poisson, Leonhard Euler, and Gaston Darboux. This equation plays important role in solving the classical wave equation....
Euler's pump and turbine equation
Euler–Tricomi equation – concerns transonic flow
Euler transform used to accelerate the convergence of an alternating series and is also frequently applied to the hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...

Euler—formulae

Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...

e^ix = cos x + i sin x in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

.
Euler's formula for planar graphs: v − e + f = 2
Euler's formula for the critical load of a column:
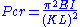
Euler's continued fraction formula
Euler's continued fraction formula
In the analytic theory of continued fractions, Euler's continued fraction formula is an identity connecting a certain very general infinite series with an infinite continued fraction. First published in 1748, it was at first regarded as a simple identity connecting a finite sum with a finite...
Euler product formula
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...

– for the Riemann zeta function.
Euler's summation formula, a theorem about integrals.
Euler–Maclaurin formula – relation between integrals and sums
Euler–Rodrigues formulas – concerns Euler–Rodrigues parameters and 3D rotation matrices

Euler—functions

The Euler function, a modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...

that is a prototypical q-series.
Euler's homogeneous function theorem
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...

(or Euler phi (φ) function) in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, counting the number of coprime integers less than an integer.
Euler hypergeometric integral

Euler—identities

Euler's identity e^iπ + 1 = 0.
Euler's four-square identity
Euler's four-square identity
In mathematics, Euler's four-square identity says that the product of two numbers, each of which being a sum of four squares, is itself a sum of four squares. Specifically:=\,...

, which shows that the product of two sums of four squares can itself be expressed as the sum of four squares.
Euler's identity may also refer to the pentagonal number theorem.

Euler—numbers

Euler's number
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...

, e ≈ 2.71828, the base of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

, also known as Napier's constant.
Euler's idoneal numbers
Euler numbers are an integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...

.
Eulerian number
Eulerian number
In combinatorics the Eulerian number A, is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element...

s are another integer sequence.
Euler number (physics)
Euler number (physics)
The Euler number is a dimensionless number used in fluid flow calculations. It expresses the relationship between a local pressure drop e.g. over a restriction and the kinetic energy per volume, and is used to characterize losses in the flow, where a perfect frictionless flow corresponds to an...

, the cavitation number in fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

.
Euler number (topology) – now, Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
Lucky numbers of Euler
Lucky numbers of Euler
Euler's "lucky" numbers are positive integers n such that m2 − m + n is a prime number for m = 0, …, n − 1.Leonhard Euler published the polynomial x2 − x + 41 which produces prime numbers for all integer values of x from 0 to 40. Obviously, when x is equal to 41, the value cannot be prime...
Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
Eulerian integers are the numbers of form a+bω where ω is a complex cube root of 1.

Euler—theorems

Euler's homogeneous function theorem, a theorem about homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...

s.
Euler's infinite tetration theorem
Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
Euler's theorem (differential geometry)
Euler's theorem (differential geometry)
In the mathematical field of differential geometry, Euler's theorem is a result on the curvature of curves on a surface. The theorem establishes the existence of principal curvatures and associated principal directions which give the directions in which the surface curves the most and the least...

on the existence of the principal curvatures of a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

and orthogonality of the associated principal directions.
Euler's theorem in geometry
Euler's theorem in geometry
In geometry, Euler's theorem, named after Leonhard Euler, states that the distance d between the circumcentre and incentre of a triangle can be expressed as d^2=R \,...

, relating the circumcircle and incircle of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

.
Euclid–Euler theorem
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
Euler–Fermat theorem, that a^φ(m) ≡ 1 (mod m) whenever a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...

to m, and φ is the totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...

.

Euler's adding-up theorem in economics

Euler—laws

Euler's first law, the linear momentum of a body is equal to the product of the mass of the body and the velocity of its center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...

.
Euler's second law, the sum of the external moments
Moment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...

about a point is equal to the rate of change of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...

about that point.

Other things named after Euler

2002 Euler
2002 Euler
2002 Euler is an asteroid named after the Swiss mathematician and physicist Leonhard Euler. The asteroid was discovered on August 29, 1973, by Tamara Mikhailovna Smirnova....

(an asteroid)
Euler–Fokker genus
Euler Medal
Euler Medal
The Euler Medal, named after the 18th century mathematician Leonhard Euler, is an honor awarded annually by the Institute of Combinatorics and its Applications to a member with a distinguished lifetime contribution to combinatorial research who are still active in research.-Laureates:* 2008: Gabor...

, a prize for research in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
Euler programming language
Euler programming language
Euler is a programming language created by Niklaus Wirth and Helmut Weber, conceived as an extension and generalization of ALGOL 60. The designers' goal was to create a language:* which was simpler, and yet more flexible, than ALGOL 60...
Euler (software)
AMS Euler
AMS Euler
AMS Euler is an upright cursive typeface, commissioned by the American Mathematical Society and designed and created by Hermann Zapf with the assistance of Donald Knuth. It tries to emulate a mathematician's style of handwriting mathematical entities on a blackboard, which is upright rather than...

typeface
Project Euler
Project Euler
Project Euler is a website dedicated to a series of computational problems intended to be solved with computer programs. The project attracts adults and students interested in mathematics and computer programming. , it includes 351 problems of varying difficulty, each solvable in less than a...

Derivatives and integrals

Euler approximation – (see Euler's method)
Euler derivative (as opposed to Lagrangian derivative)
The Euler integrals of the first and second kind, namely the beta function and gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...

.
The Euler method, a method for finding numerical solutions of differential equations
- Semi-implicit Euler method
  Semi-implicit Euler method
  In mathematics, the semi-implicit Euler method, also called symplectic Euler, semi-explicit Euler, Euler–Cromer, and Newton–Størmer–Verlet , is a modification of the Euler method for solving Hamilton's equations, a system of ordinary differential equations that arises in classical mechanics...
Euler's summation formula, a theorem about integrals.
Euler–Cauchy equation (or Euler equation), a second-order linear differential equation
Euler–Maclaurin formula – relation between integrals and sums

Geometry and spatial arrangement

Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...

defining a rotation in space.
Euler brick
Euler brick
In mathematics, an Euler brick, named after Leonhard Euler, is a cuboid whose edges and face diagonals all have integer lengths. A primitive Euler brick is an Euler brick whose edge lengths are relatively prime.- Properties :...
Euler's line
Euler's line
In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral; it passes through several important points determined from the triangle...

– relation between triangle center
Triangle center
In geometry a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles. For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of...

s
Euler operator
Euler operator
In mathematics, Euler operators are a small set of functions to create polygon meshes. They are closed and sufficient on the set of meshes, and they are invertible.- Purpose :...

– set of functions to create polygon meshes
Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
Euler squares, usually called Graeco-Latin square
Graeco-Latin square
In mathematics, a Graeco-Latin square or Euler square or orthogonal Latin squares of order n over two sets S and T, each consisting of n symbols, is an n×n arrangement of cells, each cell containing an ordered pair , where s is in S and t is in T, such that every row and every column contains...

s.
Euler's theorem in geometry
Euler's theorem in geometry
In geometry, Euler's theorem, named after Leonhard Euler, states that the distance d between the circumcentre and incentre of a triangle can be expressed as d^2=R \,...

, relating the circumcircle and incircle of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

.
Euler–Rodrigues formulas – concerns Euler–Rodrigues parameters and 3D rotation matrices

Graph theory

Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

and topological graph theory
Topological graph theory
In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....

, and the corresponding Euler's formula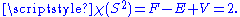
Eulerian circuit – (see Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

)
Euler class
Euler class
In mathematics, specifically in algebraic topology, the Euler class, named after Leonhard Euler, is a characteristic class of oriented, real vector bundles. Like other characteristic classes, it measures how "twisted" the vector bundle is...
Euler cycle – (see Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

)
Euler diagram
Euler diagram
An Euler diagram is a diagrammatic means of representing sets and their relationships. The first use of "Eulerian circles" is commonly attributed to Swiss mathematician Leonhard Euler . They are closely related to Venn diagrams....

– likely better (but wrongly) known as Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...

(which has more restrictions)
Euler's formula for planar graphs: v − e + f = 2
Eulerian graph – (see Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

)
Euler number (topology) – now, Euler characteristic
Eulerian path
Eulerian path
In graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...

, a path through a graph that takes each edge once.
Euler tour technique
Euler tour technique
The Euler tour technique , named after Leonhard Euler, is a method in graph theory for representing trees. The tree is viewed as a directed graph that contains two directed edges for each edge in the tree. The tree can then be represented as a Eulerian circuit of the directed graph, known as the...

Logarithms

Euler's number
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...

, e ≈ 2.71828, the base of the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

, also known as Napier's constant.
Euler–Mascheroni constant or Euler's constant γ ≈ 0.577216

Physical systems

Euler's Disk
Euler's disk
Euler's Disk is a scientific educational toy, used to illustrate and study the dynamic system of a spinning disk on a flat surface , and has been the subject of a number of scientific papers. This phenomenon has been studied since Leonard Euler in the 18th century, hence the name.It is manufactured...

– a toy consisting of a circular disk that spins, without slipping, on a surface
Euler equations in fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

.
Euler's equations, concerning the rotations of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...

.
Euler number (physics)
Euler number (physics)
The Euler number is a dimensionless number used in fluid flow calculations. It expresses the relationship between a local pressure drop e.g. over a restriction and the kinetic energy per volume, and is used to characterize losses in the flow, where a perfect frictionless flow corresponds to an...

, the cavitation number in fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

.
Euler's three-body problem
Euler's three-body problem
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are either fixed in space or move in circular coplanar orbits about their center of mass...
Euler–Bernoulli beam equation, concerning the elasticity of structural beams.
Euler formula
Buckling
In science, buckling is a mathematical instability, leading to a failure mode.Theoretically, buckling is caused by a bifurcation in the solution to the equations of static equilibrium...

in calculating the buckling load of columns.
Euler–Tricomi equation – concerns transonic flow

Polynomials

Euler's homogeneous function theorem, a theorem about homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...

s.
Euler polynomials
Euler spline – composed of classical Euler polynomial arcs (cred. to Schoenberg, 1973 – PDF)

Prime numbers

Euler's criterion
Euler's criterion
In mathematics, Euler's criterion is used in determining in number theory whether a given integer is a quadratic residue modulo a prime.-Definition:Euler's criterion states:Let p be an odd prime and a an integer coprime to p. Then...

– quadratic residues modulo by primes
Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...

– infinite product expansion, indexed by prime numbers of a Dirichlet series
Euler pseudoprime
Euler pseudoprime
In arithmetic, an odd composite integer n is called an Euler pseudoprime to base a, if a and n are coprime, and....
Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...

(or Euler phi (φ) function) in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, counting the number of coprime integers less than an integer.