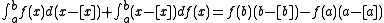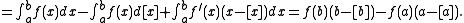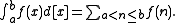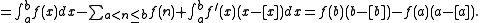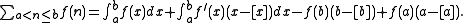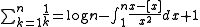Euler summation
Encyclopedia
Euler summation is a summability method for convergent and divergent series
. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series.
Euler summation can be generalized into a family of methods denoted (E, q), where q ≥ 0. The (E, 0) sum is the usual (convergent) sum, while (E, 1) is the ordinary Euler sum. All of these methods are strictly weaker than Borel summation; for q > 0 they are incomparable with Abel summation.
of alternating series and allows evaluating divergent sums.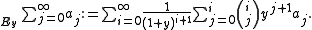
To justify the approach notice that for interchanged sum, Euler's summation reduces to the initial series, because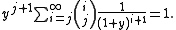
This method itself cannot be improved by iterated application, as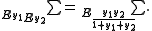
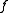 has a continuous derivative
has a continuous derivative 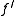 on
on 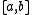 , then we have
, then we have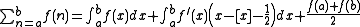
where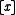 is the greatest integer which is less than or equal to
is the greatest integer which is less than or equal to  .
.
Proof: Applying the Riemann-Stieltjes integral
integration by parts, we have
Since the greatest-integer function has unit jumps at the integers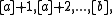 we can write
we can write
If we combine this fact with the previous equation, we have
Now we rearrange this equation to get the following
When and
and 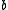 are integers, this becomes
are integers, this becomes
NOTE: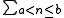 means the sum from
means the sum from 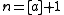 to
to 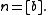
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series.
Euler summation can be generalized into a family of methods denoted (E, q), where q ≥ 0. The (E, 0) sum is the usual (convergent) sum, while (E, 1) is the ordinary Euler sum. All of these methods are strictly weaker than Borel summation; for q > 0 they are incomparable with Abel summation.
Definition
Euler summation is particularly used to accelerate the convergenceSeries acceleration
In mathematics, series acceleration is one of a collection of sequence transformations for improving the rate of convergence of a series. Techniques for series acceleration are often applied in numerical analysis, where they are used to improve the speed of numerical integration...
of alternating series and allows evaluating divergent sums.
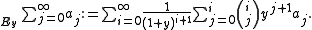
To justify the approach notice that for interchanged sum, Euler's summation reduces to the initial series, because
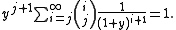
This method itself cannot be improved by iterated application, as
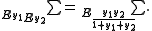
Examples
- We have
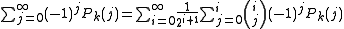 , if
, if  is a polynomial of degreeDegree of a polynomialThe degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
is a polynomial of degreeDegree of a polynomialThe degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
k. Note that in this case Euler summation reduces an infinite series to a finite sum.
- The particular choice
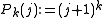 provides an explicit representation of the Bernoulli numbers, since
provides an explicit representation of the Bernoulli numbers, since 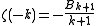 . Indeed, applying Euler summation to the zeta function yields
. Indeed, applying Euler summation to the zeta function yields 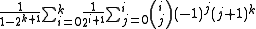 , which is polynomial for
, which is polynomial for 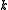 a positive integer; cf. Riemann zeta function.
a positive integer; cf. Riemann zeta function.
-
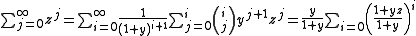 . With an appropriate choice of
. With an appropriate choice of 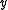 this series converges to
this series converges to 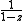 .
.
Definition
If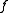 has a continuous derivative
has a continuous derivative 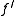 on
on 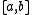 , then we have
, then we have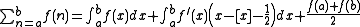
where
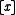 is the greatest integer which is less than or equal to
is the greatest integer which is less than or equal to  .
.Proof: Applying the Riemann-Stieltjes integral
Riemann-Stieltjes integral
In mathematics, the Riemann–Stieltjes integral is a generalization of the Riemann integral, named after Bernhard Riemann and Thomas Joannes Stieltjes.-Definition:...
integration by parts, we have
Since the greatest-integer function has unit jumps at the integers
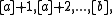 we can write
we can write
If we combine this fact with the previous equation, we have
Now we rearrange this equation to get the following
When
 and
and 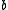 are integers, this becomes
are integers, this becomes
-
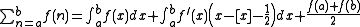 .
.
NOTE:
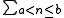 means the sum from
means the sum from 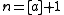 to
to 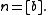
Examples
-
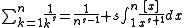 if
if 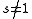
See also
- Borel summation
- Cesàro summationCesàro summationIn mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...
- Lambert summationLambert summationIn mathematical analysis, Lambert summation is a summability method for a class of divergent series.-Definition:A series \sum a_n is Lambert summable to A, written \sum a_n = A , if...
- Abelian and tauberian theoremsAbelian and tauberian theoremsIn mathematics, abelian and tauberian theorems are theorems giving conditions for two methods of summing divergent series to give the same result, named after Niels Henrik Abel and Alfred Tauber...
- Abel's summation formula
- Van Wijngaarden transformation