
Graeco-Latin square
Encyclopedia
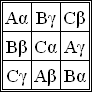
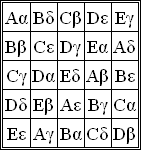
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
(s,t), where s is in S and t is in T, such that every row and every column contains each element of S and each element of T exactly once, and that no two cells contain the same ordered pair.
The arrangement of the Latin characters alone and of the Greek characters alone each forms a Latin square
Latin square
In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column...
. A Graeco-Latin square can therefore be decomposed into two "orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
" Latin squares. Orthogonality here means that every pair (s, t) from the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
S×T occurs exactly once.
History
Orthogonal Latin squares have been known to predate Euler. As described by Donald KnuthDonald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
in Volume 4 of TAOCP, the construction of 4x4 set was published by Jacques Ozanam in 1725 (in Recreation mathematiques et physiques) as a puzzle involving playing card
Playing card
A playing card is a piece of specially prepared heavy paper, thin cardboard, plastic-coated paper, cotton-paper blend, or thin plastic, marked with distinguishing motifs and used as one of a set for playing card games...
s. The problem was to take all aces, kings, queens and jacks from a standard deck of cards, and arrange them in a 4x4 grid such that each row and each column contained all four suits as well as one of each face value. This problem has several solutions.
A common variant of this problem was to arrange the 16 cards so that, in addition to the row and column constraints, each diagonal contains all four face values and all four suits as well. As described by Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
in Gardner's Workout, the number of distinct solutions to this problem was incorrectly estimated by Rouse Ball to be 72, and persisted many years before it was shown to be 144 by Kathleen Ollerenshaw
Kathleen Ollerenshaw
Dame Kathleen Mary Ollerenshaw, née Timpson, DBE is a British mathematician and politician. Deaf since the age of eight, she loved doing arithmetic problems as a child. As a young woman, she attended St Leonards School and Sixth Form College in St Andrews, Scotland where today the house of young...
. Each of the 144 solutions has 8 reflections and rotations, giving 1152 solutions in total. The 144x8 solutions can be categorized into the following two classes:
| Solution | Normal form |
|---|---|
| Solution #1 | |
| Solution #2 | |
For each of the two solutions, 24x24 = 576 solutions can be derived by permuting the four suits and the four face values independently. No permutation will convert the two solutions into each other.
The solution set can be seen to be complete through this proof outline:
- Without loss of generalityWithout loss of generalityWithout loss of generality is a frequently used expression in mathematics...
, let us choose the card in the top left corner to be . - Now, in the second row, the first two squares can be neither ace nor spades, due to being on the same column or diagonal respectively. Therefore, one of the remaining two squares must be an ace, and the other must be a spade, since the card itself cannot be repeated.
- If we choose the cell in the second row, third column to be an ace, and propagate the constraints, we will get Solution #1 above, up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a permutation of the remaining suits and face values. - Conversely, if we choose the (2,3) cell to be a spade, and propagate the constraints, we will get Solution #2 above, up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a permutation of the remaining suits and face values. - Since no other possibilities exist for (2,3), the solution set is complete.
Euler's work and conjecture
Orthogonal Latin squares were studied in detail by Leonhard EulerLeonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, who took the two sets to be S = {A, B, C, …}, the first n upper-case letters from the Latin alphabet
Latin alphabet
The Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...
, and T = {α , β, γ, …},
the first n lower-case letters from the Greek alphabet
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
—hence the name Graeco-Latin square.
In the 1780s Euler demonstrated methods for constructing Graeco-Latin squares where n is odd or a multiple of 4. Observing that no order-2 square exists and unable to construct an order-6 square (see thirty-six officers problem
Thirty-six officers problem
The thirty-six officers problem is a mathematical puzzle proposed by Leonhard Euler in 1782.The problem asks if it is possible to arrange 6 regiments consisting of 6 officers each of different ranks in a 6 × 6 square so that no rank or regiment will be repeated in any row or column. Such an...
), he conjectured that none exist for any oddly even number Indeed, the non-existence of order-6 squares was definitely confirmed in 1901 by Gaston Tarry
Gaston Tarry
Gaston Tarry was a French mathematician. Born in Villefranche de Rouergue, Aveyron, he studied mathematics at high school before joining the civil service in Algeria....
through exhaustive enumeration of all possible arrangements of symbols. However, Euler's conjecture resisted solution for a very long time.
Counterexamples to the conjecture of Euler
In 1959, R.C. BoseRaj Chandra Bose
Raj Chandra Bose was an Indian mathematician and statistician best known for his work in design theory and the theory of error-correcting codes in which the class of BCH codes is partly named after him. He was notable for his work along with S. S. Shrikhande and E. T...
and S. S. Shrikhande
S. S. Shrikhande
Sharadchandra Shankar Shrikhande is an Indian mathematician with distinguished and well-recognized achievements in combinatorial mathematics. He is notable for his breakthrough work along with R. C. Bose and E. T...
constructed some counterexamples (dubbed the Euler spoilers) of order 22 using mathematical insights. Then E. T. Parker
E. T. Parker
Ernest Tilden Parker is a professor emeritus from Ohio State University. He is notable for his breakthrough work along with R. C. Bose and S. S. Shrikhande in their disproof of the famous conjecture made by Leonhard Euler dated 1782 that there do not exist two mutually orthogonal latin squares of...
found a counterexample of order 10 through computer search on UNIVAC
UNIVAC
UNIVAC is the name of a business unit and division of the Remington Rand company formed by the 1950 purchase of the Eckert-Mauchly Computer Corporation, founded four years earlier by ENIAC inventors J. Presper Eckert and John Mauchly, and the associated line of computers which continues to this day...
(this was one of the earliest combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
problems solved on a digital computer).
In 1960, Parker, Bose, and Shrikhande showed Euler's conjecture to be false for all Thus, Graeco-Latin squares exist for all orders n ≥ 3 except
Applications
Graeco-Latin squares are used in the design of experimentsDesign of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
, tournament scheduling
Playoff format
There are several different Playoff formats used in various levels of competition in sports and games to determine an overall champion. Some of the most common are the single elimination, the best-of- series, the total points series, and the round-robin tournament.-Single elimination:A Single...
and constructing magic square
Magic square
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
s. The French writer Georges Perec
Georges Perec
Georges Perec was a French novelist, filmmaker, documentalist and essayist. He is a member of the Oulipo group...
structured his 1978 novel Life: A User's Manual
Life: A User's Manual
Life A User's Manual is Georges Perec's most famous novel, published in 1978, first translated into English by David Bellos in 1987. Its title page describes it as "novels", in the plural, the reasons for which become apparent on reading...
around a 10×10 orthogonal square.
Mutually orthogonal Latin squares
Mutually orthogonal Latin squares arise in various problems. A set of Latin squares is called mutually orthogonal if every pair of its element Latin squares is orthogonal to each other.| fjords | jawbox | phlegm | qiviut | zincky |
| zincky | fjords | jawbox | phlegm | qiviut |
| qiviut | zincky | fjords | jawbox | phlegm |
| phlegm | qiviut | zincky | fjords | jawbox |
| jawbox | phlegm | qiviut | zincky | fjords |
The above table shows 4 mutually orthogonal Latin squares of order 5, representing respectively:
- the text: fjordFjordGeologically, a fjord is a long, narrow inlet with steep sides or cliffs, created in a valley carved by glacial activity.-Formation:A fjord is formed when a glacier cuts a U-shaped valley by abrasion of the surrounding bedrock. Glacial melting is accompanied by rebound of Earth's crust as the ice...
s, jawboxJawboxJawbox was an alternative rock band from Washington, D.C., U.S.. Its original members were J. Robbins , Kim Coletta and Adam Wade...
, phlegmPhlegmPhlegm is a liquid secreted by the mucous membranes of mammalians. Its definition is limited to the mucus produced by the respiratory system, excluding that from the nasal passages, and particularly that which is expelled by coughing . Phlegm is in essence a water-based gel consisting of...
, qiviutQiviutQiviut is an Inuit word commonly used to indicate the wool of the muskox. The word was originally used to refer to the down feathers of birds as well as the inner wool of the muskox. It is valued for its use as a fiber as, unlike sheep's wool, it does not shrink in water at any temperature...
, and zincZincZinc , or spelter , is a metallic chemical element; it has the symbol Zn and atomic number 30. It is the first element in group 12 of the periodic table. Zinc is, in some respects, chemically similar to magnesium, because its ion is of similar size and its only common oxidation state is +2...
ky - the foreground color: white, red, lime, blue, and yellow
- the background color: black, maroon, teal, navy, and silver
- the typeface: serif (GeorgiaGeorgia (typeface)Georgia is a transitional serif typeface designed in 1993 by Matthew Carter and hinted by Tom Rickner for the Microsoft Corporation, as the serif companion to the first Microsoft sans serif screen font, Verdana. Microsoft released the initial version of the font on November 1, 1996 as part of the...
/ Times RomanTimes RomanTimes New Roman is a serif typeface commissioned by the British newspaper The Times in 1931, created by Victor Lardent at the English branch of Monotype. It was commissioned after Stanley Morison had written an article criticizing The Times for being badly printed and typographically antiquated...
), sans-serif (VerdanaVerdanaVerdana is a humanist sans-serif typeface designed by Matthew Carter for Microsoft Corporation, with hand-hinting done by Thomas Rickner, then at Monotype. Demand for such a typeface was recognized by Virginia Howlett of Microsoft's typography group...
/ HelveticaHelveticaHelvetica is a widely used sans-serif typeface developed in 1957 by Swiss typeface designer Max Miedinger with Eduard Hoffmann.-Visual distinctive characteristics:Characteristics of this typeface are:lower case:square dot over the letter i....
), monospace (Courier New), cursive (Comic SansComic SansComic Sans MS is a casual script typeface modeled on fonts used in American comic books for several decades. Sans is short for sans-serif. The modern Comic Sans was designed by Vincent Connare and released in 1994 by Microsoft Corporation...
), and fantasy (ImpactImpact (typeface)Impact is a realist sans-serif typeface designed by Geoffrey Lee in 1965 and released by the Stephenson Blake foundry. Its ultra-thick strokes, compressed letterspacing, and minimal interior counterform are specifically aimed, as its name suggests, to "impact". Impact has a high x-height, reaching...
).
Due to the Latin square property, each row and each column has all five texts, all five foregrounds, all five backgrounds, and all five typefaces.
Due to the mutually orthogonal property, there is exactly one instance somewhere in the table for any pair of elements, such as (white foreground, monospace), or (fjords, navy background) etc., and also all possible such pairs of values and dimensions are represented exactly once each.
The above table therefore allows for testing 5 values each of 4 different dimensions in only 25 observations instead of 625 observations. Note that the five 6-letter words (fjords, jawbox, phlegm, qiviut, and zincky) between them cover all 26 letters of the alphabet at least once each. The table therefore allows for examining each letter of the alphabet in five different typefaces, foreground colors, and background colors.
Due to a close relation between orthogonal Latin squares and combinatorial design
Combinatorial design
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
s, every pair of distinct cells in the 5x5 table will have exactly one of the following properties in common:
- a common row, or
- a common column, or
- a common text, or
- a common typeface, or
- a common background color, or
- a common foreground color.
In each category, every cell has 4 neighbors (4 neighbors in the same row with nothing else in common, 4 in the same column, etc.), giving 6 * 4 = 24 neighbors, which makes it a complete graph with 6 different edge colors.
The number of mutually orthogonal latin squares
The number of mutually orthogonal Latin squares that may exist for a given order n is not known for general n, and is an area of research in combinatoricsCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
. It is known that the maximum number of MOLS for any n cannot exceed (n-1), and this upper bound is achieved when n is a power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. The minimum is known to be 2 for all n except for n = 1, 2 or 6, where it is 1. For general composite numbers, the number of MOLS is not known. The first few values starting with n = 2, 3, 4... are 1, 2, 3, 4, 1, 6, 7, 8, ... .
See also
- Block design
- Blocking (statistics)Blocking (statistics)In the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups that are similar to one another. For example, an experiment is designed to test a new drug on patients. There are two levels of the treatment, drug, and placebo, administered to male...
- Combinatorial designCombinatorial designCombinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
- Design of experimentsDesign of experimentsIn general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
- Hyper-Graeco-Latin square designHyper-Graeco-Latin square designIn the design of experiments, hyper-Graeco-Latin squares are efficient designs to study the effect of one primary factor in the presence of 4 blocking factors. They are restricted, however, to the case in which all the factors have the same number of levels.Designs for 4- and 5-level factors are...
- Randomized block designRandomized block designIn the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups that are similar to one another. Typically, a blocking factor is a source of variability that is not of primary interest to the experimenter...
External links
- Euler's work on Latin Squares and Euler Squares at Convergence
- Java Tool which assists in constructing Graeco-Latin squares (it does not construct them by itself) at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Anything but square: from magic squares to Sudoku

