Pentagonal number theorem
Encyclopedia
In mathematics
, the pentagonal number theorem, originally due to Euler
, relates the product and series representations of the Euler function. It states that
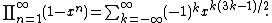
In other words,
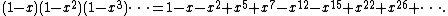
A striking feature of this expansion is the amount of cancellation in the product. The indices 1, 2, 5, 7, 12, ... appearing on the right hand side are called pentagonal numbers (or more accurately, generalized pentagonal numbers).
If we treat this series as a power series, the radius of convergence is 1. One may also ignore issues of convergence, in which case the theorem holds as a statement about formal power series
.
interpretation in terms of partitions. In particular, the left hand side is a generating function
for the number of partitions of n into an even number of distinct parts minus the number of partitions of n into an odd number of distinct parts. Each partition of n into an even number of distinct parts contributes +1 to the coefficient of xn; each partition into an odd number of distinct parts contributes −1. (The article on unrestricted partition functions discusses this type of generating function.)
For example, the coefficient of x5 is +1 because there are two ways to split 5 into an even number of distinct parts (4+1 and 3+2), but only one way to do so for an odd number of distinct parts (5 itself). However, the coefficient of x12 is −1 because there are seven ways to partition 12 into an even number of distinct parts, but there are eight ways to partition 12 into an odd number of distinct parts.
This interpretation leads to an elegant proof of the identity via involution. Consider the Ferrers graph of any partition of n into distinct parts. For example, the diagram below shows n = 20 and the partition 20 = 7 + 6 + 4 + 3.
>
If m > s, we take the rightmost 45 degree line and move it to form a new row, as in the graph below.
>
A bit of thought shows that applying the process twice will always bring us back to the original graph while also changing the parity of the number of rows. This enables us to pair off the Ferrers' graphs of partitions contributing 1 and -1 to the original sum (resulting in no net coefficient value for a particular power of x) except in those cases where this operation cannot be performed. There are two such cases:
1) m = s and the rightmost diagonal and bottom row meet. For example,
>
>
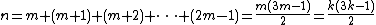
where k is taken to equal m. Note that the factor associated with this partion is (-1)s, which by construction equals (-1)m and (-1)k.
2) m = s+1 and the rightmost diagonal and bottom row meet. For example,
>
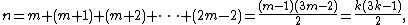
where m=1-k (which is negative). Here the associated factor is (-1)s with s = m-1 = -k, therefore the factor is also (-1)k.
In summary, we have shown that partitions into an even number of distinct parts and an odd number of distinct parts exactly cancel each other out, except for pentagonal number
s, where there is exactly one case left over. But this is precisely what the right side of the identity says should happen, so we are finished.
This gives a beautiful recurrence for calculating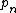
, the number of partitions of n Partition function (number theory).
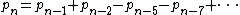
or more formally,
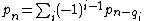
where the summation is over all (including negative) i and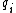
is the 
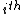pentagonal number calculated as above.
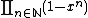is the exact inverse (in terms of formal power series) of the well known generating function for the partiton function p(n), 
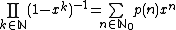. This means that
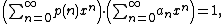
where an is the coefficient of xn in the expansion of our product. We thus have a0 p(0) = a0 = 1 and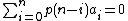
for all 
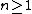(which, of course, is a recurrence relation that defines the ai uniquely). It is now easy to find an equivalence to our identity in terms of sets of partitions. Indeed, if we are to find
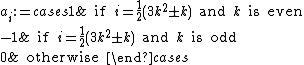
for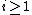
(which is what we want to prove), we need, substituting this formula into our above recurrence relation for ai, 
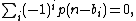(n > 0 as before) where 
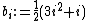and i ranges over all values such that 
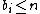(both positive and negative, as to encompass both kinds of generalized pentagonal numbers). This in turn means that
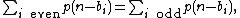
which transcribes in terms of sets of partitions as the fact that the sets
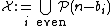and 
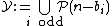
are of equal cardinality (using the same restrictions as before on i and n). All that remains to be done now is finding a bijection from one to the other and it is easy to check that the function φ from X to Y which maps the partition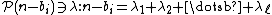
to the partiton 
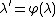where
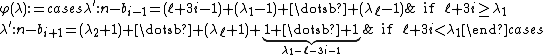
is actually an involution (and thus in particular a bijection), which proves our claim and the identity.
program which computes numbers of partitions using the Pentagonal number theorem.
pentagonal = lambda n : n*(3*n-1)/2
def generalised_pentagonal(n): # 0, 1, -1, 2, -2
if n < 0: return 0
if n%2 0: return pentagonal(n/2+1)
0: f = -f
r += f*pt[n - k]
i += 1
pt.append(r)
print pt
Q-series generalizes Euler's function, which is closely related to the Dedekind eta function
, and occurs in the study of modular forms. The modulus of the Euler function (see Q-series for picture) shows the fractal
modular group
symmetry and occurs in the study of the interior of the Mandelbrot set
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the pentagonal number theorem, originally due to Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, relates the product and series representations of the Euler function. It states that
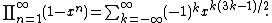
In other words,
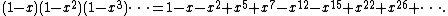
A striking feature of this expansion is the amount of cancellation in the product. The indices 1, 2, 5, 7, 12, ... appearing on the right hand side are called pentagonal numbers (or more accurately, generalized pentagonal numbers).
If we treat this series as a power series, the radius of convergence is 1. One may also ignore issues of convergence, in which case the theorem holds as a statement about formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
.
A combinatorial proof
The theorem can be given a combinatorialCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
interpretation in terms of partitions. In particular, the left hand side is a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the number of partitions of n into an even number of distinct parts minus the number of partitions of n into an odd number of distinct parts. Each partition of n into an even number of distinct parts contributes +1 to the coefficient of xn; each partition into an odd number of distinct parts contributes −1. (The article on unrestricted partition functions discusses this type of generating function.)
For example, the coefficient of x5 is +1 because there are two ways to split 5 into an even number of distinct parts (4+1 and 3+2), but only one way to do so for an odd number of distinct parts (5 itself). However, the coefficient of x12 is −1 because there are seven ways to partition 12 into an even number of distinct parts, but there are eight ways to partition 12 into an odd number of distinct parts.
This interpretation leads to an elegant proof of the identity via involution. Consider the Ferrers graph of any partition of n into distinct parts. For example, the diagram below shows n = 20 and the partition 20 = 7 + 6 + 4 + 3.
>
If m > s, we take the rightmost 45 degree line and move it to form a new row, as in the graph below.
>
A bit of thought shows that applying the process twice will always bring us back to the original graph while also changing the parity of the number of rows. This enables us to pair off the Ferrers' graphs of partitions contributing 1 and -1 to the original sum (resulting in no net coefficient value for a particular power of x) except in those cases where this operation cannot be performed. There are two such cases:
1) m = s and the rightmost diagonal and bottom row meet. For example,
>
>
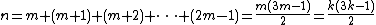
where k is taken to equal m. Note that the factor associated with this partion is (-1)s, which by construction equals (-1)m and (-1)k.
2) m = s+1 and the rightmost diagonal and bottom row meet. For example,
>
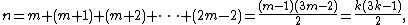
where m=1-k (which is negative). Here the associated factor is (-1)s with s = m-1 = -k, therefore the factor is also (-1)k.
In summary, we have shown that partitions into an even number of distinct parts and an odd number of distinct parts exactly cancel each other out, except for pentagonal number
Pentagonal number
A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon, but, unlike the first two, the patterns involved in the construction of pentagonal numbers are not rotationally symmetrical...
s, where there is exactly one case left over. But this is precisely what the right side of the identity says should happen, so we are finished.
This gives a beautiful recurrence for calculating
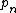, the number of partitions of n Partition function (number theory).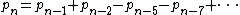or more formally,
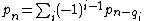
where the summation is over all (including negative) i and
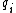is the 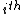pentagonal number calculated as above.A proof by bijection
Another way of proving the identity is by observing its implications on certain sets of partitions. Start by noting that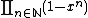 is the exact inverse (in terms of formal power series) of the well known generating function for the partiton function p(n), 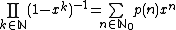. This means that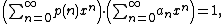where an is the coefficient of xn in the expansion of our product. We thus have a0 p(0) = a0 = 1 and
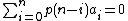for all 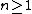(which, of course, is a recurrence relation that defines the ai uniquely). It is now easy to find an equivalence to our identity in terms of sets of partitions. Indeed, if we are to find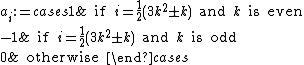for
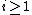(which is what we want to prove), we need, substituting this formula into our above recurrence relation for ai, 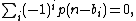(n > 0 as before) where 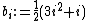and i ranges over all values such that 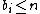(both positive and negative, as to encompass both kinds of generalized pentagonal numbers). This in turn means that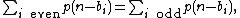which transcribes in terms of sets of partitions as the fact that the sets
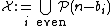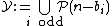
and are of equal cardinality (using the same restrictions as before on i and n). All that remains to be done now is finding a bijection from one to the other and it is easy to check that the function φ from X to Y which maps the partition
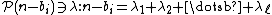to the partiton 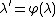where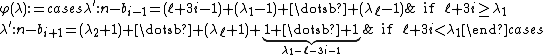is actually an involution (and thus in particular a bijection), which proves our claim and the identity.
Example program
Here is a simple PythonPython (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
program which computes numbers of partitions using the Pentagonal number theorem.
pentagonal = lambda n : n*(3*n-1)/2
def generalised_pentagonal(n): # 0, 1, -1, 2, -2
if n < 0: return 0
if n%2
0: return pentagonal(n/2+1)
else: return pentagonal(-(n/2+1))
pt = [1]
for n in range (1, 1000+1):
r = 0
f = -1
i = 0
while 1:
k = generalised_pentagonal(i)
if k > n:
break
if i%2
0: f = -fr += f*pt[n - k]
i += 1
pt.append(r)
print pt
See also
The pentagonal number theorem occurs as a special case of the Jacobi triple product.Q-series generalizes Euler's function, which is closely related to the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
, and occurs in the study of modular forms. The modulus of the Euler function (see Q-series for picture) shows the fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
symmetry and occurs in the study of the interior of the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
.
External links
- On Euler's Pentagonal Theorem at MathPages, the partition numbers.