
List of operators
Encyclopedia
In mathematics
, an operator or transform
is a function
from one space of functions
to another. Operators occur commonly in engineering
, physics
and mathematics. Many are integral operators and differential operator
s.
In the following L is an operator
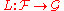
which takes a function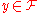 to another function
to another function  . Here,
. Here, 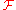 and
and 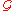 are some unspecified function space
are some unspecified function space
s, such as Hardy space
, Lp space
, Sobolev space
, or, more vaguely, the space of holomorphic function
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an operator or transform
Transformation (mathematics)
In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.Examples include...
is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from one space of functions
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
to another. Operators occur commonly in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics. Many are integral operators and differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s.
In the following L is an operator
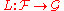
which takes a function
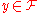 to another function
to another function  . Here,
. Here, 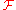 and
and 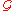 are some unspecified function space
are some unspecified function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, such as Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
, Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
, or, more vaguely, the space of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s.
| Expression | Curve definition |
Variables | Description |
|---|---|---|---|
| Linear transformations | |||
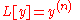 |
Derivative of nth order | ||
 |
Cartesian | 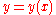  |
Integral, area |
 |
Composition operator Composition operator In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the ruleC_\phi = f \circ\phiwhere f \circ\phi denotes function composition. In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman... |
||
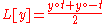 |
Even component | ||
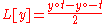 |
Odd component | ||
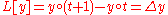 |
Difference operator | ||
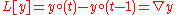 |
Backward difference (Nabla operator) | ||
 |
Indefinite sum operator (inverse operator of difference) | ||
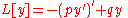 |
Sturm–Liouville operator | ||
| Non-linear transformations | |||
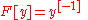 |
Inverse function Inverse function In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x... |
||
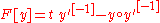 |
Legendre transformation Legendre transformation In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another... |
||
 |
Left composition | ||
 |
Indefinite product | ||
 |
Geometric integral | ||
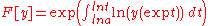 |
Bigeometric integral | ||
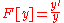 |
Logarithmic derivative Logarithmic derivative In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f.... |
||
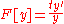 |
Elasticity | ||
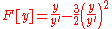 |
Schwarzian derivative Schwarzian derivative In mathematics, the Schwarzian derivative, named after the German mathematician Hermann Schwarz, is a certain operator that is invariant under all linear fractional transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and... |
||
 |
Geometric derivative | ||
 |
Bigeometric derivative | ||
| Total variation Total variation In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure... |
|||
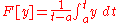 |
Arithmetic mean | ||
 |
Geometric mean | ||
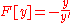 |
Cartesian | 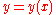  |
Subtangent Subtangent In geometry, the subtangent and related terms are certain line segments defined using the line tangent to a curve at a given point and the coordinate axes... |
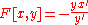 |
Parametric Cartesian |
 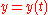 |
|
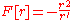 |
Polar |   |
|
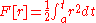 |
Polar | 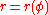  |
Sector area |
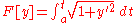 |
Cartesian | 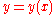  |
Arc length Arc length Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves... |
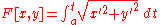 |
Parametric Cartesian |
 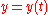 |
|
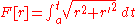 |
Polar | 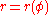  |
|
 |
Cartesian | 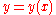  |
Affine arc length Affine curvature Special affine curvature, also known as the equi-affine curvature or affine curvature, is a particular type of curvature that is defined on a plane curve that remains unchanged under a special affine transformation . The curves of constant equi-affine curvature k are precisely all non-singular... |
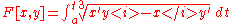 |
Parametric Cartesian |
 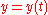 |
|
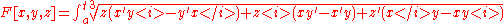 |
Parametric Cartesian |
 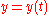  |
|
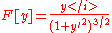 |
Cartesian | 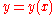  |
Curvature Curvature In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context... |
 |
Parametric Cartesian |
 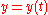 |
|
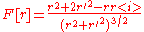 |
Polar |   |
|
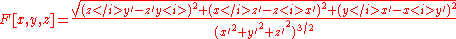 |
Parametric Cartesian |
 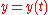  |
|
 |
Cartesian |   |
Affine curvature Affine curvature Special affine curvature, also known as the equi-affine curvature or affine curvature, is a particular type of curvature that is defined on a plane curve that remains unchanged under a special affine transformation . The curves of constant equi-affine curvature k are precisely all non-singular... |
 |
Parametric Cartesian |
 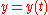 |
|
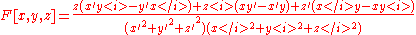 |
Parametric Cartesian |
 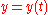  |
Torsion of curves Torsion of curves In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting. Taken together,the curvature and the torsion of a space curve are analogous to the curvature of a plane curve... |
 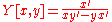 |
Parametric Cartesian |
 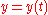 |
Dual curve Dual curve In projective geometry, a dual curve of a given plane curve C is a curve in the dual projective plane consisting of the set of lines tangent to C. There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If C is algebraic then so is its dual and the degree... (tangent coordinates) |
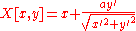  |
Parametric Cartesian |
 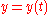 |
Parallel curve |
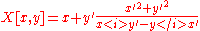 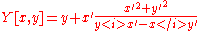 |
Parametric Cartesian |
  |
Evolute Evolute In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve.... |
 |
Intrinsic |   |
|
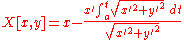 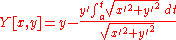 |
Parametric Cartesian |
 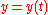 |
|Involute Involute In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight... |
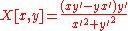 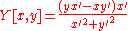 |
Parametric Cartesian |
 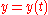 |
|Pedal curve Pedal curve In the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve .... with pedal point (0;0) |
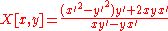  |
Parametric Cartesian |
 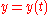 |
|Negative pedal curve Negative pedal curve In the plane, for every point X other than P there is a unique line through X perpendicular to XP. For a given curve in the plane and a given fixed point P, called the pedal point, the negative pedal curve is the envelope of the lines XP for which X lies on the given curve.The negative pedal curve... with pedal point (0;0) |
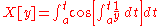  |
Intrinsic | 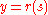  |
Intrinsic to Cartesian transformation |
| Metric functionals | |||
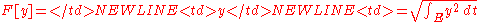 |
Norm Norm (mathematics) In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector... |
||
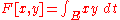 |
Inner product | ||
 |
Fubini-Study metric Fubini-Study metric In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study.... (inner angle) |
||
| Distribution functionals | |||
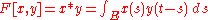 |
Convolution Convolution In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation... |
||
 |
Differential entropy Differential entropy Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:... |
||
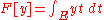 |
Expected value Expected value In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on... |
||
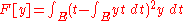 |
Variance Variance In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution... |
||
See also
- List of transforms
- List of Fourier-related transforms
- Transfer operatorTransfer operatorIn mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
- Fredholm operatorFredholm operatorIn mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
- Borel transform
- Table of mathematical symbolsTable of mathematical symbolsThis is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...

